6. ３次元形状を作る～直方体（２）

MATLABでアニメーション作成

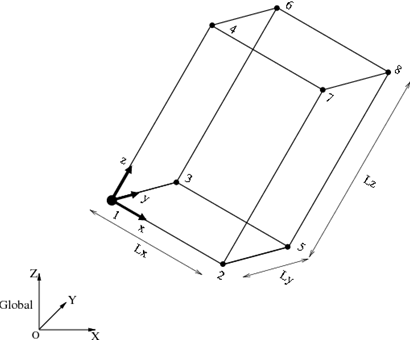
図１のような一般配置の直方体は、一角に張り付いた形状基準枠の位置と回転姿勢および３辺の長さ（Lx, Ly, Lz）で定義できます。形状基準枠の位置座標ベクトルを r 、回転行列を R とすれば、頂点の座標は次の式で求まります。

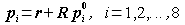
ここで p⁰_i は基本配置における頂点の座標です。頂点の座標が求まれば、前項と同様に patch で６個の面を作成して直方体を作ることができます。

図１：直方体（一般配置）

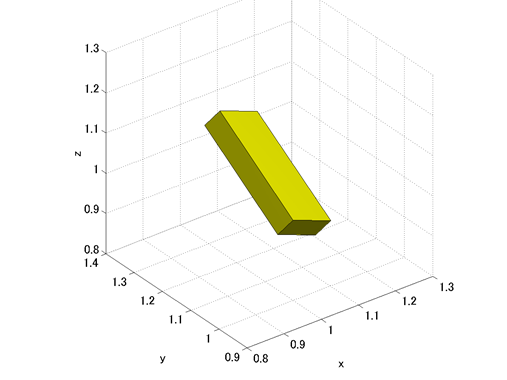
一般配置の直方体を作成するMATLABスクリプトをコード１に、このスクリプトによる描画の結果を図２にそれぞれ示します。スクリプト中で使用されている関数 eulerXYZ() は、XYZオイラー角を回転行列に変換する関数で、コード２のように定義されます。

make_block_general.m

% make_block_general.m

clear; close all;

% Reference position
r = [1; 1; 1];

% Reference orientation
R = eulerXYZ(-pi/3, 0, pi/6);

% Side lengths
Lx = 0.15;
Ly = 0.05;
Lz = 0.30;

% Vertices
vertices_0 = [
    0,   0,  0;  % #1
    Lx,  0,  0;  % #2
    0,  Ly,  0;  % #3
    0,   0, Lz;  % #4
    Lx, Ly,  0;  % #5
    0,  Ly, Lz;  % #6
    Lx,  0, Lz;  % #7
    Lx, Ly, Lz]; % #8

vertices = r' + vertices_0*R';

% Faces
faces = [
    1, 2, 5, 3;  % #1
    1, 3, 6, 4;  % #2
    1, 4, 7, 2;  % #3
    4, 7, 8, 6;  % #4
    2, 5, 8, 7;  % #5
    3, 6, 8, 5]; % #6

% Draw patch
figure(1);
h = patch('Faces', faces, 'Vertices', vertices, 'FaceColor', 'y');

% Axes settings
xlabel('x'); ylabel('y'); zlabel('z');
axis vis3d equal;
view([-37.5, 30]);
camlight;
grid on;
xlim([0.8, 1.3]);
ylim([0.9, 1.4]);
zlim([0.8, 1.3]);

コード１：直方体を作成するMATLABスクリプト（一般配置）

eulerXYZ.m

function R = eulerXYZ(a1, a2, a3)
% Convert XYZ Euler angles to rotation matrix

R1 = [
    1, 0, 0;
    0, cos(a1), -sin(a1);
    0, sin(a1), cos(a1)];

R2 = [
    cos(a2), 0, sin(a2);
    0, 1, 0;
    -sin(a2), 0, cos(a2)];

R3 = [
    cos(a3), -sin(a3), 0;
    sin(a3), cos(a3), 0;
    0, 0, 1];

R = R1*R2*R3;

end

コード２： XYZオイラー角を回転行列に変換するMATLAB関数

図２：６個の面を組み合わせて作成した直方体（一般配置）

<< 5. ３次元形状を作る～直方体（１）

>> 7. ３次元形状を作る～円柱（１）

MATLABでアニメーション作成・目次