前項の続きで、例題1の入力ファイル「free_falling_body.mbd」のnodesブロックとelementsブロックの内容について解説します。ここでは、MBDynでシミュレーションモデルを構築する上で最も基本となる、“structural node”と“body”要素が登場します。
nodeとは、シミュレーションモデルの自由度の担い手であり、シミュレーションモデルを構築する上で欠かせない要素です。 nodeには次のような種類があります。
この中で、剛体の自由度(6自由度)を担うことができるのはstructural nodeです。例題1では、1つの剛体の運動を扱うので、structural nodeを空間内に1つ定義する必要があります。もし剛体が2つならば2つのstructural nodeが必要となり、一般にN個の剛体の運動をシミュレーションする際にはN個のstructural nodeが必要となります。structural nodeにはstatic、dynamic、modal、dummyの4つの形態(type)がありますが、運動する剛体の自由度を担わせる用途においては、dynamicを選択します。
dynamicなstructural nodeを定義する基本的なステートメントの型は次のようになります。
structural: <node label>, dynamic, <position>, <orientation>,
<velocity>, <angular velocity> ;
さて、例題1の入力ファイルのnodesブロックでは、1つのstructural nodeが定義されています。
structural: 1, dynamic, null, eye, 0., 3., 0., null;
これを上記の型と対応させると、以下のようになります。
つまり、このdynamicなstructural nodeには「1」というラベル(名前)が付けられ、初期位置は「null」(=[0.,0.,0.])、初期姿勢は「eye」(単位行列)、初期速度は「0., 3., 0.」(Y方向に3.0)、初期角速度は「null」(=[0.,0.,0.])となります。剛体の初期速度を、このstructural nodeの初期速度に反映させている点に注目しましょう。
一般に、<node label>は整数、<position>、<velocity>、<angular velocity>は3次元ベクトル(3×1ベクトル)、<orientation>は3×3回転行列で指定します。また、零ベクトルは「null」、単位行列は「eye」というキーワードで代用することが可能です。
3次元ベクトルは一般に、単に数字を3つ並べれば良いので簡単ですが、eye以外の3×3回転行列は一般にどのように記述すれば良いのでしょうか?いくつか方法がありますが、最も単純な方法は、「matr」というキーワードに続いて9個の行列要素を行順に羅列する方法です。例えば、Z軸周り45度の回転を表す回転行列
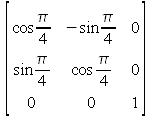
は、次のように記述できます。
matr, cos(pi/4.), -sin(pi/4.), 0., sin(pi/4.), cos(pi/4.), 0., 0., 0., 1.,
ちなみに、eyeは
matr, 1., 0., 0., 0., 1., 0., 0., 0., 1.,
と同義です。行列や回転行列を記述する色々な方法については第13項で紹介します。
structural nodeは剛体の自由度を与えるだけなので、それだけでは剛体を定義したことにはなりません。剛体を定義するためには、質量、重心位置、および慣性テンソルの情報が必要です。これらの情報を担うのがbodyと呼ばれる要素で、elementsブロック内で定義します。
bodyを定義する基本的なステートメントの型は次のようになります。
body: <label>, <node label>, <mass>, <relative center of mass>,
<inertia matrix> ;
さて、例題1の入力ファイルのelementsブロックでは、1つのbodyが定義されています。
body: 1, 1, 1., null, eye;
これを上記の型と対応させると、以下のようになります。
つまり、このbodyには「1」というラベルが付けられ、ラベル「1」のnodeにくっつきます。また、質量は「1.」、nodeに対する重心の相対位置は「null」(=[0.,0.,0.])、慣性行列は「eye」(単位行列)となります。
一般に、<label>は整数、<node label>は存在するnodeのラベル(整数)、<mass>は実数、<relative center of mass>は3次元ベクトル(3×1ベクトル)、<inertia matrix>は3×3行列で指定します。また、零ベクトルは「null」、単位行列は「eye」というキーワードで代用することが可能です。
最後は、重力を定義するステートメントです。
gravity: 0., 0., -1., const, 9.81;
これは、おそらく簡単に予想できるように、「0., 0., -1.」で重力の方向(−Z方向)を定め、「const, 9.81」で重力加速度の大きさ(定数)を定義しています。正確には、gravityカードの引数はtemplate drive caller(第19項参照)と呼ばれるオブジェクトで、上記ステートメントは実は、次のステートメントの省略形です。
gravity: single, 0., 0., -1., const, 9.81;
