A great advantage of computational analyses is that we can easily make an experiment on a model. To illustrate this let us make one dynamics experiment.
As can be seen from the animations of Case 1 and Case 2 in the last chapter, when a rigid body rotates about a principal axis of inertia, the axis of rotation remains fixed. But if the axis of rotation gets off the principal axis even slightly, the axis of rotation sways and no longer remains fixed.
Now, consider a rigid body rotating about a principal axis and suppose that the axis of rotation gets off the principal axis slightly. Then, if the axis of rotation remains in the vicinity of the principal axis, the rotational motion about the principal axis is said to be stable. If, on the other hand, the axis of rotation deviates largely, the rotational motion about the principal axis is said to be unstable.
Theoretically, it is known that the rotation about the principal axis corresponding to either the largest or the smallest moment of inertia is stable and the rotation about the principal axis corresponding to the intermediate moment of inertia is unstable. For the block in our current example problem, since Iyy > Ixx > Izz, the rotation about the principal axis corresponding to either the Y or the Z axis is stable and the rotation about the principal axis corresponding to the X axis is unstable. Let's test this theoretical inference with simulations.
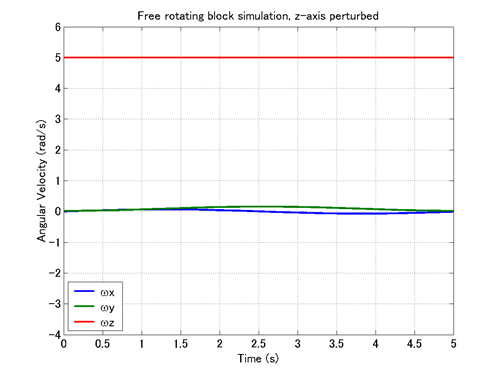
First, we conduct a simulation to test the stability of the rotation about the Z-axis. We use the input file "free_rotating_block.mbd" given in the last chapter with the following initial angular velocity.
Wx0=0., Wy0=0.02, Wz0=5. (rad/s)
This initial angular velocity involves a very small perturbing Y-component as well as the major Z-component.
Movie 1 shows an animation of the simulation result and Figure 1 shows the variation of the angular velocity with respect to time. A MATLAB script to draw the graph of Figure 1 is given in Code 1. From Movie 1 and Figure 1 we can see that in spite of a small stir, the axis of rotation is kept in the vicinity of the Z-axis. This result supports the theoretical inference that the rotation about the Z-axis is stable.
% plot_angular_velocity.m
clear; close all;
M=dlmread('free_rotating_block.mov');
wx=M(:,11); wy=M(:,12); wz=M(:,13);
t=1.e-2*[0:length(wx)-1]';
plot(t,wx,t,wy,t,wz,'LineWidth',2);
grid on;
xlim([0,5]);
ylim([-4,6]);
set(gca,'FontSize',14);
xlabel('Time (s)','FontSize',14);
ylabel('Angular Velocity (rad/s)','FontSize',14);
title('Free rotating block simulation','FontSize',14)
legend('\omega{x}','\omega{y}','\omega{z}',3);
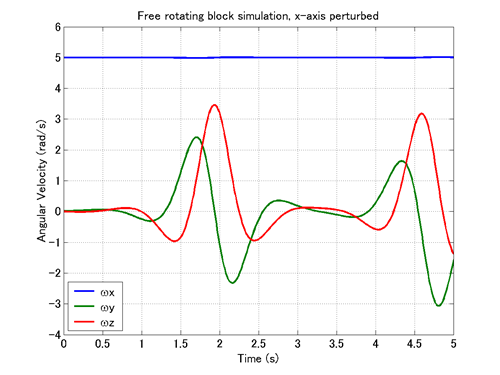
Next, let us conduct a simulation to test the instability of the rotation about the X-axis. We use the input file "free_rotating_block.mbd" with the following initial angular velocity.
Wx0=5., Wy0=0.02, Wz0=0. (rad/s)
This initial angular velocity involves a very small perturbing Y-component as well as the major X-component.
Movie 2 shows an animation of the simulation result and Figure 2 shows the variation of the angular velocity with respect to time. From Movie 2 and Figure 2, we can see that the initially small stir of the axis of rotation grows with time and the axis of rotation deviates largely from the X-axis. From this result we can confirm that the rotation about the X-axis is indeed unstable.