コンピュータ解析の大きな利点の一つは、「手軽に実験ができる」ことです。そこで、前項で作成した自由回転するブロックのシミュレーションモデルを用いて、力学実験を一つ行ってみましょう。
前項でシミュレーションを行ったケース1とケース2のアニメーションでも見られるように、剛体が慣性主軸周りに自由回転する時、回転軸は常に一定に保たれます。しかし、回転軸が慣性主軸から少しでもずれると、回転軸は揺動し、一定ではなくなります。
さて、剛体が慣性主軸の周りに自由回転している時、回転軸が微小量だけ慣性主軸からずれたとします。この時、回転軸の揺動が微小量に保たれる場合、この慣性主軸周りの回転運動は安定であると言います。一方、回転軸のずれがどんどん大きくなってしまうような場合、この慣性主軸周りの回転運動は不安定であると言います。
理論的には、最大の主慣性モーメントを持つ慣性主軸と最小の主慣性モーメントを持つ慣性主軸の周りの回転運動は安定で、中間の主慣性モーメントを持つ慣性主軸の周りの回転運動は不安定であるとされています。本例題のブロックにおいては、Iyy > Ixx > Izz であるので、y軸とz軸に対応する慣性主軸周りの回転運動は安定、x軸に対応する慣性主軸周りの回転運動は不安定ということになります。これを、シミュレーションによる実験で確かめてみましょう。
まず、z軸周りの回転運動の安定性を確かめるシミュレーションを行ってみましょう。前項に示した入力ファイル「free_rotating_block.mbd」を用いて、次の初期角速度でシミュレーションを行います。
Wx0=0., Wy0=0.02, Wz0=5. (rad/s)
この初期角速度にはz軸周りの主成分に加え、微小なy軸周りの成分が入っています。
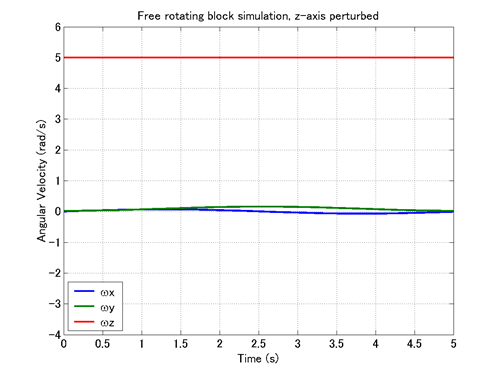
シミュレーション結果のアニメーションを動画1に、角速度の時間変化を表すグラフを図1に示します。また参考として、図1のグラフを描画するMATLABスクリプトをコード1に示します。動画1と図1より、微小な角速度の揺動はあるものの、回転軸はおおむねz軸近傍に保たれていることが分かります。この結果は、z軸周りの回転運動が安定であることを裏づけています。
% plot_angular_velocity.m
clear; close all;
M=dlmread('free_rotating_block.mov');
wx=M(:,11); wy=M(:,12); wz=M(:,13);
t=1.e-2*[0:length(wx)-1]';
plot(t,wx,t,wy,t,wz,'LineWidth',2);
grid on;
xlim([0,5]);
ylim([-4,6]);
set(gca,'FontSize',14);
xlabel('Time (s)','FontSize',14);
ylabel('Angular Velocity (rad/s)','FontSize',14);
title('Free rotating block simulation','FontSize',14)
legend('\omega{x}','\omega{y}','\omega{z}',3);
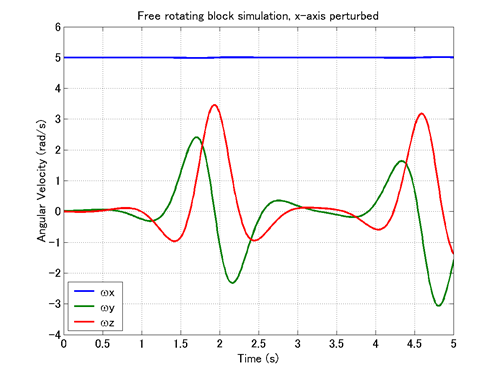
次に、x軸周りの回転運動の不安定性を確かめるシミュレーションを行ってみましょう。入力ファイル「free_rotating_block.mbd」を用いて、次の初期角速度でシミュレーションを行います。
Wx0=5., Wy0=0.02, Wz0=0. (rad/s)
この初期角速度にはx軸周りの主成分に加え、微小なy軸周りの成分が入っています。
シミュレーション結果のアニメーションを動画2に、角速度の時間変化を表すグラフを図2に示します。動画2と図2より、最初は微小な回転軸の揺動が時間とともにどんどん増加し、回転軸はx軸から大きく逸脱してしまうことが分かります。この結果から、x軸周りの回転運動が不安定であることが確かめられます。