In this chapter, we construct a simulation model of a spring-mass-damper system that is equivalent to the one in the previous chapter but using a "deformable displacement joint" instead of the structural internal force to express a spring-damper.
Joints usually add hard constraints on a system and decrease its degrees of freedom. But the following three "deformable" joints are exceptional.
As the name "deformable" suggests, these joints connect two nodes with elastic or viscous force. You may imagine a rubber piece that connects two rigid bodies. Deformable displacement joint can apply translational forces, deformable hinge can apply rotational forces (torques), and deformable joint can apply both translational and rotational forces. The properties such as elasticity and viscosity of deformable joints are defined by "constitutive law." Many constitutive laws are available. Refer to the official Input manual for details.
This joint can apply translational elastic and/or viscous forces between two nodes (or the points offset by <relative offset>). The basic syntax for the statement that defines a deformable displacement joint is as follows.
joint: <label>
deformable displacement joint,
<node 1>,
<relative offset 1>,
[ hinge, <relative orientation matrix 1>, ]
<node 2>,
<relative offset 2>,
[ hinge, <relative orientation matrix 2>, ]
<constitutive law>;
Here, <constitutive law> refers to the coordinate frame of node1.
Generally, a spring-damper can be expressed by a deformable displacement joint. In our current example problem, we define the deformable displacement joint as follows. (See also Figure 1)
set: integer JoDfmd_SpringDamper = 4;
joint: JoDfmd_SpringDamper,
deformable displacement joint,
Node_Ground,
null, # relative offset
Node_Mass,
null, # relative offset
linear viscoelastic isotropic,
K, # stiffness
C, # viscosity coefficient
prestrain, single, 0., 0., -1, const, L;
Here, we use "linear viscoelastic isotropic" constitutive law because our spring-damper is a linear one. Also, since the spring has the natural length L>0, we define it with the keyword "prestrain."
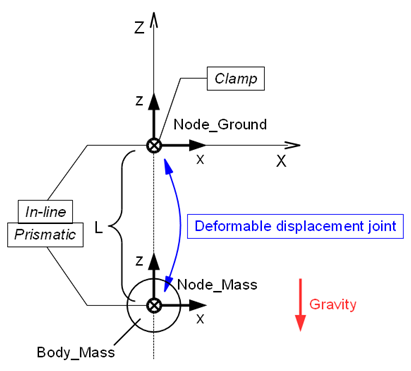
Code 1 shows an example input file of a spring-mass-damper system for Problem 8 in the case where a spring-damper is expressed by a deformable displacement joint.
# spring_mass_damper_2.mbd
#-----------------------------------------------------------------------------
# [Data Block]
begin: data;
problem: initial value;
end: data;
#-----------------------------------------------------------------------------
# [<Problem> Block]
begin: initial value;
initial time: 0.;
final time: 5.;
time step: 1.e-3;
max iterations: 10;
tolerance: 1.e-6;
end: initial value;
#-----------------------------------------------------------------------------
# [Control Data Block]
begin: control data;
skip initial joint assembly;
output frequency: 10;
structural nodes: 2;
rigid bodies: 1;
joints: 4;
gravity;
end: control data;
#-----------------------------------------------------------------------------
# Design Variables
set: real M = 1.; #[kg] Mass
set: real L = 1.; #[m] Spring Natural Length
set: real K = 20.; #[N/m] Spring Stiffness Coefficient
set: real C = 1; #[Ns/m] Damper Damping Coefficient
#-----------------------------------------------------------------------------
# Node Labels
set: integer Node_Ground = 1;
set: integer Node_Mass = 2;
# Body Labels
set: integer Body_Mass = 1;
# Joint Labels
set: integer JoClamp_Ground = 1;
set: integer JoInLin_Ground_Mass = 2;
set: integer JoPrism_Ground_Mass = 3;
set: integer JoDfmd_SpringDamper = 4;
#-----------------------------------------------------------------------------
# [Nodes Block]
begin: nodes;
#-----------------------------------------------------------------------------
# Nodes
structural: Node_Ground, static,
null, # absolute position
eye, # absolute orientation
null, # absolute velocity
null; # absolute angular velocity
structural: Node_Mass, dynamic,
0., 0., -L, # absolute position
eye, # absolute orientation
null, # absolute velocity
null; # absolute angular velocity
end: nodes;
#-----------------------------------------------------------------------------
# [Elements Block]
begin: elements;
#-----------------------------------------------------------------------------
# Bodies
body: Body_Mass, Node_Mass,
M, # mass
null, # relative center of mass
eye; # inertia matrix
#-----------------------------------------------------------------------------
# Joints
joint: JoClamp_Ground,
clamp,
Node_Ground,
null, # absolute position
eye; # absolute orientation
joint: JoInLin_Ground_Mass,
in line,
Node_Ground,
null, # relative line position
eye, # relative line orientation
Node_Mass;
joint: JoPrism_Ground_Mass,
prismatic,
Node_Ground,
Node_Mass;
joint: JoDfmd_SpringDamper,
deformable displacement joint,
Node_Ground,
null, # relative offset
Node_Mass,
null, # relative offset
linear viscoelastic isotropic,
K, # stiffness
C, # viscosity coefficient
prestrain, single, 0., 0., -1, const, L;
#-----------------------------------------------------------------------------
# Gravity
gravity: 0., 0., -1., const, 9.81;
end: elements;
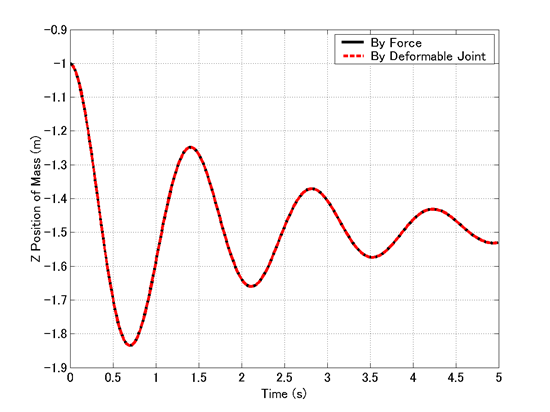
Figure 2 shows a comparison of the simulation results of the two spring-mass-damper models constructed in the previous chapter and this chapter using "structural internal force" and "deformable displacement joint." From this figure we can comfirm that the two models are actually equivalent.