In multibody dynamics analysis we often encounter cases where we need to express collisions or contacts between bodies. This chapter introduces a simple model that can express one-dimensional collisions and contacts.
Suppose a ball is flying toward a slab as depicted in Figure 1. The ball keeps approaching to the slab and will eventually be bounced off. Or if the speed of the ball is slow enough, the ball may stop after it reaches to the slab and rest on it afterward. How can we express the phenomena of bodies colliding and bouncing or the states of bodies in contacts like this in our simulation models?
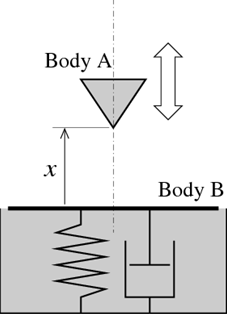
One simple method of modeling contacts is to express the contact force by a spring and a damper. Let the position of Body A relative to the contact surface of Body B be x as in Figure 2, then there is no force if x > 0 and a spring and damper force depending on x and dx/dt acts between Body A and B if x < 0.
The contact force acting on Body A can be expressed mathematically as follows.
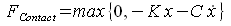
where K is the spring constant and C is the damping constant. Advantages of this contact model are that it can deal with collisions and contacts in a unified manner and it can be easily implemented because only one force definition is involved. There is a drawback, however, that at the time of collision a rough and discontinuous change of the force occurs and the convergence of numerical integration becomes deteriorated resulting in a large increase in the computational cost and in some cases a failure of the computation.
To alleviate the discontinuity problem, the model can be modified as follows.
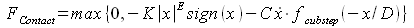
where E and D are constants and fcubstep(&sdot) is a function whose value changes smoothly from 0 to 1 as shown in Figure 3. In MBDyn the function fcubstep(&sdot) can be defined for example as follows.
scalar function: "cubstep",
cubicspline, do not extrapolate,
-0.03, 0.00,
-0.02, 0.00,
-0.01, 0.00,
0.00, 0.00,
1.00, 1.00,
1.01, 1.00,
1.02, 1.00,
1.03, 1.00;
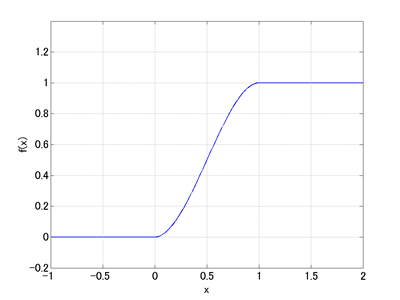
Figure 4 shows the graphs of the function y = - |x|E sign(x) with different values of E. From these graphs we can see that by setting the constant E to be larger than one the spring force at the time of collision becomes smoother. Meanwhile, by setting the constant D > 0 the damping force at the time of collision changes continuously from zero due to fcubstep(-x/D).
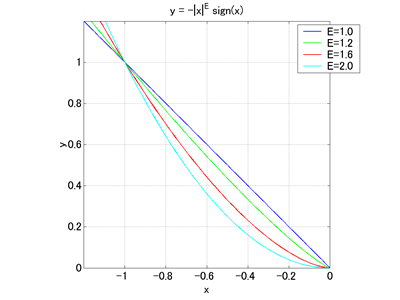
Despite the disadvantage in the computational cost, this spring-damper contact model is versatile and convenient. The values of the parameters K, C, E, and D are usually determined by considering both the precision and the computational cost of the simulation.
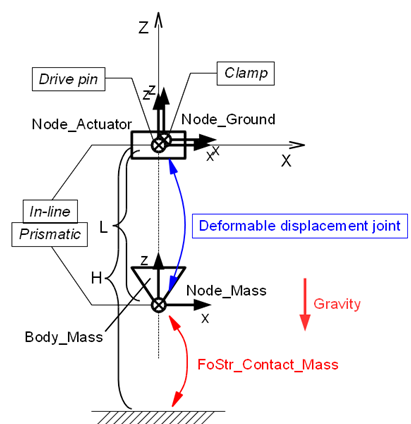
Movie 1 below is an animation of a simulation model that uses the contact model described above. This simulation model is obtained by partially modifying the simulation model for the spring-mass-damper system in Chapter 23. A motion input is added to the upper end of the spring and a contact force is applied between the mass and the ground. The plan of this simulation model is shown in Figure 1 and the input file is shown in Code 1.
# elastic_contact_1d.mbd
#-----------------------------------------------------------------------------
# [Data Block]
begin: data;
problem: initial value;
end: data;
#-----------------------------------------------------------------------------
# [<Problem> Block]
begin: initial value;
initial time: 0.;
final time: 4.;
time step: 1.e-3;
max iterations: 10;
tolerance: 1.e-7;
end: initial value;
#-----------------------------------------------------------------------------
# [Control Data Block]
begin: control data;
use: rigid bodies, gravity, in assembly;
output frequency: 10;
structural nodes: 3;
rigid bodies: 1;
joints: 5;
forces: 1;
gravity;
end: control data;
#-----------------------------------------------------------------------------
# Design Variables
set: real M = 1.; # Mass
set: real L = 1.; # Spring Natural Length
set: real K = 40.; # Spring Stiffness
set: real H = -1.5; # Table Position
set: real Kc = 10000.; # Contact Stiffness
set: real Ec = 1.2; # Contact Stiffness Exponent
set: real Cc = 10.; # Contact Damping
set: real Dc = 0.0001; # Contact Damping Activation Depth
#-----------------------------------------------------------------------------
# Node Labels
set: integer Node_Actuator = 1;
set: integer Node_Mass = 2;
set: integer Node_Ground = 3;
# Body Labels
set: integer Body_Mass = 1;
# Joint Labels
set: integer JoDrivp_Actuator = 1;
set: integer JoInlin_Actuator_Mass = 2;
set: integer JoPrism_Actuator_Mass = 3;
set: integer JoDfmd_Spring = 4;
set: integer JoClamp_Ground = 5;
# Force Labels
set: integer FoStr_Contact_Mass = 1;
#-----------------------------------------------------------------------------
# Scalar Functions
scalar function: "cubstep",
cubicspline, do not extrapolate,
-0.03, 0.00,
-0.02, 0.00,
-0.01, 0.00,
0.00, 0.00,
1.00, 1.00,
1.01, 1.00,
1.02, 1.00,
1.03, 1.00;
#-----------------------------------------------------------------------------
# [Nodes Block]
begin: nodes;
#-----------------------------------------------------------------------------
# Nodes
structural: Node_Actuator, dynamic,
null, # absolute position
eye, # absolute orientation
null, # absolute velocity
null; # absolute angular velocity
structural: Node_Mass, dynamic,
0., 0., -L, # absolute position
eye, # absolute orientation
null, # absolute velocity
null; # absolute angular velocity
structural: Node_Ground, static,
null, # absolute position
eye, # absolute orientation
null, # absolute velocity
null; # absolute angular velocity
end: nodes;
#-----------------------------------------------------------------------------
# Plugin Variables
set: [node, DZ, Node_Mass, structural, string="X[3]"];
set: [node, VZ, Node_Mass, structural, string="XP[3]"];
#-----------------------------------------------------------------------------
# [Elements Block]
begin: elements;
#-----------------------------------------------------------------------------
# Bodies
body: Body_Mass, Node_Mass,
M, # mass
null, # relative center of mass
eye; # inertia matrix
#-----------------------------------------------------------------------------
# Joints
joint: JoDrivp_Actuator,
drive displacement pin,
Node_Actuator,
null, # node offset
null, # offset
single, 0., 0., 1., sine, 1., pi/2., -1., one, 0.; # position
joint: JoInlin_Actuator_Mass,
in line,
Node_Actuator,
null, # relative line position
eye, # relative normal direction
Node_Mass;
joint: JoPrism_Actuator_Mass,
prismatic,
Node_Actuator,
Node_Mass;
joint: JoDfmd_Spring,
deformable displacement joint,
Node_Actuator,
null,
Node_Mass,
null,
linear elastic isotropic, K,
prestrain, single, 0., 0., -1, const, L;
joint: JoClamp_Ground,
clamp,
Node_Ground,
null, # absolute position
eye; # absolute orientation
#-----------------------------------------------------------------------------
# Forces
force: FoStr_Contact_Mass,
absolute,
Node_Mass,
position, null, # relative arm
single, 0., 0., 1.,
string, "max(0,Kc*sign(H-DZ)*abs(H-DZ)^Ec
-Cc*VZ*model::sf::cubstep((H-DZ)/Dc))"; # force value
#-----------------------------------------------------------------------------
# Gravity
gravity: 0., 0., -1., const, 9.81;
end: elements;
