本項では、MBDynの出力データの基本的な扱い方について説明します。
MBDynの計算結果は通常、いくつかの出力ファイルに書き出されます。例題1の入力ファイル「free_falling_body.mbd」を用いてMBDynを実行した場合には、次の4つの出力ファイルが自動的に作成されます。
これらの出力ファイルの内、拡張子が「out」と「log」のファイルには、実行されたシミュレーションに関する一般的な情報が書き出されます。また、拡張子が「mov」と「ine」のファイルには、シミュレーションによって得られた剛体の運動の時系列データが書き出されます。movファイルは剛体(structural node)の位置、姿勢、速度、および角速度のデータを含み、ineファイルは剛体の運動量、角運動量、およびそれらの時間微分のデータを含みます。
movファイル「free_falling_body.mov」のデータを表計算ソフトウェアで表示した様子を図1に示します。表計算ソフトウェアで表示したのは単に見やすくするためで、実際にはスペース区切りのテキストデータです。
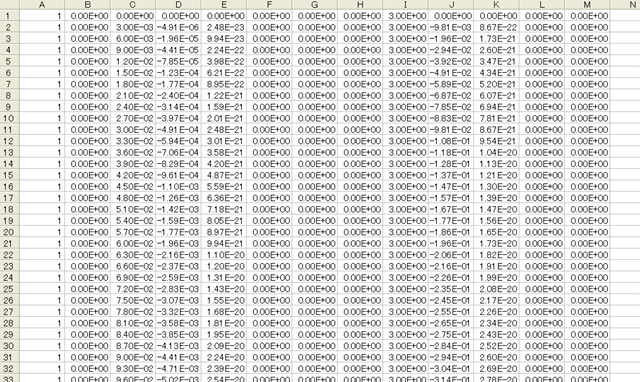
movファイルのデータは、次のように構成されます。
これらの量は基本的にグローバル座標系に対する量になっています。行の数はnode数と時間ステップ数の積になります。本例題の場合にはnodeが1つしかないので、各時間ステップにおいて1行のみの出力となっていますが、一般にN個のnodeがある場合には、各時間ステップでN行の出力があります。
姿勢(orientation)はxyzオイラー角と呼ばれる3つの角度の組で表されます。xyzオイラー角(α,β,γ)で表される姿勢とは、剛体に固定した座標系のx軸まわりにα、次いでy軸まわりにβ、次いでz軸まわりにγだけ回転することによって得られる姿勢です。xyzオイラー角(α,β,γ)と回転行列Rの関係は以下の式で与えられます。

ちなみに、movファイルに出力される姿勢の表現方法は、control dataブロック内で“default orientation”カードを用いて変更することができます。
default orientation: { euler123 | orientation vector | orientation matrix } ;
ここで、euler123はデフォルトのxyzオイラー角、orientation vectorは回転ベクトル、orientation matrixは回転行列による表現です。default orientationを変更すると、movファイル内で姿勢データが占める列数が変わるので、それに応じて速度や角速度のデータの列番号も変わることに注意する必要があります。
尚、movファイルには時間データは含まれていません。時間データが必要な場合には、入力ファイルのtime step等の設定に従って自ら作成するか、outファイルを参照します。
本チュートリアルでは、これ以降、出力データの処理はMATLABで行うこととして解説を進めて行きます。しかし、同様のデータ処理は、ScilabやOctaveなど他の汎用数値解析ソフトウェアを用いても行えます。他の汎用数値解析ソフトウェアを用いて出力データの処理を行う場合には、文中に示すMATLABのコードを随時読み替えて適用してください。
movファイルのデータはスペース区切りのテキストデータですので、例えばdlmreadコマンドを用いてMATLABにデータを読み込むことができます。
M = dlmread('free_falling_body.mov');
行列Mにはmovファイルのデータがそっくりそのまま入ります。従って、
x = M(:,2); y = M(:,3); z = M(:,4);
とすれば、node「1」の変位の各方向成分の時系列データをそれぞれ取り出すことができます。同様に
vx = M(:,8); vy = M(:,9); vz = M(:,10);
とすれば、速度の各方向成分の時系列データをそれぞれ取り出すことができます。(ただし、nodeが複数ある場合には、一列のデータの中に複数のnodeのデータが交互に織り込まれるので、nodeごとにデータを分離する処理がさらに必要になります。nodeが複数ある場合のデータ処理については、第11項で説明します。)
これらのデータを用いて様々なグラフを描画することができます。例えば、
plot(y,z)
と入力すれば、yz平面における剛体の軌跡を描くことができます。また、
plot3(x,y,z)
と入力すれば、3次元的に剛体の軌跡を見ることができます。
時間に対する変化をグラフに描くためには、時間データベクトルを作成する必要があります。入力ファイルを参照すれば、時刻0秒から1秒まで、時間刻み1e-3秒で結果が出力される設定になっているので、次のようにして時間データベクトルを作成します。
t = 0:1.e-3:1;
時間データベクトルを作成した後、次のように入力すれば、時間に対するy方向変位のグラフを描くことができます。
plot(t,y)
グラフを描画するだけでなく、データから様々な情報を引き出すことも時に必要となります。例えば、時刻0.1秒におけるz変位は次のように求められます。
z_01 = z(min(find(t>=0.1)));
また、z変位が-1になる時刻は次のように求めることができます。
t1 = t(min(find(z<-1)));
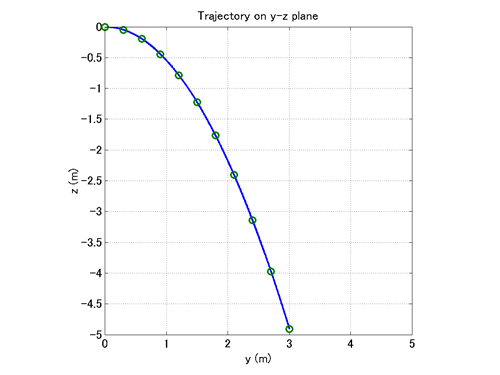
最後に参考として、yz平面における剛体の軌跡と0.1秒ごとの剛体の位置を示すグラフを描画するMATLABスクリプトをコード1に示します。また、そのスクリプトによって描かれるグラフを図2に示します。
% plot_trajectory.m
clear; close all;
M = dlmread('free_falling_body.mov');
x = M(:,2); y = M(:,3); z = M(:,4);
t = 0:1.e-3:1;
td = 0:0.1:1;
for k=1:length(td)
yd(k) = y(min(find(t>=td(k))));
zd(k) = z(min(find(t>=td(k))));
end
plot(y,z,'-',yd,zd,'o','LineWidth',2,'MarkerSize',8);
grid on;
axis([0,5,-5,0]);
axis square;
xlabel('y (m)','FontSize',14);
ylabel('z (m)','FontSize',14);
title('Trajectory on y-z plane','FontSize',14);
set(gca,'FontSize',14);