アニメーションの原理と、MBDynの出力データから剛体の運動のアニメーションを作成する方法について説明します。
まず、1次元の簡単なケースでアニメーションの原理を説明します。
ある点が時間とともにx軸上を移動するとします。一定時間間隔の点位置 x のデータが x = x1, x2, x3, ... と与えられている時、点の動きを表すアニメーションは次の1〜3を循環(ループ)させることによって作成することができます。ただし、点は小さな円で表示することとします。(図1参照)
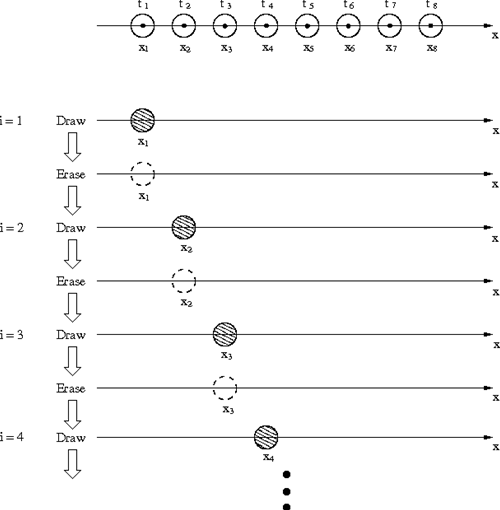
コード1に、移動する点のアニメーションを作成するMATLABスクリプトの例を示します。また、このスクリプトを実行して得られるアニメーションを動画1に示します。
% animation_point.m
clear; close all;
% Create data
t = 0:0.001:1; % Time data
x = sin(2*pi*t); % Position data
% Draw initial figure
figure(1);
set(gcf,'Renderer','OpenGL');
h = plot(x(1),0,'o','MarkerSize',20,'MarkerFaceColor','b');
set(h,'EraseMode','normal');
xlim([-1.5,1.5]);
ylim([-1.5,1.5]);
% Animation Loop
i = 1;
while i<=length(x)
set(h,'XData',x(i));
drawnow;
i = i+1;
end
剛体のアニメーションも、点のアニメーションと原理は全く同じです。剛体の場合、描画と消去の対象が3次元形状になるという違いがあるだけです。ただし、MBDynは剛体の運動をnodeという代表点の運動で記述するので、nodeのデータを3次元形状のデータに変換する手続きが必要になります。
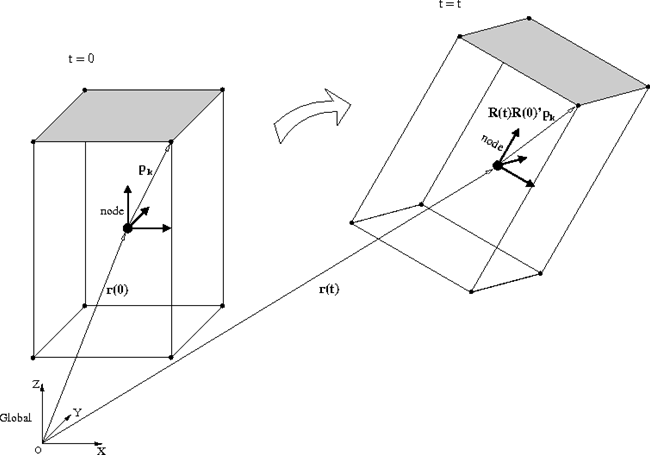
例として、図2のように剛体の形状がブロックの場合を考えてみましょう。まず、初期時刻におけるブロックの頂点を定義します(図2左)。ブロックの形状はnodeに張り付いて動くので、任意の時刻における頂点の座標は、nodeの位置と姿勢から図2右のように求めることができます。頂点の座標が求まれば、ブロックの形状を描画できます。このようにして、nodeの位置と姿勢のデータから各時刻におけるブロックの頂点の座標を求め、ブロックの形状に対して描画と消去のループを回せば、ブロックのアニメーションを表示することができます。
MATLABでは、一般の3次元形状を作成するのに“パッチ(patch)”が利用できます。パッチとは、3つ以上の点で定義される多角形の面です。パッチを組み合わせれば、任意の多面体を作ることができます。例えばブロック形状は、6個の四角形パッチを組み合わせて作ることができます。
さて、下のコード2は、例題2の自由回転するブロックの解析で出力されるmovファイルを読み込んで、ブロックの最上面のパッチのみをアニメーション表示するMATLABスクリプトです。動画2にこのスクリプトを実行して得られるアニメーションを示します。このようなパッチのアニメーションをブロックの6面全部について組み合わせれば、ブロックのアニメーションが完成します。
% animation_patch.m
clear; close all;
% Define Geometry Points (Vertices for the top surface of the block)
Lx = 0.15; %[m]
Ly = 0.05; %[m]
Lz = 0.30; %[m]
p1 = [ Lx/2, Ly/2, Lz/2 ];
p2 = [ Lx/2, -Ly/2, Lz/2 ];
p3 = [ -Lx/2, -Ly/2, Lz/2 ];
p4 = [ -Lx/2, Ly/2, Lz/2 ];
% Load Data
[LABEL,DATA] = MBDynLoad('free_rotating_block.mov');
r = DATA(:,[2:4],LABEL==1); % Node Position [m]
A = DATA(:,[5:7],LABEL==1)*pi/180; % Node Orientation [rad] (x-y-z Euler angle)
n = size(r,1); % Data Length
% Euler Angle -> Orientation Matrix
for i=1:n
a1 = A(i,1);
a2 = A(i,2);
a3 = A(i,3);
R1 = [1, 0, 0;
0, cos(a1), -sin(a1);
0, sin(a1), cos(a1)];
R2 = [cos(a2), 0, sin(a2);
0, 1, 0;
-sin(a2), 0, cos(a2)];
R3 = [cos(a3), -sin(a3), 0;
sin(a3), cos(a3), 0;
0, 0, 1];
R(:,:,i) = R1*R2*R3;
end
% Compute Propagation of Geometry Points
for i=1:n
r1(i,:) = r(i,:) + p1*R(:,:,1)*R(:,:,i)';
r2(i,:) = r(i,:) + p2*R(:,:,1)*R(:,:,i)';
r3(i,:) = r(i,:) + p3*R(:,:,1)*R(:,:,i)';
r4(i,:) = r(i,:) + p4*R(:,:,1)*R(:,:,i)';
end
% Compile Data for Drawing Patch
PatchData_X = [r1(:,1),r2(:,1),r3(:,1),r4(:,1)];
PatchData_Y = [r1(:,2),r2(:,2),r3(:,2),r4(:,2)];
PatchData_Z = [r1(:,3),r2(:,3),r3(:,3),r4(:,3)];
% Draw Initial Figure
figure(1);
set(gcf,'Renderer','OpenGL');
h = patch(PatchData_X(1,:),PatchData_Y(1,:),PatchData_Z(1,:),'y');
set(h,'EraseMode','normal');
axis vis3d equal;
view([-37.5,30]);
camlight;
grid on;
xlim([-0.2,0.2]);
ylim([-0.2,0.2]);
zlim([-0.2,0.2]);
% Animation Loop
for i=1:n
set(h,'XData',PatchData_X(i,:)');
set(h,'YData',PatchData_Y(i,:)');
set(h,'ZData',PatchData_Z(i,:)');
drawnow;
end
