bodyの慣性行列、structural nodeの姿勢など、入力ファイルの中で行列や回転行列を定義する場面は数多くあります。MBDynには、行列や回転行列を定義する色々な方法が用意されています。本項ではこれらの方法をまとめて紹介します。
matr, <a11>, <a12>, <a13>, <a21>, <a22>, <a23>, <a31>, <a32>, <a33>

sym, <a11>, <a12>, <a13>, <a22>, <a23>, <a33>

skew, <v1>, <v2>, <v3>
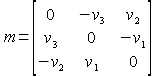
diag, <a11>, <a22>, <a33>
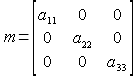
eye
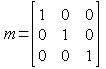
null
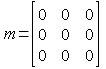
回転後の座標系のindex1の方向が(p1,p2,p3)、index2の方向が(q1,q2,q3)の時、
<index1>, <p1>, <p2>, <p3>, <index2>, <q1>, <q2>, <q3>
ここでindex1およびindex2は整数1、2、または3で、それぞれx、y、zに対応します。例えば、回転後の座標系のx方向を(0.,1.,0.)、z方向を(0.,0.,1.)へ向けたい時は次のように書きます。
1, 0., 1., 0., 3, 0., 0., 1.
2つのベクトルが正確に直行しない場合、1番目のベクトルは希望する方向を指し示し、2番目のベクトルは第3のindexの方向に垂直な平面を定めます。
特殊なケースとして、1方向だけを決めれば十分な時、例えば
1, <p1>, <p2>, <p3>, 2, guess
などとすることが可能です。guessは1番目のベクトルに垂直なベクトルを一定の方法で自動生成します。
eye
「回転なし」を表します。
matr, <a11>, <a12>, <a13>, <a21>, <a22>, <a23>, <a31>, <a32>, <a33>

直行性のチェックは行われません。
euler, <alpha>, <beta>, <gamma>
オイラー角については第7章参照。
vector, <v1>, <v2>, <v3>
ベクトルの向きが回転軸の方向を表し、ベクトルの大きさが回転角を表します。
以下はすべて、z軸周り90°の回転行列を定義します。
1, 0., 1., 0., 3, 0., 0., 1. 1, 0., 1., 0., 2, -1., 0., 0. matr, cos(pi/2.), -sin(pi/2.), 0., sin(pi/2.), cos(pi/2.), 0., 0., 0., 1. euler, 0., 0., pi/2. vector, 0., 0., pi/2.
