これまでの例題1と例題2では、剛体が唯1つだけの非常に簡単なモデルを扱いながら、MBDyn解析の基礎的な事柄について説明してきました。ここからはいよいよ、複数の剛体とジョイントを含む、より複雑なシミュレーションモデルを作成する方法について説明して行きます。まず次の例題3では、2重剛体振り子のシミュレーションモデルを作成します。このモデルでは、回転ジョイントの“revolute pin”および“revolute hinge”を使用します。
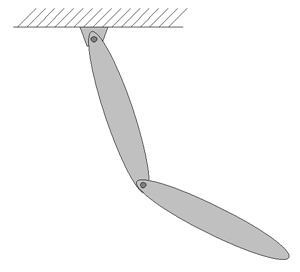
図1に示すような、2つの細長いリンクからなる2重剛体振り子を考えます。リンクの質量はともにM = 1.0 (kg)、リンクの長さはともにL = 1.0 (m)とします。1つ目のリンクが水平で、2つ目のリンクが垂直に逆立ちして静止している状態を初期条件として、そこから放たれた時の振り子の運動をMBDynでシミュレーションします。
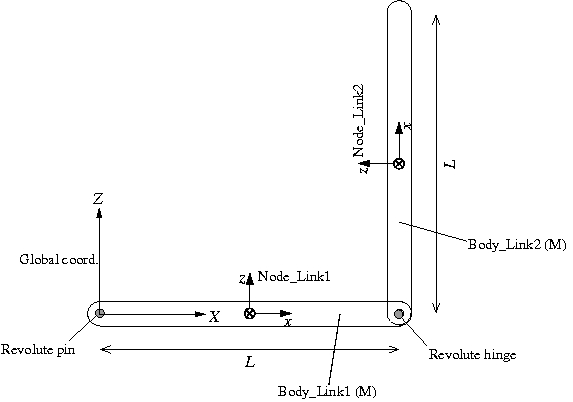
例題3のシミュレーションモデルの設計図を図2に示します。まず、1つ目のリンクと天井の接続点をグローバル座標系の原点とし、Z方向を鉛直上向きに、X軸を振り子の運動平面内に水平に取ります。各リンクのstructural node (「Node_Link1」、「Node_Link2」)は、各リンクの重心位置に長手方向をx方向とする向きで定義します。1つ目のリンクはグローバル座標系に対して“revolute pin”で接続し、リンク同士は“revolute hinge”で接続します。
このモデルで使用する2つのジョイント、“revolute hinge”と“revolute pin”について以下で説明します。
このジョイントは、2つのnodeを1軸周りの相対回転のみ許容して拘束します。revolute hingeを定義する基本的なステートメントの型は次のようになります。
joint: <label>,
revolute hinge,
<node 1>,
<relative offset 1>,
hinge, <relative orientation matrix 1>,
<node 2>,
<relative offset 2>,
hinge, <relative orientation matrix 2>;
ここで、 <relative offset 1>と<relative orientation matrix 1>、および <relative offset 2>と<relative orientation matrix 2>によって定義される2つの相対座標系の z 軸が回転軸になります。2つの相対座標系は一致させます。
このジョイントは、1つのnodeをグローバル座標系に対する1軸周りの回転のみ許容して拘束します。revolute pinを定義する基本的なステートメントの型は次のようになります。
joint: <label>,
revolute pin,
<node 1>,
<relative offset>,
hinge, <relative orientation matrix>,
<absolute pin position>,
hinge, <absolute pin orientation matrix >;
ここで、 <relative offset>と<relative orientation matrix>、および<absolute pin position>と<absolute pin orientation matrix >によって定義される2つの相対座標系の z 軸が回転軸になります。2つの相対座標系は一致させます。
リンクの太さを無視すれば、リンクの重心周りの慣性モーメントは、node座標系に対して次のようになります。
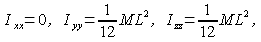
以上を踏まえて作成した、例題3の2重剛体振り子の解析を行うための入力ファイルをコード1に示します。
# double_rigid_pendulum.mbd
begin: data;
problem: initial value;
end: data;
begin: initial value;
initial time: 0.;
final time: 5.;
time step: 1.e-3;
max iterations: 10;
tolerance: 1.e-6;
end: initial value;
begin: control data;
structural nodes: 2;
rigid bodies: 2;
joints: 2;
gravity;
end: control data;
# Design Variables
set: real M = 1.; # Mass of Link1 and Link2
set: real L = 1.; # Length of Link1 and Link2
# Node Labels
set: integer Node_Link1 = 1;
set: integer Node_Link2 = 2;
# Body Labels
set: integer Body_Link1 = 1;
set: integer Body_Link2 = 2;
# Joint Labels
set: integer JoRevp_Link1 = 1;
set: integer JoRevh_Link1_Link2 = 2;
begin: nodes;
structural: Node_Link1, dynamic,
1./2.*L, 0., 0., # absolute position
eye, # absolute orientation
null, # absolute velocity
null; # absolute angular velocity
structural: Node_Link2, dynamic,
L, 0., 1./2.*L, # absolute position
euler, 0., -pi/2., 0., # absolute orientation
null, # absolute velocity
null; # absolute angular velocity
end: nodes;
begin: elements;
body: Body_Link1, Node_Link1,
M, # mass
null, # relative center of mass
diag, 0., M*L^2./12., M*L^2./12.; # inertia matrix
body: Body_Link2, Node_Link2,
M, # mass
null, # relative center of mass
diag, 0., M*L^2./12., M*L^2./12.; # inertia matrix
joint: JoRevp_Link1,
revolute pin,
Node_Link1,
-1./2.*L, 0., 0., # relative offset
hinge, 1, 1., 0., 0., 3, 0., 1., 0., # relative axis orientation
null, # absolute pin position
hinge, 1, 1., 0., 0., 3, 0., 1., 0.; # absolute pin orientation
joint: JoRevh_Link1_Link2,
revolute hinge,
Node_Link1,
1./2.*L, 0., 0., # relative offset
hinge, 1, 1., 0., 0., 3, 0., 1., 0., # relative axis orientation
Node_Link2,
-1./2.*L, 0., 0., # relative offset
hinge, 1, 1., 0., 0., 3, 0., 1., 0.; # relative axis orientation
gravity: 0., 0., -1., const, 9.81;
end: elements;
シミュレーション結果のアニメーションを動画1に示します。
