前項で作成した2重剛体振り子のシミュレーションモデルは、一定の初期位置からのシミュレーションしか行えないため、汎用性に欠けます。そこで、様々な初期位置からのシミュレーションが行えるようにモデルを改良してみましょう。ここでは、複雑なモデルを構築する上で大変便利な、参照座標系“reference”を活用します。
前項の例題3と同様に、2つの細長いリンクからなる2重剛体振り子を考えます。リンク1が鉛直線となす角をθ1、リンク2がリンク1となす角をθ2とする時、初期のθ1とθ2を任意に変えてシミュレーションを行えるようなシミュレーションモデルの入力ファイルを作成します。
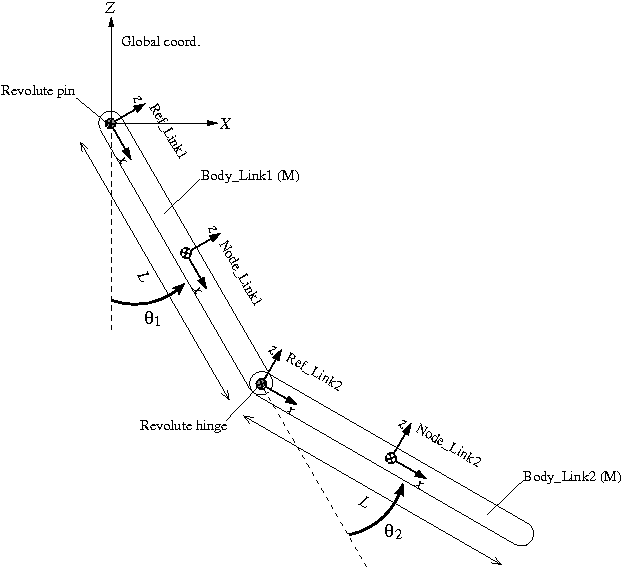
例題4のシミュレーションモデルの設計図を図1に示します。初期のθ1とθ2を変数として、一般的な配置でモデルを作成します。各リンクのstructural node(「Node_Link1」、「Node_Link2」)は、各リンクの重心位置に長手方向をx方向とする向きで定義します。リンク1はグローバル座標系に対してrevolute pinで接続し、リンク1とリンク2はrevolute hingeで接続します。図のように2つの“reference”「Ref_Link1」と「Ref_Link2」を定義することで、モデル構築が比較的容易になります。
referenceはモデルを構築する際に便宜的に定義することができる参照座標系です。referenceを定義するステートメントの型は次のようになります。
reference: <label> ,
<absolute position> ,
<absolute orientation matrix> ,
<absolute velocity> ,
<absolute angular velocity> ;
referenceの定義は入力ファイルのどこでも(ブロック外でも)行うことができます。このように定義したreferenceは、nodeやジョイントを定義するステートメントの中で次の量を入力する際に参照することができます。
これらの量(value)を既存のreferenceを参照して入力する場合には、キーワード「reference」を用いて次のように記述します。
reference, <reference label>, <value>
referenceを利用して、本例題の2つのリンクのnodeを定義する手順を以下に示します。
まず、reference「Ref_Link1」を次のように定義します。(「Ref_Link1」はグローバル座標系をy軸周りにπ/2-θ1だけ回転して得られる座標系です。)
set: integer Ref_Link1 = 1;
reference: Ref_Link1,
null, # absolute position
euler, 0., pi/2.-theta1, 0., # absolute orientation
null, # absolute velocity
null; # absolute angular velocity
reference「Ref_Link1」を参照して、node「Node_Link1」を次のように定義することができます。(「Node_Link1」は「Ref_Link1」をそのx方向にL/2だけ平行移動して得られます。)
set: integer Node_Link1 = 1;
structural: Node_Link1, dynamic,
reference, Ref_Link1, 1./2.*L, 0., 0., # absolute position
reference, Ref_Link1, eye, # absolute orientation
reference, Ref_Link1, null, # absolute velocity
reference, Ref_Link1, null; # absolute angular velocity
既存のreferenceを参照して別のreferenceを定義することも可能です。ここでは、reference「Ref_Link1」を参照して、reference「Ref_Link2」を定義します。(「Ref_Link2」は「Ref_Link1」をそのx方向にLだけ平行移動し、さらにそのy軸周りに-θ2だけ回転して得られます。)
set: integer Ref_Link2 = 2;
reference: Ref_Link2,
reference, Ref_Link1, L, 0., 0., # absolute position
reference, Ref_Link1, euler, 0., -theta2, 0., # absolute orientation
reference, Ref_Link1, null, # absolute velocity
reference, Ref_Link1, null; # absolute angular velocity
最後に、reference「Ref_Link2」を参照して、node「Node_Link2」を定義します。(「Node_Link2」は「Ref_Link2」をそのx方向にL/2だけ平行移動して得られます。)
set: integer Node_Link2 = 2;
structural: Node_Link2, dynamic,
reference, Ref_Link2, 1./2.*L, 0., 0., # absolute position
reference, Ref_Link2, eye, # absolute orientation
reference, Ref_Link2, null, # absolute velocity
reference, Ref_Link2, null; # absolute angular velocity
ちなみに、referenceを用いずにnode「Node_Link2」を定義するとどのようになるでしょうか?node「Node_Link2」の絶対位置は、
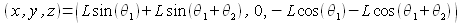
ですから、次のように定義できます。しかし、記述がかなり煩雑になってしまうことが分かります。
set: integer Node_Link2 = 2;
structural: Node_Link2, dynamic,
L*sin(theta1)+L*sin(theta1+theta2), 0., -L*cos(theta1)-L*cos(theta1+theta2), # absolute position
euler, 0., pi-(theta1+theta2), 0., # absolute orientation
null, # absolute velocity
null; # absolute angular velocity
以上を踏まえて作成した、例題4の2重剛体振り子の解析を行うための入力ファイルをコード1に示します。
# double_rigid_pendulum_2.mbd
begin: data;
problem: initial value;
end: data;
begin: initial value;
initial time: 0.;
final time: 5.;
time step: 1.e-3;
max iterations: 10;
tolerance: 1.e-6;
end: initial value;
begin: control data;
structural nodes: 2;
rigid bodies: 2;
joints: 2;
gravity;
end: control data;
# Design Variables
set: real M = 1.; # Mass of Link1 and Link2
set: real L = 1.; # Length of Link1 and Link2
set: real theta1 = pi/6.; # Initial angle of Link1 w.r.t vertical line
set: real theta2 = pi/6.; # Initial angle of Link2 w.r.t Link1
# Reference Labels
set: integer Ref_Link1 = 1;
set: integer Ref_Link2 = 2;
# Node Labels
set: integer Node_Link1 = 1;
set: integer Node_Link2 = 2;
# Body Labels
set: integer Body_Link1 = 1;
set: integer Body_Link2 = 2;
# Joint Labels
set: integer JoRevp_Link1 = 1;
set: integer JoRevh_Link1_Link2 = 2;
# Reference
reference: Ref_Link1,
null, # absolute position
euler, 0., pi/2.-theta1, 0., # absolute orientation
null, # absolute velocity
null; # absolute angular velocity
reference: Ref_Link2,
reference, Ref_Link1, L, 0., 0., # absolute position
reference, Ref_Link1, euler, 0., -theta2, 0., # absolute orientation
reference, Ref_Link1, null, # absolute velocity
reference, Ref_Link1, null; # absolute angular velocity
begin: nodes;
structural: Node_Link1, dynamic,
reference, Ref_Link1, 1./2.*L, 0., 0., # absolute position
reference, Ref_Link1, eye, # absolute orientation
reference, Ref_Link1, null, # absolute velocity
reference, Ref_Link1, null; # absolute angular velocity
structural: Node_Link2, dynamic,
reference, Ref_Link2, 1./2.*L, 0., 0., # absolute position
reference, Ref_Link2, eye, # absolute orientation
reference, Ref_Link2, null, # absolute velocity
reference, Ref_Link2, null; # absolute angular velocity
end: nodes;
begin: elements;
body: Body_Link1, Node_Link1,
M, # mass
null, # relative center of mass
diag, 0., M*L^2./12., M*L^2./12.; # inertia matrix
body: Body_Link2, Node_Link2,
M, # mass
null, # relative center of mass
diag, 0., M*L^2./12., M*L^2./12.; # inertia matrix
joint: JoRevp_Link1,
revolute pin,
Node_Link1,
reference, Ref_Link1, null, # relative offset
hinge, reference, Ref_Link1, 1, 1., 0., 0., 3, 0., 1., 0., # relative axis orientation
reference, Ref_Link1, null, # absolute pin position
hinge, reference, Ref_Link1, 1, 1., 0., 0., 3, 0., 1., 0.; # absolute pin orientation
joint: JoRevh_Link1_Link2,
revolute hinge,
Node_Link1,
reference, Ref_Link2, null, # relative offset
hinge, reference, Ref_Link2, 1, 1., 0., 0., 3, 0., 1., 0., # relative axis orientation
Node_Link2,
reference, Ref_Link2, null, # relative offset
hinge, reference, Ref_Link2, 1, 1., 0., 0., 3, 0., 1., 0.; # relative axis orientation
gravity: 0., 0., -1., const, 9.81;
end: elements;
θ1とθ2の初期値をどちらもπ/6とした時のシミュレーション結果のアニメーションを動画1に示します。
