ジョイントを含んだモデルでMBDyn解析を行った場合には、拡張子が「jnt」の出力ファイル(以後、jntファイル)が生成されます。jntファイルには、ジョイント反力やジョイント特有のデータが書き出されます。本項では、前項の例題4の解析で出力されるjntファイルを用いて、ジョイント出力の扱い方を説明します。
例題4の解析で出力されるjntファイル「double_rigid_pendulum_2.jnt」の内容を表計算ソフトウェアで表示した様子を図1に示します。
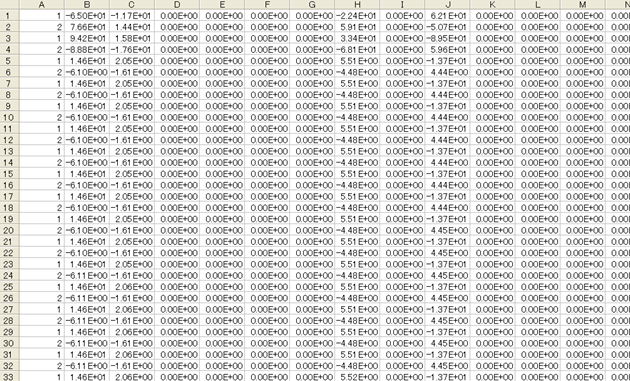
一般にjntファイルのデータは、全てのジョイントに共通の標準部と、ジョイントの種類によって異なる非標準部に分けられます。標準部は1〜13列目で次のような構成になっています。
図1のデータを見ると、ジョイント「1」のデータとジョイント「2」のデータが一行ごとに交互に書き出されているのが分かります。このようにジョイントが2つ存在する場合には、各時間ステップでそれぞれのジョイントのデータが1行ずつ書き出されます。一般にN個のジョイントがある場合には、各時間ステップでN個のジョイントに対応するN行のデータが書き出されます。
このように、jntファイルの形式は第11項で説明したmovファイルの形式と同じです。従って、jntファイルのデータを処理する場合にも、第11項で紹介したMATLAB関数「MBDynLoad」が使用できます。
例題4の解析で出力されるjntファイル「double_rigid_pendulum_2.jnt」をMATLABに読み込んで、revolute pinにかかるジョイント反力の時間変化をプロットしてみましょう。
まず、関数「MBDynLoad」を用いて「double_rigid_pendulum_2.jnt」のデータを読み込みます。
[LABEL,DATA] = MBDynLoad('double_rigid_pendulum_2.jnt');
次に、revolute pinのラベルが「1」であることを考慮して、revolute pinにかかるジョイント反力の各成分の時系列データベクトルを次のように作成します。
f1x = DATA(:,2,LABEL==1); f1y = DATA(:,3,LABEL==1); f1z = DATA(:,4,LABEL==1); F1x = DATA(:,8,LABEL==1); F1y = DATA(:,9,LABEL==1); F1z = DATA(:,10,LABEL==1);
ここで、(f1x, f1y, f1z) はローカル座標系における3成分、(F1x, F1y, F1z) はグローバル座標系における3成分です。revolute pinのローカル座標系とは、revolute pinを定義するステートメント内の“hinge”で定義され、リンク1に固定された座標系を指します。
一方、時間データベクトルは次のように作成できます。
t = 1.e-3*[0:length(f1x)-1]';
これらの時系列データベクトルを用いれば、revolute pinにかかるジョイント反力の各成分の時間変化のグラフを、例えば次のようにプロットできます。このグラフを図2に示します。
figure(1) subplot(2,1,1) plot(t,f1x,t,f1y,'-.',t,f1z,'--') subplot(2,1,2) plot(t,F1x,t,F1y,'-.',t,F1z,'--')
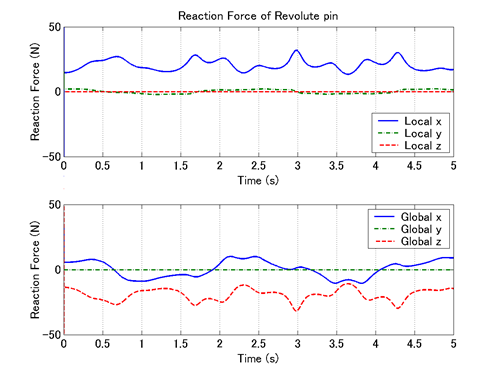
次に、revolute pinにかかるジョイント反力の大きさを調べて見ましょう。力の大きさは、成分の二乗和の平方根として求められますので、次のようにしてジョイント反力の大きさの時系列データベクトルを作成できます。
f1 = sqrt(f1x.^2+f1y.^2+f1z.^2);
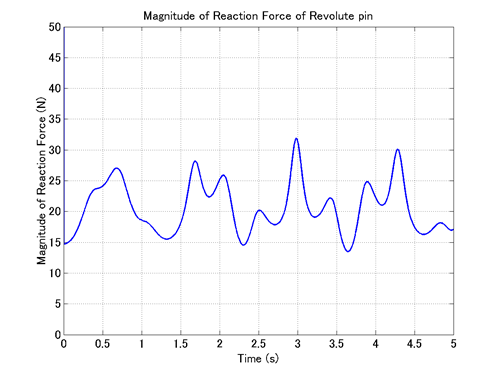
その後、次のように入力すれば、revolute pinにかかるジョイント反力の大きさの時間変化のグラフをプロットできます。このグラフを図3に示します。
figure(2) plot(t,f1)
尚、上ではローカル座標系の3成分を用いて力の大きさを求めていますが、力の大きさは座標系に拠らないので、グローバル座標系の3成分を用いても同じ結果が得られます。
jntファイルには1〜13列目の標準データに加え、ジョイントの種類によっては非標準のデータが出力される場合があります。revolute pin/hingeの場合には、次の非標準データが出力されます。
では、このデータを利用して、例題4の解析結果からθ1とθ2の時間変化をプロットしてみましょう。これは、次のコード1に示すMATLABスクリプトによって行えます(ただし、θ1とθ2の初期値がどちらもπ/6(= 30 deg)の場合)。このスクリプトによって描画されるグラフを図4に示します。
% plot_theta.m
clear; close all;
[LABEL,DATA] = MBDynLoad('double_rigid_pendulum_2.jnt');
a1z = DATA(:,16,LABEL==1);
a2z = DATA(:,16,LABEL==2);
t = 1.e-3*[0:length(a1z)-1]';
theta1 = 30-a1z;
theta2 = 30-a2z;
plot(t,theta1,t,theta2,'LineWidth',1.5)
grid on;
set(gca,'FontSize',14);
xlabel('Time','FontSize',14);
ylabel('Angle (deg)','FontSize',14);
title('Joint Angles');
legend('\theta_1','\theta_2',0);