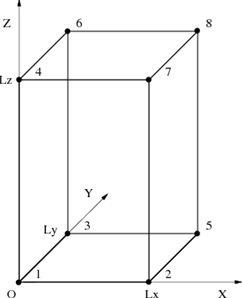
plot3d コマンドを用いて、6個の面を組み合わせて直方体を作成してみましょう。まずは図1に示すように、頂点の1つが座標系の原点と一致し、各辺が座標軸と平行な場合を考えてみます(これを基本配置と呼ぶことにします)。この場合、3辺の長さ(Lx, Ly, Lz)から、8個の頂点の座標は明らかです。6個の面は次の6通りの頂点の結合で与えられます。
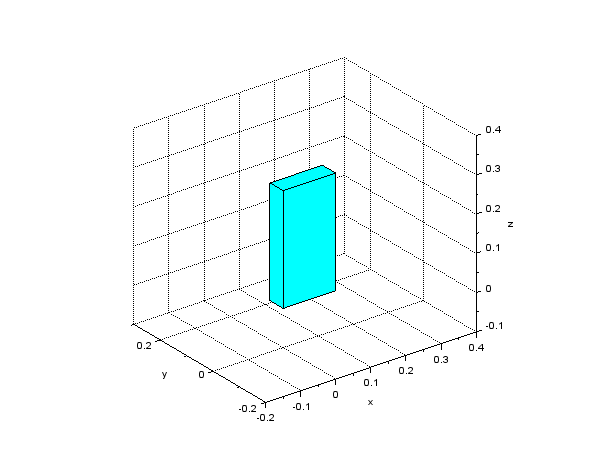
基本配置の直方体を作成するScilabスクリプトをコード1に、このスクリプトによる描画の結果を図2にそれぞれ示します。スクリプト中の genpat() は、形状の頂点と面の行列データから plot3d に入力するパッチデータを作成する関数で、コード2のように定義されます。
// make_block_special.sce
clear; xdel(winsid());
exec('genpat.sci', -1);
// Side lengths
Lx = 0.15;
Ly = 0.05;
Lz = 0.30;
// Vertices
vertices = [
0, 0, 0; // #1
Lx, 0, 0; // #2
0, Ly, 0; // #3
0, 0, Lz; // #4
Lx, Ly, 0; // #5
0, Ly, Lz; // #6
Lx, 0, Lz; // #7
Lx, Ly, Lz]; // #8
// Faces
faces = [
1, 2, 5, 3; // #1
1, 3, 6, 4; // #2
1, 4, 7, 2; // #3
4, 7, 8, 6; // #4
2, 5, 8, 7; // #5
3, 6, 8, 5]; // #6
// Patches
patches = genpat(vertices, faces);
// Draw patches
h_fig = figure;
h_fig.background = 8;
h_pat = plot3d(patches.x, patches.y, patches.z);
h_pat.color_mode = 4;
h_pat.foreground = 1;
h_pat.hiddencolor = 4;
// Axes settings
xlabel("x"); ylabel("y"); zlabel("z");
h_axes = gca();
h_axes.isoview = "on";
h_axes.box = "off";
h_axes.rotation_angles = [63.5, -127];
h_axes.data_bounds = [-0.2, -0.2, -0.1; 0.4, 0.3, 0.4];
xgrid;
function patches = genpat(vertices, faces)
// Generate patches data from vertices and faces
patches.x = vertices(:,1)(faces');
patches.y = vertices(:,2)(faces');
patches.z = vertices(:,3)(faces');
endfunction