前回の記事では、独楽(こま)のシミュレーションを行ってみました。
せっかくシミュレーションプログラムを作ったので、少しこれを使って、独楽の運動について考えてみましょう。
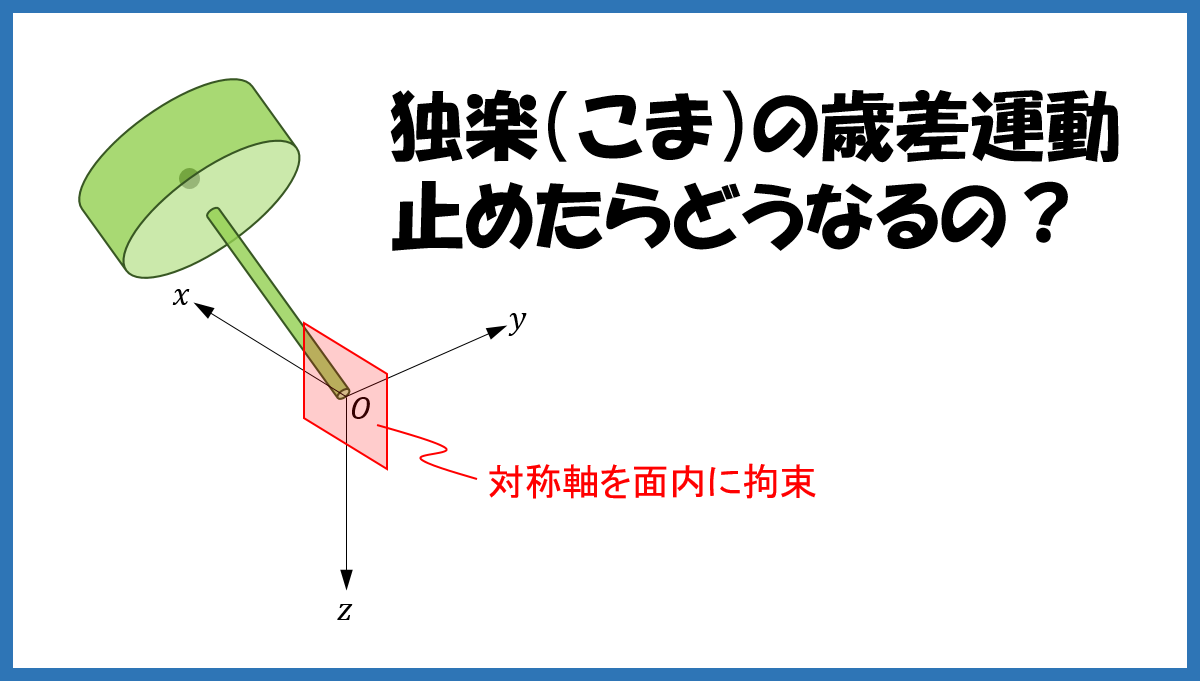
なぜ独楽は倒れないの?
前回の記事のシミュレーション結果でも見られたように、独楽は歳差運動(回転軸が円錐を描くように振れ回る運動)をしながら、重力に逆らって立っている状態を保ちます。
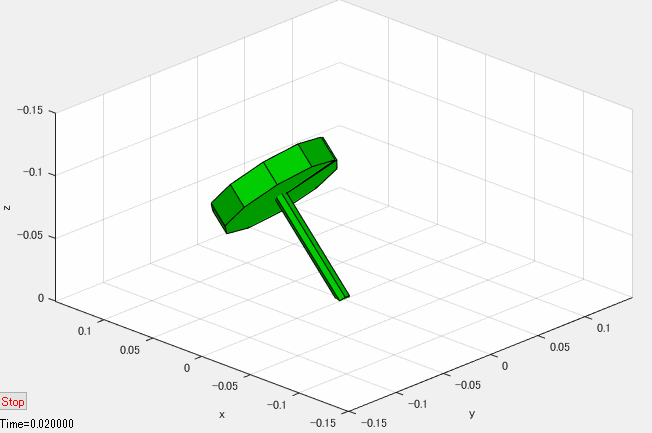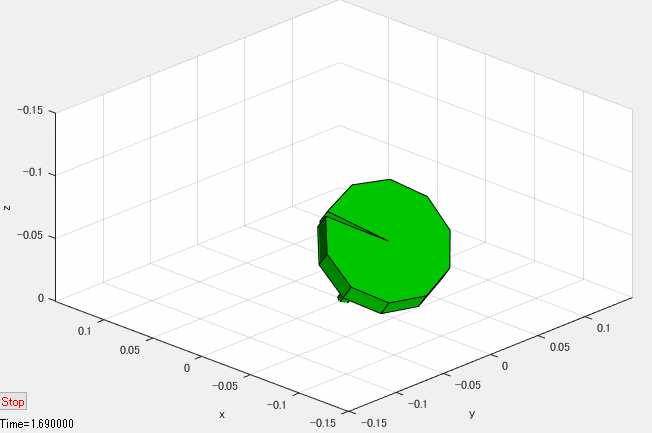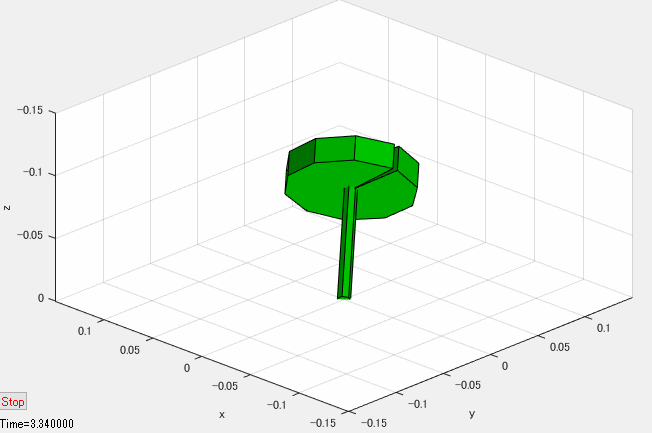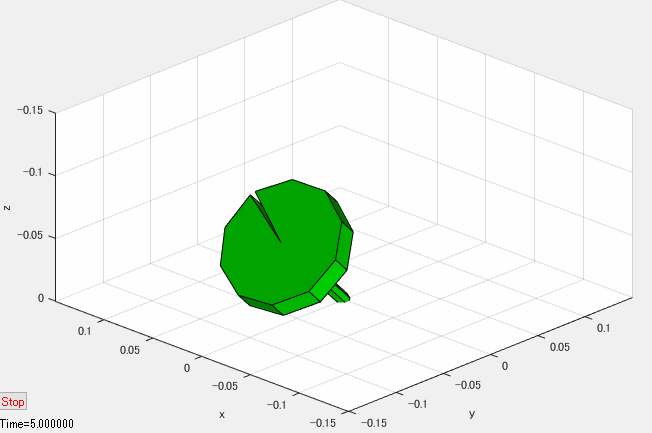
独楽のシミュレーション結果のアニメーション
なぜ独楽は倒れないのでしょうか?歳差運動に秘密があるのでしょうか?
もし歳差運動を止めたら、つまり、歳差運動できないように独楽を拘束したらどうなるのでしょうか?その場合は倒れてしまうのでしょうか?シミュレーションで試してみましょう。
対称軸の方位角を拘束
下図において、点 \(O\) は独楽の支点、\(O-xyz\) は慣性系に固定された座標系、\(O-x^{\prime}y^{\prime}z^{\prime}\) は独楽に固定された座標系、\(\left(\psi, \theta, \phi\right)\) は \(O-xyz\) に対する \(O-x^{\prime}y^{\prime}z^{\prime}\) のオイラー角です。
独楽が歳差運動できないように拘束するには、対称軸の方位角 \(\psi\) を固定します。
$$ \psi \equiv 0 \tag{1}$$
今回のシミュレーションモデルで、この拘束を簡単に実現するために、次のような \(z\) 軸周りの回転ばねモーメントを導入します。
$$
\mathbf{M}_c =
\begin{bmatrix}
0 \\ 0 \\ -k_\psi \psi
\end{bmatrix} \tag{2}
$$
ここで、\(k_\psi\) はばね定数です。ばね定数 \(k_\psi\) を十分大きな値に設定すれば、\(\psi\approx 0\) になり、式(1)の拘束が近似的に実現します。
式(2)のモーメントの座標系 \(O-x^{\prime}y^{\prime}z^{\prime}\) による成分表示は、回転行列 \(\mathbf{R}\) を用いて次のように求められます。
$$ \mathbf{M}_c^\prime = \mathbf{R}^T \mathbf{M}_c \tag{3} $$
さらに、重力のモーメントを \(\mathbf{M}_g^\prime\) とすれば、独楽に働く重力と拘束力の合モーメントは
$$ \mathbf{M}^\prime = \mathbf{M}_g^\prime + \mathbf{M}_c^\prime \tag{4} $$
となります。この合モーメントを前回の記事で作成したシミュレーションプログラムに適用して、シミュレーションを行ってみます。
Scilab用シミュレーションプログラム
回転軸の方位角を拘束した独楽の、Scilab用シミュレーションプログラムを以下に示します。前回の記事のプログラムを一部改修したものです。
次の常微分方程式関数の定義スクリプトでは、式(2)(3)(4)に従って、方位角拘束モーメントを追加しています。元のスクリプトと区別するために関数名とファイル名も変更しました。
// top_constrained.sci
/******************************************************************************
* 独楽(こま)の常微分方程式関数(方位角拘束)の定義
******************************************************************************/
// 独楽の常微分方程式関数
function [x_dot, request] = top_constrained(t, x)
// パラメータ
m = 1; // [kg] 質量
Ia = 0.02; // [kg*m^2] 回転軸周りの慣性モーメント
It = 0.01; // [kg*m^2] 重心を通り回転軸に直角な軸周りの慣性モーメント
l = 0.1; // [m] 重心と支点の距離
g = 9.8; // [m/s^2] 重力加速度
// 重心位置(剛体枠参照)
rG = [l; 0; 0];
// 支点周りの慣性行列(剛体枠参照)
I = diag([Ia, It, It]) - m*tilde(rG)*tilde(rG);
// オイラー角
psi = x(1); // [rad] 方位角
theta = x(2); // [rad] 傾角
phi = x(3); // [rad] 回転角
// 角速度ベクトル(剛体枠参照)
w = [x(4); x(5); x(6)];
// 三角関数値
S_psi = sin(psi);
S_theta = sin(theta);
S_phi = sin(phi);
C_psi = cos(psi);
C_theta = cos(theta);
C_phi = cos(phi);
// 回転行列
R = [
C_psi*C_theta, C_psi*S_theta*S_phi - C_phi*S_psi, S_psi*S_phi + C_psi*C_phi*S_theta;
C_theta*S_psi, C_psi*C_phi + S_psi*S_theta*S_phi, C_phi*S_psi*S_theta - C_psi*S_phi;
-S_theta, C_theta*S_phi, C_theta*C_phi];
// 重力モーメント(剛体枠参照)
Mg = tilde(rG)*R'*[0; 0; m*g];
// 方位角拘束モーメント(剛体枠参照)
k_psi = 1e5; // [Nm/rad]
Mc = R'*[0; 0; -k_psi*psi];
// 合モーメント(剛体枠参照)
M = Mg + Mc;
// 角速度ベクトルの時間微分(オイラーの運動方程式、剛体枠参照)
w_dot = I\(M - tilde(w)*I*w);
// オイラー角の時間微分
a_dot = [
0, S_phi/C_theta, C_phi/C_theta;
0, C_phi, -S_phi;
1, S_phi*S_theta/C_theta, C_phi*S_theta/C_theta]*w;
// 状態ベクトルの時間微分
x_dot = [a_dot; w_dot];
// リクエスト変数
if argn(1) > 1
request.rG_inr = R*rG; // 重心の位置ベクトル(慣性枠参照)
end
endfunction
// チルダオペレータ
function a_tilde = tilde(a)
a_tilde = [
0, -a(3), a(2);
a(3), 0, -a(1);
-a(2), a(1), 0];
endfunction
次のシミュレーション実行スクリプトでは、「exec」で読み込む関数ファイル名とodeソルバーに渡す関数名を変更し、重心の軌跡プロットの「data_bounds」を調整しています。
また、後で説明する理由から、シミュレーション終了時間を0.3秒と短くしています。
// simulate_top_constrained.sce
/******************************************************************************
* 独楽(こま)の動力学シミュレーション(方位角拘束)を実行する
******************************************************************************/
clear; // ワークスペース変数をクリア
for i=winsid(), close(scf(i)), end; // 全ての図を閉じる
exec('top_constrained.sci'); // 独楽の常微分方程式関数(方位角拘束)を読み込み
// 初期条件の設定
psi_0 = 0; // [rad] 方位角
theta_0 = %pi/4; // [rad] 傾角
phi_0 = 0; // [rad] 回転角
wx_0 = 10*%pi; // [rad/s] x'軸周り角速度
wy_0 = 0; // [rad/s] y'軸周り角速度
wz_0 = 0; // [rad/s] z'軸周り角速度
x0 = [psi_0; theta_0; phi_0; wx_0; wy_0; wz_0]; // 状態ベクトルの初期値
// シミュレーション時間の設定
t0 = 0; // [s] 開始
tf = 0.3; // [s] 終了
dt = 0.001; // [s] 出力サンプル時間
t = t0:dt:tf; // [s] 出力時間ベクトル
// 常微分方程式ソルバーの実行
x = ode(x0, t0, t, top_constrained); // top_constrainedは独楽の常微分方程式関数
// シミュレーション結果
nt = length(t); // 出力データ点数
psi = x(1,:); // [rad] 方位角
theta = x(2,:); // [rad] 傾角
phi = x(3,:); // [rad] 回転角
wx = x(4,:); // [rad/s] x'軸周り角速度
wy = x(5,:); // [rad/s] y'軸周り角速度
wz = x(6,:); // [rad/s] z'軸周り角速度
// リクエスト変数の初期化
rG_inr = zeros(3,nt); // 重心の位置ベクトル(慣性座標系参照)
// リクエスト変数の評価
for i = 1:nt
[x_dot, request] = top_constrained(t(i), x(:,i));
rG_inr(:,i) = request.rG_inr; // [m] 重心の位置ベクトル(慣性座標系参照)
end
// プロット設定
thickness = 2;
font_size = 3;
// オイラー角の時系列プロット
figure('figure_size', [626,700], 'background', -2);
margin_left = 0.16;
subplot(3,1,1);
plot(t, psi*180/%pi, 'thickness', thickness);
margins = gca().margins;
margins(1) = margin_left;
set(gca(), 'font_size', font_size, 'margins', margins);
ylabel('$\text{方位角}\\ \psi \text{ [deg]}$', 'font_size', font_size);
xgrid;
subplot(3,1,2);
plot(t, theta*180/%pi, 'thickness', thickness);
margins = gca().margins;
margins(1) = margin_left;
set(gca(), 'font_size', font_size, 'margins', margins);
ylabel('$\text{傾角}\\ \theta \text{ [deg]}$', 'font_size', font_size);
xgrid;
subplot(3,1,3);
plot(t, phi*180/%pi, 'thickness', thickness);
margins = gca().margins;
margins(1) = margin_left;
set(gca(), 'font_size', font_size, 'margins', margins);
ylabel('$\text{回転角}\\ \phi \text{ [deg]}$', 'font_size', font_size);
xgrid;
// 重心の軌跡プロット
figure('background', -2);
param3d(rG_inr(1,:), rG_inr(2,:), rG_inr(3,:));
set(gce(), 'thickness', thickness, 'foreground', 2);
title('重心の軌跡');
data_bounds = [-0.1, -0.1, -0.1; 0.1, 0.1, 0.1];
set(gca(), 'data_bounds', data_bounds, 'axes_reverse', ["off","on","on"],..
'rotation_angles', [72.5,131.5], 'font_size', font_size);
xgrid;
シミュレーション結果
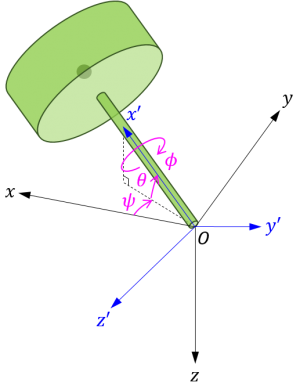
上記のプログラムを実行して得られたシミュレーション結果のプロットを以下に示します。
- オイラー角の時系列プロット
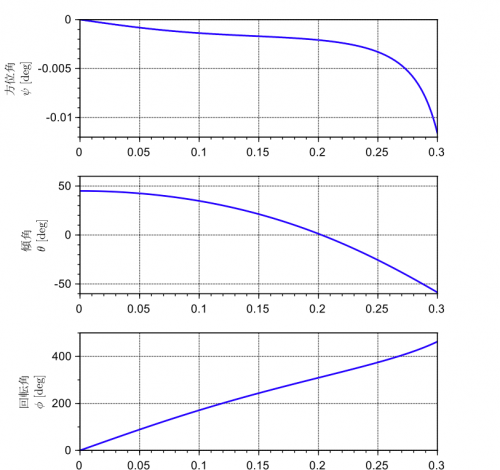
- 重心の軌跡プロット
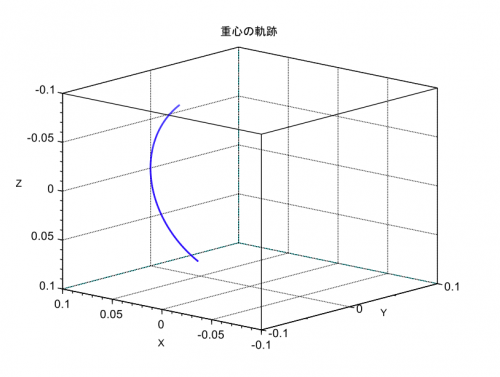
下図はシミュレーション結果のアニメーションです。(かなりスローで再生しています。)
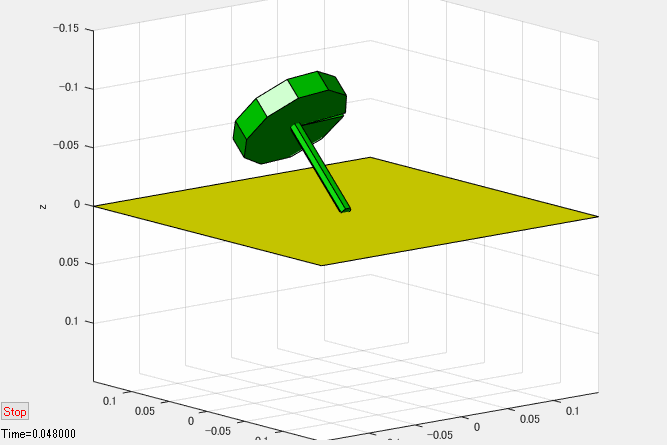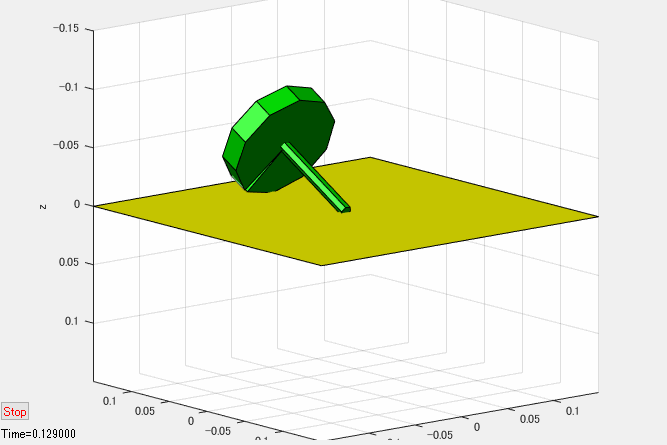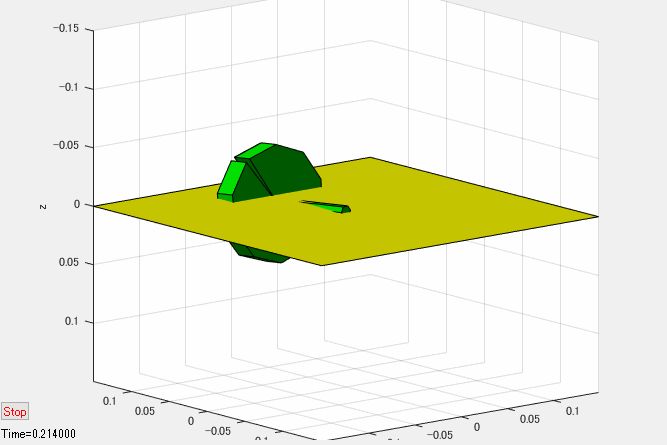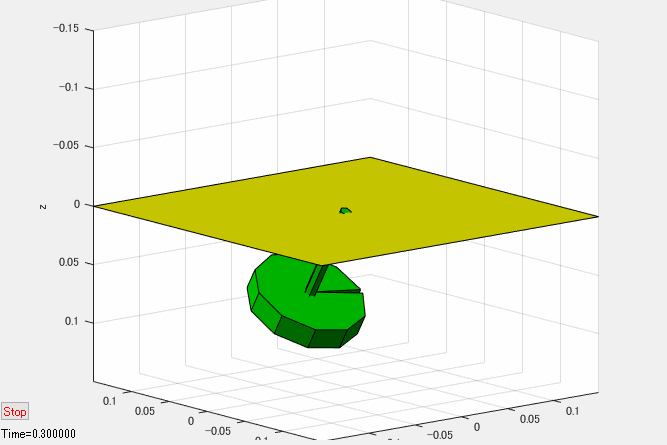
シミュレーション結果が示すように、歳差運動できないように独楽を拘束すると、独楽は重力に全く逆らえず、倒れてしまいます。この結果から、独楽が倒れないためには歳差運動が必要であることが分かります。
ところで、このシミュレーションでは独楽が倒れてしまうので、シミュレーションを継続するとある時点で独楽は傾角が \(\theta = -\pi\)[rad] の点(独楽が真下を向く状態)を通過します。しかし、このプログラムで使用している z-y-x型のオイラー角は \(\theta=\pm\pi\)[rad] で特異姿勢となるため、特異姿勢に至る前の時刻0.3秒でシミュレーションを終了しています。
まとめ
この記事では、独楽のシミュレーションプログラムを一部改修し、歳差運動できないように拘束した独楽の運動をシミュレーションしてみました。シミュレーション結果から、歳差運動できないように拘束した独楽は倒れてしまうこと、つまり、独楽が倒れないためには歳差運動が必要であることが分かりました。
では、なぜ歳差運動が起こり、そしてなぜ歳差運動によって独楽は倒れなくなるのでしょうか。その理由は、ジャイロモーメント呼ばれる見かけのモーメントで説明することができます。ジャイロモーメントと独楽が倒れない理由については、次の記事で解説します。
最後まで読んでいただきありがとうございました。この記事がご参考になれば幸いです。



コメント