独楽(こま)の動きって不思議ですよね。回っている独楽はなぜ倒れないのでしょうか?
独楽が倒れない理由は、ジャイロモーメントと呼ばれる見かけのモーメントによって説明することができます。この記事では、ジャイロモーメントとは何か、そして独楽が倒れない理由について詳しく解説します。
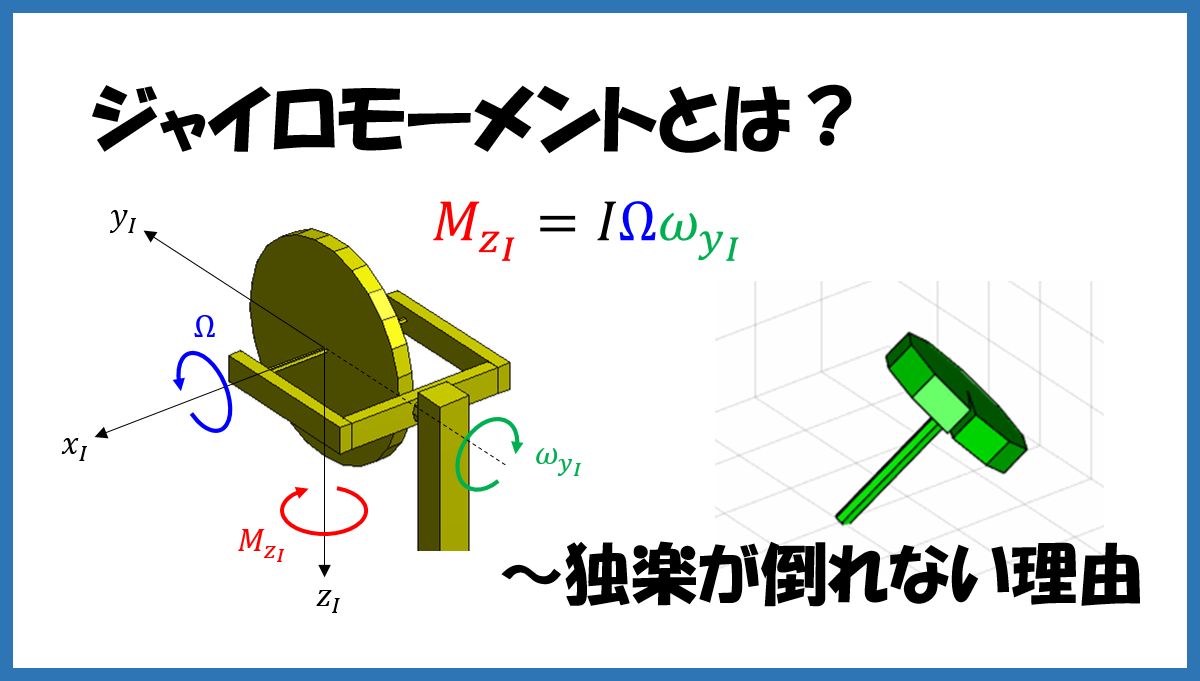
ジャイロモーメントとは?
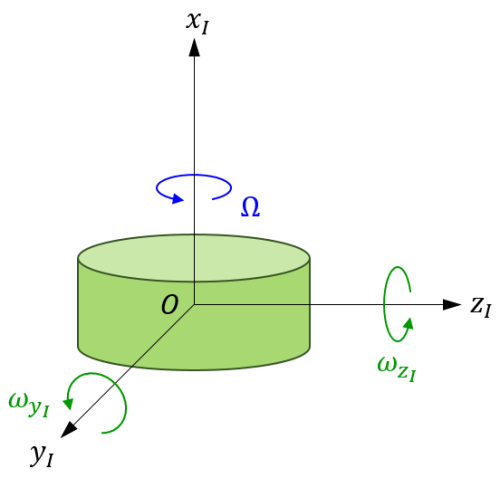
下図のように、軸対称な剛体が対称軸上の固定点または重心の点 \(O\) を中心として回転運動しているとします。
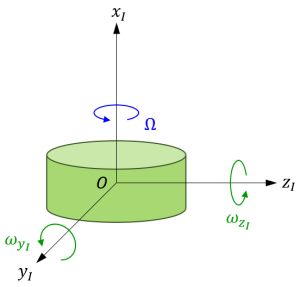
剛体の対称軸を \(x_I\) 軸とし、自身が \(x_I\) 軸周りに角速度を持たないような座標系 \(O-x_I y_I z_I\) を考えます。座標系 \(O-x_I y_I z_I\) は、\(y_I\) 軸周りと \(z_I\) 軸周りには剛体と連動して回転しますが、\(x_I\) 軸周りには回転しない中間的な座標系です。剛体は座標系 \(O-x_I y_I z_I\) に対し、 \(x_I\) 軸周りに回転します。
剛体の対称軸(\(x_I\) 軸)周りの慣性モーメントを \(I_a\)、 \(x_I, y_I, z_I\) 軸周りの角速度をそれぞれ \(\Omega, \omega_{y_I}, \omega_{z_I}\) とすると、座標系 \(O-x_I y_I z_I\) において、以下の式で表される見かけのモーメントが発生します。
$$\mathbf{M}_\text{gyro}^{(I)}=\begin{bmatrix}
0 \\ -I_a\Omega\omega_{z_I} \\ I_a\Omega\omega_{y_I} \\
\end{bmatrix} \tag{1}$$
この見かけのモーメントをジャイロモーメント(gyroscopic moment)と呼びます。(式(1)の導出については後の項で解説します。)
式(1)によれば、\(\Omega\neq 0\) の時、\(y_I\) 軸周りの角速度 \(\omega_{y_I}\) によって \(z_I\) 軸周りのモーメント \(I_a\Omega\omega_{y_I}\)が発生し、\(z_I\) 軸周りの角速度 \(\omega_{z_I}\) によって \(y_I\) 軸周りのモーメント \(-I_a\Omega\omega_{z_I}\) が発生します。(下図)
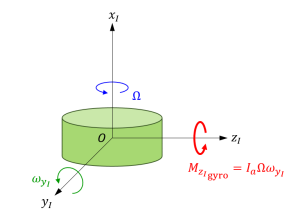
\(y_I\) 軸周りの角速度に起因する \(z_I\) 軸周りのジャイロモーメント
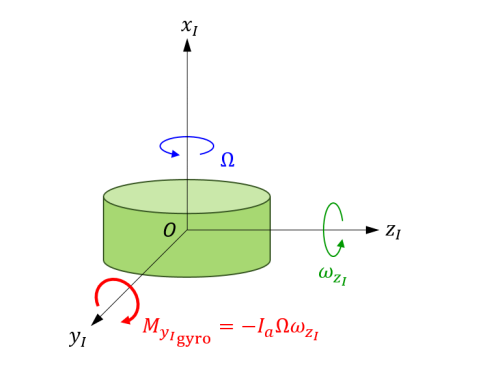
\(z_I\) 軸周りの角速度に起因する \(y_I\) 軸周りのジャイロモーメント
一般に、ある軸周りに自転運動する剛体において、自転軸の角度を変える方向に付加角速度が生じた時、自転軸と付加角速度の両方に垂直な軸周りに見かけのモーメントが発生し、これをジャイロモーメントと呼びます。特に、軸対称剛体の場合には、ジャイロモーメントは式(1)で与えられます。
ジャイロモーメント実験機械モデル
例として、下図のような機械モデルを考えてみましょう。
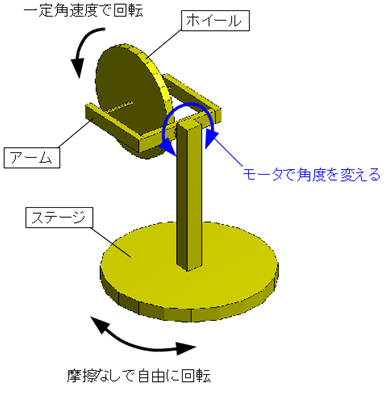
この機械モデルは、ステージ、アーム、ホイールの3つの可動部分からなります。ステージは垂直な軸の回転ジョイントで地面に接続され、地面に対して摩擦なしで回転することができます。アームは水平な軸の回転ジョイントでステージに固定された支柱に接続され、モータで支柱に対する角度を変えることができます。ホイールは回転ジョイントでアームに接続され、アームに対して一定の角速度で回転します。ホイールの回転軸とアームの回転軸は直交するとします。
さて、下図のように、ホイールの回転軸を \(x_I\) 軸、アームの回転軸を \(y_I\) 軸とする座標系 \(O-x_{I}y_{I}z_{I}\) はアームに固定されます。
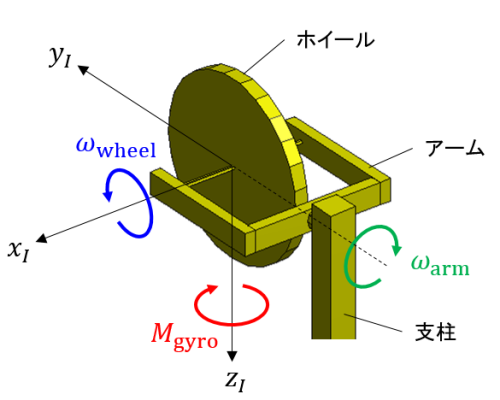
ホイールの \(x_I\) 軸周りの慣性モーメントを \(I_\text{wheel}\)、ホイールの \(x_I\) 軸周りの角速度を \(\omega_\text{wheel} > 0\)、アームの \(y_I\) 軸周りの角速度を \(\omega_\text{arm}\) とすれば、式(1)を参照して、ホイールの \(z_I\) 軸周りのジャイロモーメントが次式で与えられます。
$$ M_\text{gyro} = I_\text{wheel}\cdot\omega_\text{wheel}\cdot\omega_\text{arm} \tag{2}$$
式(2)より、\(\omega_\text{arm} > 0\) の時、つまりアームが右に回転する時、\(M_\text{gyro} > 0\) ですから、\(z_I\) 軸が水平より下向きの場合、ステージは上から見て右回りにモーメントを受けます。逆に、\(\omega_\text{arm} < 0\) の時、つまりアームが左に回転する時、\(M_\text{gyro} < 0\) ですから、\(z_I\) 軸が水平より下向きの場合、ステージは上から見て左回りにモーメントを受けます。
この機械モデルの動力学シミュレーション結果のアニメーションを以下に示します。
ジャイロモーメントの導出
式(1)のジャイロモーメントを導出してみましょう。
角速度の関係式
剛体の角速度ベクトルの全体座標系(慣性座標系)と座標系 \(O-x_I y_I z_I\) による成分表示をそれぞれ \(\boldsymbol{\omega}, \boldsymbol{\omega}^{(I)}\) とし、全体座標系に対する座標系 \(O-x_I y_I z_I\) の回転行列を \(\mathbf{R}_I\) とすれば、以下の関係式が成り立ちます。
$$\boldsymbol{\omega}=\mathbf{R}_{I}\boldsymbol{\omega}^{(I)} \tag{3}$$
$$\tilde{\boldsymbol{\omega}}=\mathbf{R}_{I}\tilde{\boldsymbol{\omega}}^{(I)}\mathbf{R}_{I}^T \tag{4}$$
ここで、記号「~」はチルダオペレータです。式(3)(4)の導出およびチルダオペレータについては、ベクトルの成分表示と座標変換【力学の道具箱】を参照してください。
座標系 \(O-x_I y_I z_I\) の角速度ベクトルの自身による成分表示を \(\boldsymbol{\omega}_I^{(I)}\equiv\begin{bmatrix}0 & \omega_{y_I} & \omega_{z_I}\end{bmatrix}^T\)(定義より \(x_I\) 方向成分は \(0\))、座標系 \(O-x_I y_I z_I\) に対する剛体の \(x_I\) 軸周りの相対角速度を \(\Omega\) とすれば、以下の関係式が成り立ちます。
$$\boldsymbol{\omega}^{(I)}=\boldsymbol{\omega}_{I}^{(I)}+\begin{bmatrix}\Omega\\0\\0\end{bmatrix} \tag{5}$$
$$\boldsymbol{\omega}_{I}^{(I)}=\boldsymbol{\omega}^{(I)}-\begin{bmatrix}\Omega\\0\\0\end{bmatrix} \tag{6}$$
また、ポアソンの微分方程式より、
$$\dot{\mathbf{R}}_{I}=\mathbf{R}_{I}\tilde{\boldsymbol{\omega}}_{I}^{(I)} \tag{7}$$
が成り立ちます。
さらに、式(3)を時間微分し、式(7)(6)を代入して整理すれば
$$
\begin{align}
\dot{\boldsymbol{\omega}}
&=\dot{\mathbf{R}}_{I}\boldsymbol{\omega}^{(I)}+\mathbf{R}_{I}\dot{\boldsymbol{\omega}}^{(I)}\\
&\underset{\text{(7)}}{=}\mathbf{R}_{I}\tilde{\boldsymbol{\omega}}_{I}^{(I)}\boldsymbol{\omega}^{(I)}+\mathbf{R}_{I}\dot{\boldsymbol{\omega}}^{(I)}\\
&\underset{\text{(6)}}{=}\mathbf{R}_{I}\left(\tilde{\boldsymbol{\omega}}^{(I)}-\begin{bmatrix}\Omega\\0\\0\end{bmatrix}^{\sim}\right)\boldsymbol{\omega}^{(I)}+\mathbf{R}_{I}\dot{\boldsymbol{\omega}}^{(I)}\\
&=-\mathbf{R}_{I}\begin{bmatrix}\Omega\\0\\0\end{bmatrix}^{\sim}\boldsymbol{\omega}^{(I)}+\mathbf{R}_{I}\dot{\boldsymbol{\omega}}^{(I)} \tag{8}\\
\end{align}
$$
を得ます。ここで、最後の等号は自身の外積が零ベクトルであること(\(\tilde{\boldsymbol{\omega}}^{(I)}\boldsymbol{\omega}^{(I)}=\mathbf{0}\))を用いています。
中間座標系による回転運動方程式
軸対称剛体の回転運動方程式は、オイラーの運動方程式(全体座標系による表現)より
$$\mathbf{I}\dot{\boldsymbol{\omega}}+\tilde{\boldsymbol{\omega}}\mathbf{I}\boldsymbol{\omega}=\mathbf{M} \tag{9}$$
で与えられます。ここで、\(\mathbf{I}\) は剛体の慣性行列、\(\mathbf{M}\) は剛体に働く力のモーメントです。
この回転運動方程式を座標系 \(O-x_I y_I z_I\) による表現に変換します。
式(9)に式(3)(4)(8)を代入し、
$$-\mathbf{I}\mathbf{R}_{I}\begin{bmatrix}\Omega\\0\\0\end{bmatrix}^{\sim}\boldsymbol{\omega}^{(I)}+\mathbf{I}\mathbf{R}_{I}\dot{\boldsymbol{\omega}}^{(I)}+\mathbf{R}_{I}\tilde{\boldsymbol{\omega}}^{(I)}\mathbf{R}_{I}^T\mathbf{I}\mathbf{R}_{I}\boldsymbol{\omega}^{(I)}=\mathbf{M}$$
左から \(\mathbf{R}_I^T\) を掛ければ、
$$-\mathbf{R}_{I}^T\mathbf{I}\mathbf{R}_{I}\begin{bmatrix}\Omega\\0\\0\end{bmatrix}^{\sim}\boldsymbol{\omega}^{(I)}+\mathbf{R}_{I}^T\mathbf{I}\mathbf{R}_{I}\dot{\boldsymbol{\omega}}^{(I)}+\tilde{\boldsymbol{\omega}}^{(I)}\mathbf{R}_{I}^T\mathbf{I}\mathbf{R}_{I}\boldsymbol{\omega}^{(I)}=\mathbf{R}_{I}^T\mathbf{M} \tag{10}$$
を得ます。
座標系 \(O-x_{I}y_{I}z_{I}\) による慣性行列と力のモーメントをそれぞれ \(\mathbf{I}^{(I)}, \mathbf{M}^{(I)}\) とすると
$$\mathbf{I}^{(I)}=\mathbf{R}_{I}^T\mathbf{I}\mathbf{R}_{I},\quad \mathbf{M}^{(I)}=\mathbf{R}_{I}^T\mathbf{M}$$
ですから、式(10)より
$$\mathbf{I}^{(I)}\dot{\boldsymbol{\omega}}^{(I)}+\tilde{\boldsymbol{\omega}}^{(I)}\mathbf{I}^{(I)}\boldsymbol{\omega}^{(I)}-\mathbf{I}^{(I)}\begin{bmatrix}\Omega\\0\\0\end{bmatrix}^{\sim}\boldsymbol{\omega}^{(I)}=\mathbf{M}^{(I)} \tag{11}$$
を得ます。これが、剛体の回転運動方程式の座標系 \(O-x_I y_I z_I\) による表現です。
次に、式(11)を成分で書き下してみましょう。剛体の対称軸周りの慣性モーメントを \(I_a\)、点 \(O\) を通り対称軸に垂直な軸周りの慣性モーメントを \(I_t\) とすると、座標系 \(O-x_{I}y_{I}z_{I}\) による剛体の慣性行列は
$$
\mathbf{I}^{(I)} =
\begin{bmatrix}
I_a & 0 & 0\\
0 & I_t & 0\\
0 & 0 & I_t\\
\end{bmatrix} \tag{12}
$$
です。また、式(5)より、\(\boldsymbol{\omega}^{(I)}\) の成分は
$$
\boldsymbol{\omega}^{(I)} =
\begin{bmatrix}
\Omega \\ \omega_{y_I} \\ \omega_{z_I} \tag{13}\\
\end{bmatrix}
$$
です。
式(12)(13)を用いれば、
$$
\mathbf{I}^{(I)}\dot{\boldsymbol{\omega}}^{(I)}=
\begin{bmatrix}
I_a\dot{\Omega} \\ I_t\dot{\omega}_{y_I} \\ I_t\dot{\omega}_{z_I} \\
\end{bmatrix}
$$
$$
\tilde{\boldsymbol{\omega}}^{(I)}\mathbf{I}^{(I)}\boldsymbol{\omega}^{(I)}=
\begin{bmatrix}
0 \\ (I_a-I_t)\Omega\omega_{z_I} \\ (I_t-I_a)\Omega\omega_{y_I} \\
\end{bmatrix}
$$
$$
-\mathbf{I}^{(I)}\begin{bmatrix}\Omega\\0\\0\end{bmatrix}^{\sim}\boldsymbol{\omega}^{(I)}=
\begin{bmatrix}
0 \\ I_t\Omega\omega_{z_I} \\ -I_t\Omega\omega_{y_I} \\
\end{bmatrix}\\
$$
ですから、これらを式(11)に代入し
$$
\begin{bmatrix}
I_a\dot{\Omega} \\ I_t\dot{\omega}_{y_I} \\ I_t\dot{\omega}_{z_I} \\
\end{bmatrix}
+
\begin{bmatrix}
0 \\ (I_a-I_t)\Omega\omega_{z_I} \\ (I_t-I_a)\Omega\omega_{y_I} \\
\end{bmatrix}
+
\begin{bmatrix}
0 \\ I_t\Omega\omega_{z_I} \\ -I_t\Omega\omega_{y_I} \\
\end{bmatrix}
=
\mathbf{M}^{(I)}
$$
整理すれば、
$$
\begin{bmatrix}
I_a\dot{\Omega} \\ I_t\dot{\omega}_{y_I} \\ I_t\dot{\omega}_{z_I} \\
\end{bmatrix}
=
\mathbf{M}^{(I)}
+
\underbrace{
\begin{bmatrix}
0 \\ -I_a\Omega\omega_{z_I} \\ I_a\Omega\omega_{y_I} \\
\end{bmatrix}
}_{\mathbf{M}_\text{gyro}^{(I)}} \tag{14}
$$
を得ます。式(14)の右辺第2項が、式(1)のジャイロモーメントを表します。
独楽が倒れない理由
独楽は、歳差運動(回転軸が円錐を描くように振れ回る運動)と章動(対称軸の傾角の振動)をしながら、重力に逆らって立っている状態を保ちます。歳差運動や章動が生じる理由、そして独楽が倒れない理由はジャイロモーメントによって説明することができます。
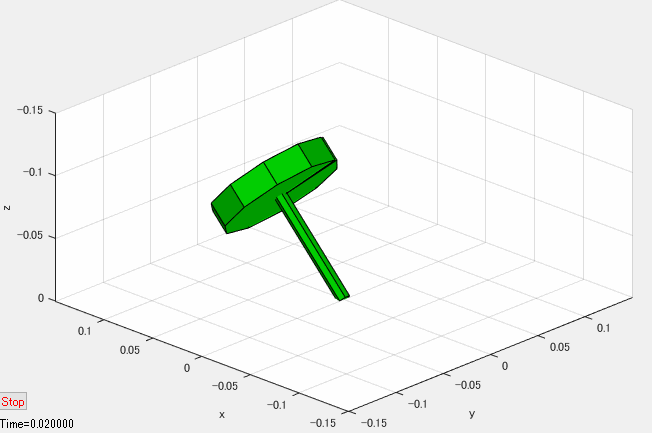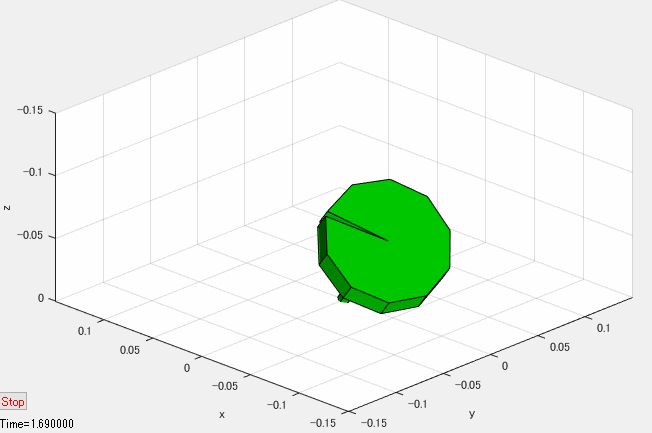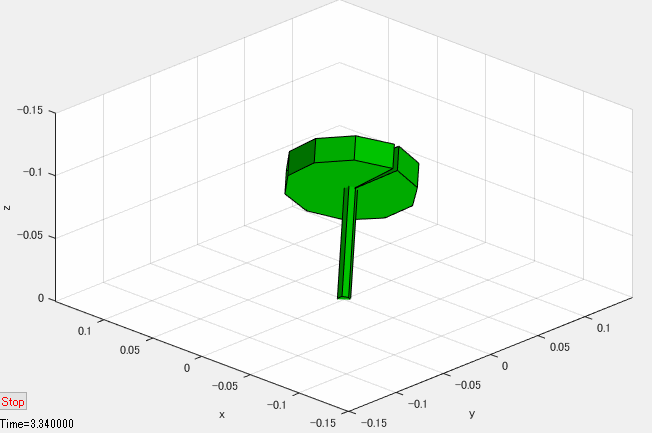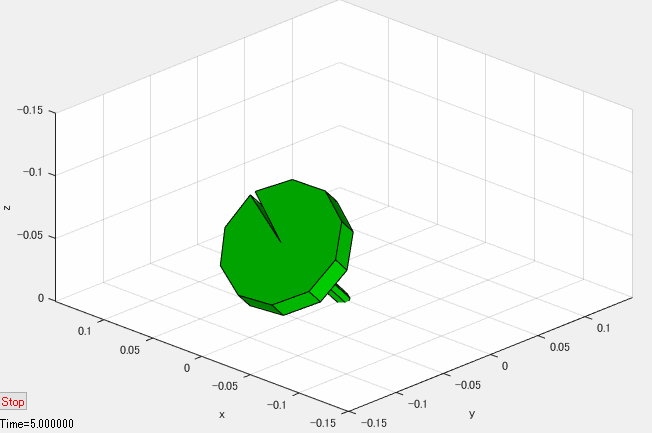
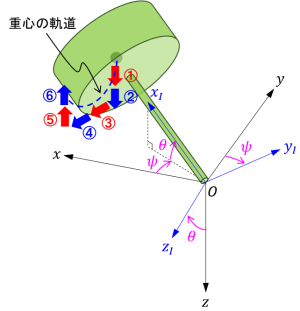
下図のように、慣性系に固定された座標系 \(O-xyz\)(\(z\) 軸下向き)と、点 \(O\) を支点して回転する独楽を考えます。
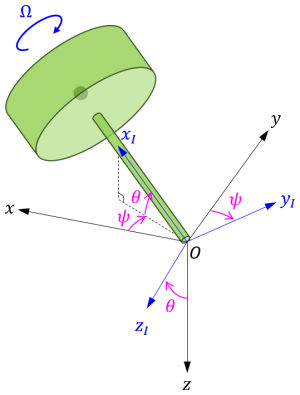
慣性座標系 \(O-xyz\) に対するオイラー角(zyx)が \(\left(\psi, \theta, 0\right)\) の中間座標系 \(O-x_{I}y_{I}z_{I}\) を考えます。座標系 \(O-x_{I}y_{I}z_{I}\) は \(x_{I}\) 軸が独楽の対称軸と一致しますが、対称軸周りには回転しないような座標系です。
さて、独楽が上図のような状態で、\(x_I\) 軸周りに角速度 \(\Omega > 0\) で回転している時、次の①~⑥が連鎖的に生じます。
- ① \(y_I\) 軸左回りに重力モーメントが働く
- ② \(y_I\) 軸左回りに角速度が生じる(\(\omega_{y_I}<0 \Rightarrow \dot{\theta}<0\))
- ③ \(z_I\) 軸左回りにジャイロモーメントが働く(\(M_{z_I}=I_a\Omega\omega_{y_I}<0\))
- ④ \(z_I\) 軸左回りに角速度が生じる(\(\omega_{z_I}<0 \Rightarrow \dot{\psi}<0\))
- ⑤ \(y_I\) 軸右回りにジャイロモーメントが働く(\(M_{y_I}=-I_a\Omega\omega_{z_I}>0\))
- ⑥ \(y_I\) 軸右回りに角速度が生じる(\(\omega_{y_I}>0 \Rightarrow \dot{\theta}>0\))
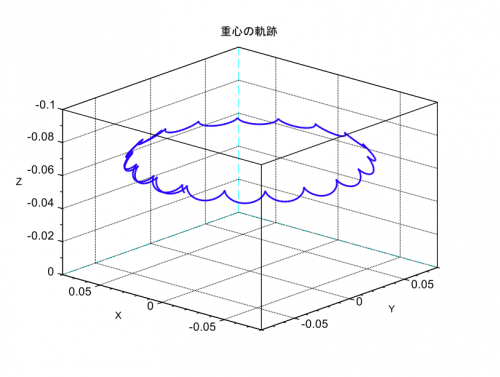
これにより、独楽の重心は下図のような軌道を描きます。④は歳差運動、②⑥は章動となります。
すなわち、重力によって独楽が倒れようとすると、倒れる方向の角速度に起因するジャイロモーメントによって、独楽は歳差運動を始めます。さらに、独楽が歳差運動をすると、歳差運動の角速度に起因するジャイロモーメントによって、独楽が起きる方向に押されるのです。つまり、重力による独楽を倒そうとするモーメントと、歳差運動に起因する独楽を起こそうとするジャイロモーメントが均衡し、独楽は倒れないのです。
まとめ
この記事では、剛体の回転運動に伴う、ジャイロモーメントと呼ばれる見かけのモーメントについて解説し、また、ジャイロモーメントによって独楽が倒れない理由を説明できることを示しました。独楽の運動に見られるようなジャイロモーメントの効果はジャイロ効果(gyroscopic effect)と呼ばれ、回転部分を持つ機械(バイク、ヘリコプターなど)でしばしば現れます。ジャイロ効果は、機械の目的や場面によって、安定性を増すなどの好影響を与える場合もあれば、外乱や負荷となり悪影響を与える場合もあります。また、ジャイロ効果を積極的に利用する機械(ジャイロスコープ、ジャイロアクチュエータなど)もあります。
最後まで読んでいただきありがとうございました。この記事がご参考になれば幸いです。


コメント