回転行列(方向余弦行列)は、3次元または2次元空間における“回転”または“回転姿勢”を表す便利な行列で、力学やコンピュータグラフィックスでよく使われています。この記事では、回転行列の定義と性質、3つの物理的な意味、そしていくつかの有用な公式をまとめてみました。なお、対象は3次元の回転行列ですが、多くの結果は2次元の回転行列へも適用できます。
回転行列の定義
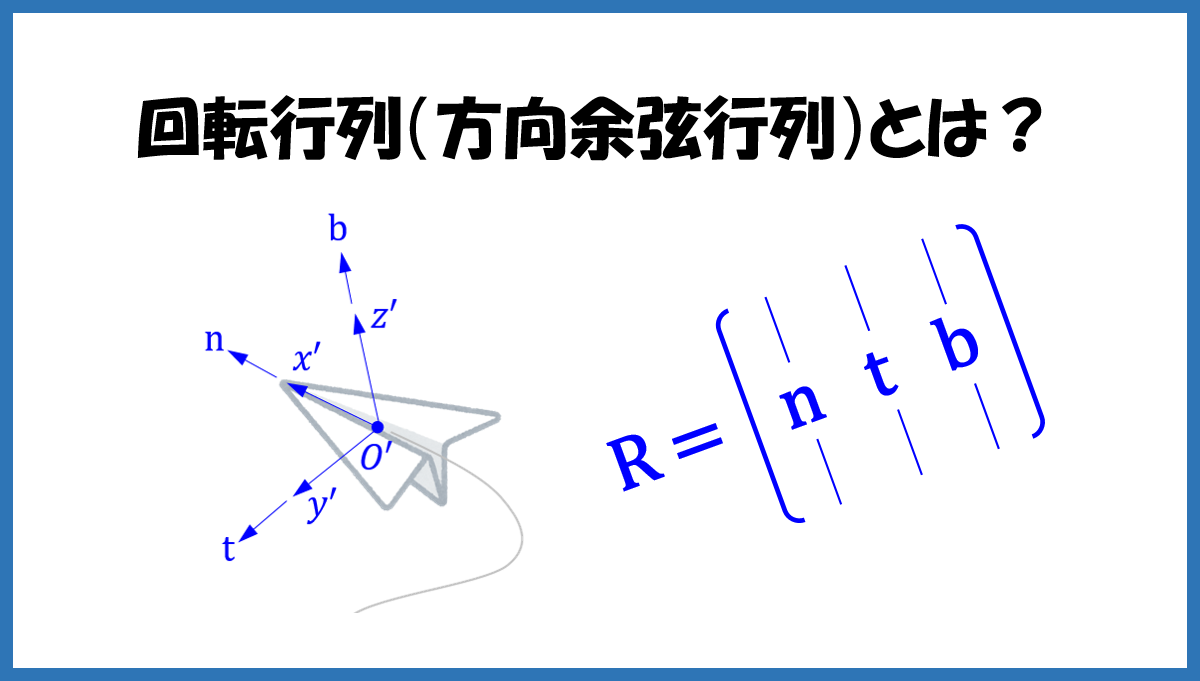
下図において、\(O-xyz\) は地上に固定された基準座標系であるとします。飛行機が飛行によって地上に対する位置と向き(回転姿勢)を変えるとき、ある瞬間の飛行機の向き(回転姿勢)は、飛行機に固定された座標系 \(O^{\prime}-x^{\prime}y^{\prime}z^{\prime}\) の座標軸の向きで示すことができます。
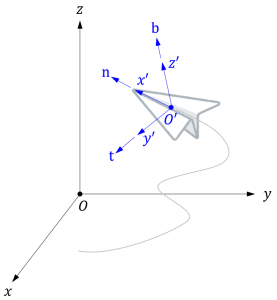
そこで、\(x^{\prime}\) 軸、\(y^{\prime}\) 軸、\(z^{\prime}\) 軸方向の単位ベクトル(基準座標系 \(O-xyz\) による成分の列ベクトル)をそれぞれ \(\mathbf{n}\)、 \(\mathbf{t}\)、 \(\mathbf{b}\) とし、次のような行列 \(\mathbf{R}\) を作れば、この行列は飛行機の向き(回転姿勢)を完全に特定します。
$$\mathbf{R}=\begin{bmatrix} \mathbf{n} & \mathbf{t} & \mathbf{b} \end{bmatrix}$$
この \(3\times 3\) 行列 \(\mathbf{R}\) を回転行列(方向余弦行列)と呼びます[2]。行列 \(\mathbf{R}\) は点 \(O^{\prime}\) の位置には依らず、純粋に座標系 \(O^{\prime}-x^{\prime}y^{\prime}z^{\prime}\) の向き(回転姿勢)の情報だけを持っている点に注目してください。
回転行列の性質
正規直交性
行列 \(\mathbf{R}\) の列ベクトル \(\mathbf{n}\)、\(\mathbf{t}\)、\(\mathbf{b}\) はそれぞれ座標軸方向の単位ベクトルですから、互いに直交し、大きさは1です。従って、次の6つの式を満たします。
$$\begin{array}{ccc}\mathbf{n}^{T}\mathbf{t}=0, & \mathbf{t}^{T}\mathbf{b}=0, & \mathbf{b}^{T}\mathbf{n}=0,\\ \mathbf{n}^{T}\mathbf{n}=1, & \mathbf{t}^{T}\mathbf{t}=1, & \mathbf{b}^{T}\mathbf{b}=1\end{array}\tag{1}$$
ここで、上付きの \(T\) は行列の転置を表します。行列 \(\mathbf{R}\) とその転置行列 \(\mathbf{R}^{T}\) の積は
$$\mathbf{R}^{T}\mathbf{R}=\mathbf{R}\mathbf{R}^{T}=\begin{bmatrix} \mathbf{n}^{T}\mathbf{n} & \mathbf{n}^{T}\mathbf{t} & \mathbf{n}^{T}\mathbf{b} \\ \mathbf{t}^{T}\mathbf{n} & \mathbf{t}^{T}\mathbf{t} & \mathbf{t}^{T}\mathbf{b} \\ \mathbf{b}^{T}\mathbf{n} & \mathbf{b}^{T}\mathbf{t} & \mathbf{b}^{T}\mathbf{b} \end{bmatrix}=\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \equiv \mathbf{I}$$
と単位行列になりますので、\(\mathbf{R}^T\) は \(\mathbf{R}\) の逆行列であることが分かります。
$$\mathbf{R}^{-1}=\mathbf{R}^{T}\tag{2}$$
自身の転置が自身の逆行列になるような行列は、正規直交行列と呼ばれています[2]。
必要十分条件
全ての正規直交行列が回転行列になり得るかというと、実はそうではありません。例えば、次の行列は正規直交行列ですが回転行列ではありません。
$$\mathbf{A}=\begin{bmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$$
この行列の列ベクトルは、\(y\) 軸が反転した座標系を形成しますが、回転のみによってこの座標系に到達することはできないからです。
任意の行列 \(\mathbf{R}\) が回転行列であるためには、正規直交行列であることに加え、行列式 \(\det{\mathbf{R}}\) が \(+1\) である必要があります[1]。
回転行列の積
行列 \(\mathbf{R}_1\) と \(\mathbf{R}_2\) がそれぞれ回転行列であるとき、その積 \(\mathbf{R}_1\mathbf{R}_2\) も回転行列になります[1]。これは、\(\mathbf{R}_1\mathbf{R}_2\) が正規直交行列かつ行列式が \(+1\) になることを示すことで証明できます。
回転行列の3つの物理的な意味
回転行列には3つの異なる物理的な意味があります[2]。
物理的意味①:剛体の回転姿勢を表す
冒頭の定義から明らかなように、回転行列は基準の座標系に対する剛体または剛体に固定された座標系の向き(回転姿勢)を表します。剛体の運動解析において、剛体に固定された座標系の回転行列 \(\mathbf{R}\) が時間の関数として与えられれば、各時刻における剛体の向き(回転姿勢)が与えられたことになります。
さて、回転行列 \(\mathbf{R}\) を自由に選んでよいとします。言い換えれば、飛行機を好きな方向へ向けてよいとします。この時、 \(\mathbf{R}\) の9個の成分を、(1) の6個の条件式が満たされるように選ばなければなりません。9個の変数に対して6個の条件式がありますから、自由に選ぶことができる独立変数の数は 9 – 6 = 3個になります。このことから、「拘束のない剛体の回転自由度は3」であることが分かります。
物理的意味②:座標変換を表す
空間内の任意のベクトル \( \vec{a} \) について、\(\vec{a}\) の座標系 \(O^{\prime}-x^{\prime}y^{\prime}z^{\prime}\) による成分表示を
$$ \mathbf{a}^{\prime}=\begin{bmatrix} a_{x}^{\prime} \\ a_{y}^{\prime} \\ a_{z}^{\prime} \end{bmatrix} $$
とすると、\(\vec{a}\) の座標系 \(O-xyz\) による成分表示は、\(\mathbf{n}\)、\(\mathbf{t}\)、\(\mathbf{b}\) を用いて次のように求めることができます。
$$ \mathbf{a}=a_{x}^{\prime}\mathbf{n}+a_{y}^{\prime}\mathbf{t}+a_{z}^{\prime}\mathbf{b} $$
上式の右辺は
$$ a_{x}^{\prime}\mathbf{n}+a_{y}^{\prime}\mathbf{t}+a_{z}^{\prime}\mathbf{b}=\begin{bmatrix} \mathbf{n} & \mathbf{t} & \mathbf{b} \end{bmatrix}\begin{bmatrix} a_{x}^{\prime} \\ a_{y}^{\prime} \\ a_{z}^{\prime} \end{bmatrix}=\mathbf{R}\mathbf{a}^{\prime} $$
と変形できるので、結局
$$ \mathbf{a}=\mathbf{R}\mathbf{a}^{\prime} \tag{3} $$
が成り立ちます。
式(3)は、回転行列 \(\mathbf{R}\) によって、任意のベクトルの座標系 \(O^{\prime}-x^{\prime}y^{\prime}z^{\prime}\) による成分表示を、座標系 \(O-xyz\) による成分表示に変換できることを示しています。
さらに、式(3)の両辺に \(\mathbf{R}^{T}\) を左側から掛け、式(2)を用いれば、
$$\mathbf{R}^{T}\mathbf{a}=\mathbf{a}^{\prime}$$
となり、逆変換は \(\mathbf{R}^{T}\) で与えられることが分かります。
この物理的意味から、回転行列 \(\mathbf{R}\) とその転置行列 \(\mathbf{R}^{T}\) はしばしば座標変換行列と呼ばれます。
物理的意味③:ベクトルの回転を表す
剛体に固定され、剛体と共に移動する任意のベクトル \(\vec{a}\) を考えます。はじめ、基準座標系 \(O-xyz\) と剛体座標系 \(O^{\prime}-x^{\prime}y^{\prime}z^{\prime}\) が一致しているとし、このときの \(\vec{a}\) の基準座標系による成分表示を \(\mathbf{a}\) とします。その後、剛体が \(\mathbf{R}\) だけ回転すれば、ベクトル \(\vec{a}\) も剛体とともに回転し、 \(\vec{a}\) の基準座標系による成分表示は \(\mathbf{R}\mathbf{a}\) になります。すなわち、座標系 \(O-xyz\) における写像
$$ \mathbf{a}\mapsto\mathbf{Ra} $$
はベクトルの回転を表します。
上記の3つの物理的意味は、どの意味付けによって回転行列を定義しても他の2つを導けるので、等価です[2]。この記事では、物理的意味①によって回転行列を定義しました。
具体的な回転行列
では、具体的な回転行列を見てみましょう。回転行列は座標系の原点の位置には依らないので、一般性を失うことなく、座標系 \(O-xyz\) と座標系 \(O^{\prime}-x^{\prime}y^{\prime}z^{\prime}\) の原点が一致したケースで考えることができます。
座標軸周りの回転を表す回転行列
下図のように、\(z\) 軸周りの回転を表す回転行列を考えます[2]。
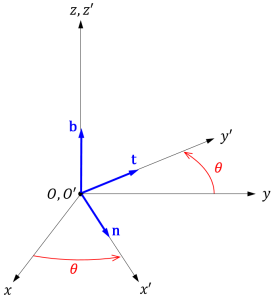
回転角を \(\theta\) (右ねじ回り)とすると、座標系 \(O^{\prime}-x^{\prime}y^{\prime}z^{\prime}\) の各軸方向の単位ベクトルは
$$ \mathbf{n}=\begin{bmatrix} \cos{\theta} \\ \sin{\theta} \\ 0 \end{bmatrix}, \quad \mathbf{t}=\begin{bmatrix} -\sin{\theta} \\ \cos{\theta} \\ 0 \end{bmatrix}, \quad \mathbf{b}=\begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} $$ですから、回転行列は$$ \mathbf{R}_z=\begin{bmatrix} \cos{\theta} & -\sin{\theta} & 0 \\ \sin{\theta} & \cos{\theta} & 0 \\ 0 & 0 & 1 \end{bmatrix} $$
となります。
同様に、\(x\) 軸、\(y\) 軸周りの回転を表す回転行列はそれぞれ
$$ \mathbf{R}_x=\begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos{\theta} & -\sin{\theta} \\ 0 & \sin{\theta} & \cos{\theta} \end{bmatrix}, \quad \mathbf{R}_y=\begin{bmatrix} \cos{\theta} & 0 & \sin{\theta} \\ 0 & 1 & 0 \\ -\sin{\theta} & 0 & \cos{\theta} \end{bmatrix} $$
となります。
任意の軸周りの回転を表す回転行列(ロドリゲスの公式)
下図のように、任意の軸周りの回転を表す回転行列を考えます。
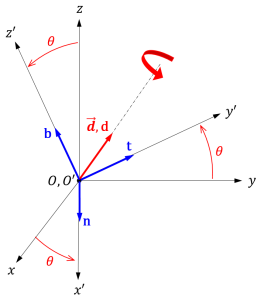
回転軸方向の単位ベクトルを \(\vec{d}\) とし、\(\vec{d}\) の基準座標系 \(O-xyz\) による成分表示を
$$ \mathbf{d}=\begin{bmatrix} d_x \\ d_y \\ d_z \end{bmatrix} $$
とします。また、回転角を \(\theta\) (右ねじ回り)とします。
座標系 \(O^{\prime}-x^{\prime}y^{\prime}z^{\prime}\)の軸方向の単位ベクトル \( \mathbf{n}\)、\(\mathbf{t}\)、\(\mathbf{b}\) を求めるために、まず、一般のベクトルがこの回転によってどのように移動するかを調べてみます。下図のように、ベクトル \(\vec{a}\) が回転によってベクトル \(\vec{a}^{\prime}\) に移動するとします。
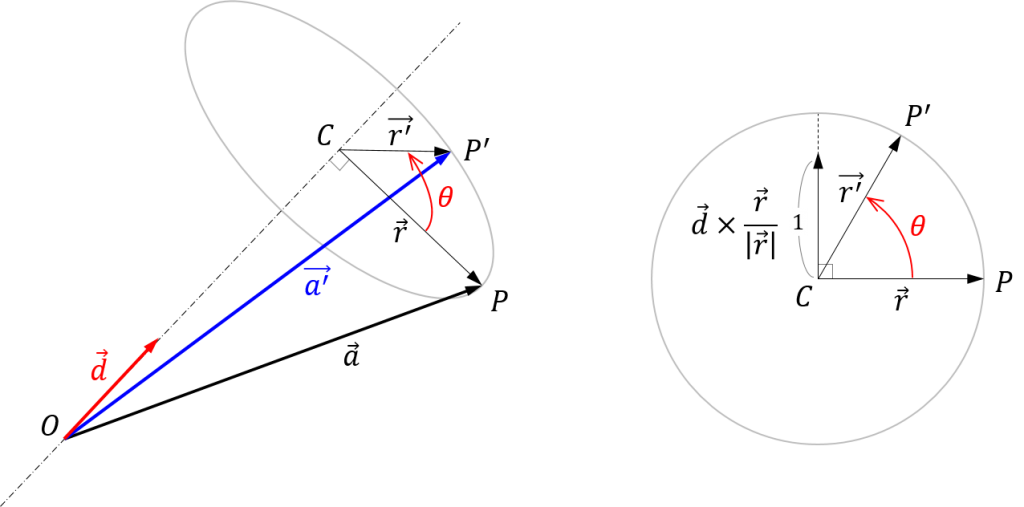
ベクトル \(\vec{a}\) 先端の回転円の中心を \(C\)、\(\vec{a}\) の先端を \(P\)、\(\vec{a}^{\prime}\) の先端を \(P^{\prime}\) とすると、以下のようにベクトル \(\vec{a}^{\prime}\) を求めることができます。
$$ \begin{align} \vec{r} &= \vec{OP}-\vec{OC} \\ &= \vec{a}-\left(\vec{a} \cdot \vec{d}\right)\vec{d} \tag{A} \end{align} $$
$$ \begin{align} \vec{r^{\prime}} &= \vec{CP^{\prime}} \\ &= |\vec{r}|\cos{\theta}\:\frac{\vec{r}}{|\vec{r}|}+|\vec{r}|\sin{\theta}\left(\vec{d}\times\frac{\vec{r}}{|\vec{r}|}\right) \\ &= \cos{\theta}\:\vec{r}+\sin{\theta}\left(\vec{d}\times\vec{r}\right) \\ &\underset{\text{(A)}}{=} \cos{\theta}\left[\vec{a}-\left(\vec{a} \cdot \vec{d}\right)\vec{d}\right]+\sin{\theta}\left(\vec{d}\times\vec{a}\right) \tag{B} \end{align} $$
$$ \begin{align} \vec{a}^{\prime} &= \vec{OC}+\vec{CP^{\prime}} \\ &= \left(\vec{a}\cdot\vec{d}\right)\vec{d}+\vec{r}^{\prime} \\ &\underset{\text{(B)}}{=} (1-\cos{\theta})\left(\vec{a} \cdot \vec{d}\right)\vec{d} + \cos{\theta}\:\vec{a} + \sin{\theta}\left(\vec{d}\times\vec{a}\right) \tag{C} \end{align} $$
式(C)において、ベクトル \(\vec{a}\) に \(x\)、\(y\)、\(z\) 軸方向の単位ベクトルを代入すれば、 \(x^{\prime}\)、\(y^{\prime}\)、\(z^{\prime}\) 軸方向の単位ベクトル \(\mathbf{n}\)、\(\mathbf{t}\)、\(\mathbf{b}\) をそれぞれ求めることができます。
$$ \begin{align} \mathbf{n} &= (1-\cos{\theta})\left( \begin{bmatrix} 1 & 0 & 0 \end{bmatrix} \begin{bmatrix} d_x \\ d_y \\ d_z \end{bmatrix} \right)\begin{bmatrix} d_x \\ d_y \\ d_z \end{bmatrix} + \cos{\theta}\begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} + \sin{\theta} \left(\begin{bmatrix} d_x \\ d_y \\ d_z \end{bmatrix}\times\begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}\right) \\ &= (1-\cos{\theta})d_x\begin{bmatrix} d_x \\ d_y \\ d_z \end{bmatrix} + \cos{\theta}\begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} + \sin{\theta}\begin{bmatrix} 0 \\ d_z \\ -d_y \end{bmatrix}, \end{align}$$
$$ \begin{align} \mathbf{t} &= (1-\cos{\theta})\left( \begin{bmatrix} 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} d_x \\ d_y \\ d_z \end{bmatrix} \right)\begin{bmatrix} d_x \\ d_y \\ d_z \end{bmatrix} + \cos{\theta}\begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix} + \sin{\theta}\left(\begin{bmatrix} d_x \\ d_y \\ d_z \end{bmatrix}\times\begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix}\right) \\ &= (1-\cos{\theta})d_y\begin{bmatrix} d_x \\ d_y \\ d_z \end{bmatrix} + \cos{\theta}\begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix} + \sin{\theta}\begin{bmatrix} -d_z \\ 0 \\ d_x \end{bmatrix}, \end{align}$$
$$ \begin{align} \mathbf{b} &= (1-\cos{\theta})\left( \begin{bmatrix} 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} d_x \\ d_y \\ d_z \end{bmatrix} \right)\begin{bmatrix} d_x \\ d_y \\ d_z \end{bmatrix} + \cos{\theta}\begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} + \sin{\theta}\left(\begin{bmatrix} d_x \\ d_y \\ d_z \end{bmatrix}\times\begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}\right) \\ &= (1-\cos{\theta})d_z\begin{bmatrix} d_x \\ d_y \\ d_z \end{bmatrix} + \cos{\theta}\begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} + \sin{\theta}\begin{bmatrix} d_y \\ -d_x \\ 0 \end{bmatrix} \end{align}$$
従って、回転行列は次のようになります[3]。
$$ \begin{align} \mathbf{R} &= \begin{bmatrix} {d_x}^2(1-\cos{\theta})+\cos{\theta} & {d_x}{d_y}(1-\cos{\theta})-d_z\sin{\theta} & {d_x}{d_z}(1-\cos{\theta})+d_y\sin{\theta} \\ {d_y}{d_x}(1-\cos{\theta})+d_z\sin{\theta} & {d_y}^2(1-\cos{\theta})+\cos{\theta} & {d_y}{d_z}(1-\cos{\theta})-d_x\sin{\theta} \\ {d_z}{d_x}(1-\cos{\theta})-d_y\sin{\theta} & {d_z}{d_y}(1-\cos{\theta})+d_x\sin{\theta} & {d_z}^2(1-\cos{\theta})+\cos{\theta} \end{bmatrix} \tag{4} \\ \\ &= \mathbf{d}\mathbf{d}^T(1-\cos{\theta})+\mathbf{I}\cos{\theta}+\tilde{\mathbf{d}}\sin{\theta} \end{align} $$
ここで、\(\tilde{\mathbf{d}}\) は歪対称行列
$$\tilde{\mathbf{d}} = \begin{bmatrix} 0 & -d_z & d_y \\ d_z & 0 & -d_x \\ -d_y & d_x & 0 \end{bmatrix} $$
です。
オイラーの定理および回転軸と回転角
剛体回転に関するオイラーの定理は、「一点が固定された剛体において、固定点周りのどのような回転変位も、その固定点を通るある軸周りの一回の回転によって到達できる」ことを保証しています[1]。これはすなわち、どのような回転行列で表される回転も、一つの軸周りの回転として表すことができるということです。
前項では、任意の軸周りの回転について、回転軸方向ベクトル \(\mathbf{d}\) と回転角 \(\theta\) から回転行列 \(\mathbf{R}\) を求める公式を示しました。逆に、回転行列 \(\mathbf{R}\) が与えられたとき、同等な軸周り回転の回転軸方向ベクトル \(\mathbf{d}\) と回転角 \(\theta\) を、以下の式によって求めることができます[1]。
$$ \cos{\theta} = \frac{\text{tr}\mathbf{R}-1}{2}, \tag{5} $$
$$ \mathbf{d} = \frac{1}{2\sin{\theta}} \begin{bmatrix} R_{32}-R_{23} \\ R_{13}-R_{31} \\ R_{21}-R_{12} \end{bmatrix} \tag{6} $$
ここで、\(\text{tr}\mathbf{R}\) は \(\mathbf{R}\) のトレース(対角成分の和)、\(R_{ij}\) は \(\mathbf{R}\) の \((i,j)\) 成分です。回転角 \(\theta\) を \(0\leq\theta\leq\pi\) の範囲で求めれば、方向ベクトルに対して右回りの回転が得られます。式(5)、(6)は、式(4)から容易に導かれます。
式(6)は、しかしながら、分母に \(\sin{\theta}\) を含んでいるので、 \(\sin{\theta}\) がごく小さいとき( \(\theta\) が \(0\)または \(\pi\) にごく近いとき)には、計算結果が不正確になる可能性があります。そこで、式(6) の代わりに、次式を用いることもできます[1]。
$$ \mathbf{d} = \frac{1}{l} \begin{bmatrix} R_{32}-R_{23} \\ R_{13}-R_{31} \\ R_{21}-R_{12} \end{bmatrix}, \tag{7} $$
$$ l^2 = (R_{32}-R_{23})^2 + (R_{13}-R_{31})^2 + (R_{21}-R_{12})^2 \tag{8}$$
またこの時、式(5)の変わりに、次式を用いて回転角を求めることもできます[1]。
$$ \sin{\theta} = \frac{l}{2} \tag{9} $$
式(7)、(8)、(9)も、式(4)から容易に導くことができます。
回転軸の方向ベクトルは、次項に示すように固有値問題を解くことによって求めることもできます。
回転行列の固有値と固有ベクトル
一般に、正方行列 \(\mathbf{R}\) に対し、
$$ \mathbf{R}\mathbf{x} = \lambda\mathbf{x} \tag{10} $$
を満たすスカラー \(\lambda\) とベクトル \(\mathbf{x}\) を求める問題は、固有値問題として知られています。固有値問題の解 \(\lambda\)、\(\mathbf{x}\) は、それぞれ \(\mathbf{R}\) の固有値、固有ベクトルと呼ばれます。
行列 \(\mathbf{R}\) が回転行列のとき、式(10)の左辺はベクトル \(\mathbf{x}\) の回転、右辺はベクトル \(\mathbf{x}\) の伸縮を表します。回転によってベクトルは伸縮しないので、\(|\lambda|=1\) です。
前項では、回転行列に対応する回転軸が存在し、その方向ベクトルを求めることができることを示しました。そこで、回転行列 \(\mathbf{R}\) の回転軸の方向ベクトルを \(\mathbf{d}\) とすると、\(\mathbf{d}\) は回転によって変化しないので、
$$ \mathbf{R}\mathbf{d} = \mathbf{d} \tag{11} $$
が成り立ちます。式(10)と式(11)を比較すると、\(+1\) は回転行列 \(\mathbf{R}\) の固有値であり、固有値 \(+1\) に対応する固有ベクトルは \(\mathbf{d}\) であることが分かります。
従って、回転行列の固有値問題(式(10))を解くことによっても、回転軸の方向ベクトルを求めることができます[1]。
連続回転の回転行列
下図のように、座標系 \(O^1-x^1y^1z^1\) が座標系 \(O^0-x^0y^0z^0\) に対して \(\mathbf{R}^{01}\) だけ回転、また座標系 \(O^2-x^2y^2z^2\) が座標系 \(O^1-x^1y^1z^1\) に対して \(\mathbf{R}^{12}\) だけ回転しているとします。
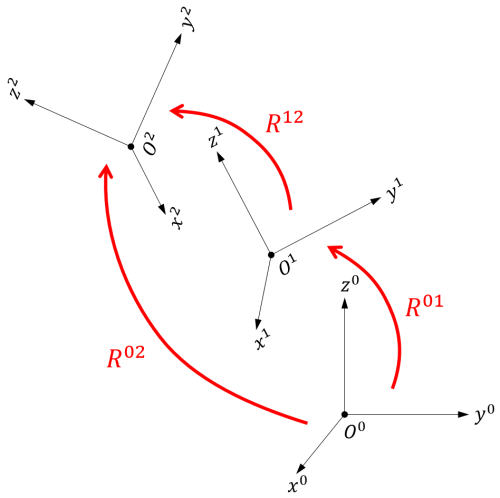
このとき、回転行列 \(\mathbf{R}^{12}\) の定義は2通り考えられます。1つは元の座標系 \(O^0-x^0y^0z^0\) を基準とした回転行列 \(\mathbf{R}_0^{12}\)、もう1つは座標系 \(O^1-x^1y^1z^1\) を基準とした回転行列 \(\mathbf{R}_1^{12}\) です。もちろん一般的に \(\mathbf{R}_0^{12} \ne \mathbf{R}_1^{12}\) です。
さて、座標系 \(O^2-x^2y^2z^2\) の座標系 \(O^0-x^0y^0z^0\) に対する回転を表す回転行列 \(\mathbf{R}^{02}\) は次のように計算できます[4]。
$$ \mathbf{R}^{02} = \mathbf{R}_0^{12}\mathbf{R}^{01} = \mathbf{R}^{01}\mathbf{R}_1^{12} \tag{12} $$
右辺の積の順序は重要です。
無限小回転の回転行列
式(4)において \(\theta\) が微小であるとき、\(\sin{\theta}\approx\theta\)、\(\cos{\theta}\approx 1\) ですから、無限小回転の回転行列は
$$ \mathbf{R}=\mathbf{I}+\tilde{\mathbf{d}}\theta $$
で与えられます[4]。
連続した無限小回転 \(\mathbf{R}_1\)、\(\mathbf{R}_2\) を考えます。
$$ \mathbf{R}_1=\mathbf{I}+\tilde{\mathbf{d}_1}\theta_1, \quad \mathbf{R}_2=\mathbf{I}+\tilde{\mathbf{d}_2}\theta_2 $$
すると、式(12)より、
$$ \mathbf{R}_1 \mathbf{R}_2 = (\mathbf{I}+\tilde{\mathbf{d}_1}\theta_1)(\mathbf{I}+\tilde{\mathbf{d}_2}\theta_2) = \mathbf{I}+\tilde{\mathbf{d}_1}\theta_1+\tilde{\mathbf{d}_2}\theta_2+\tilde{\mathbf{d}_1}\tilde{\mathbf{d}_2}\theta_1\theta_2 $$
となり、微小量 \(\theta_1\)、\(\theta_2\) の2次項を無視すると
$$ \mathbf{R}_1 \mathbf{R}_2 = \mathbf{I}+\tilde{\mathbf{d}_1}\theta_1+\tilde{\mathbf{d}_2}\theta_2 = \mathbf{R}_2 \mathbf{R}_1 $$
が得られます。これは、無限小回転においては、異なる軸周りの回転を足し合わせることができ、また回転の順序は無意味になることを示しています[4]。
数値例
上で紹介した結果のいくつかを確認する MATLAB スクリプトです。
% 回転軸の方向ベクトル
d = [sqrt(3)/2; 1/2; 0]
norm_d = norm(d) % dは単位ベクトル
% 回転角
theta = pi/4
% ロドリゲスの公式により回転行列を求める
R = rodrig(d(1), d(2), d(3), theta)
% Rが正規直交行列であることを確認
R_RT = R*R'
RT_R =R'*R
% Rの行列式が+1であることを確認
detR = det(R)
% Rから回転軸の方向ベクトルと回転角を復元
[d1, theta1] = simplerot1(R)
[d2, theta2] = simplerot2(R)
% 回転軸の方向ベクトルは固有値問題の解としても得られることを確認
[V, D] = eig(R)
% 式(4)により、回転軸の方向ベクトルと回転角から回転行列を求める関数
function R = rodrig(dx, dy, dz, theta)
d = [dx; dy; dz];
d = d/norm(d);
R = d*d'*(1-cos(theta)) + eye(3)*cos(theta) + skew(d)*sin(theta);
end
% ベクトルを歪対称行列に変換する関数
function a_tilda = skew(a)
a_tilda = [
0 -a(3) a(2);
a(3) 0 -a(1);
-a(2) a(1) 0;
];
end
% 式(5)(6)により、回転行列から回転軸の方向ベクトルと回転角を求める関数
function [d, theta] = simplerot1(R)
theta = acos((trace(R)-1)/2);
d = 1/2/sin(theta)*[R(3,2)-R(2,3); R(1,3)-R(3,1); R(2,1)-R(1,2)];
end
% 式(7)(8)(9)により、回転行列から回転軸の方向ベクトルと回転角を求める関数
function [d, theta] = simplerot2(R)
L = sqrt((R(3,2)-R(2,3))^2 + (R(1,3)-R(3,1))^2 + (R(2,1)-R(1,2))^2);
d = 1/L*[R(3,2)-R(2,3); R(1,3)-R(3,1); R(2,1)-R(1,2)];
theta = asin(L/2);
end
以下は、MATLAB R2017b による実行結果です。
d =
0.8660
0.5000
0
norm_d =
1
theta =
0.7854
R =
0.9268 0.1268 0.3536
0.1268 0.7803 -0.6124
-0.3536 0.6124 0.7071
R_RT =
1.0000 0 0
0 1.0000 0.0000
0 0.0000 1.0000
RT_R =
1.0000 0 0
0 1.0000 -0.0000
0 -0.0000 1.0000
detR =
1
d1 =
0.8660
0.5000
0
theta1 =
0.7854
d2 =
0.8660
0.5000
0
theta2 =
0.7854
V =
0.8660 + 0.0000i -0.0000 + 0.3536i -0.0000 - 0.3536i
0.5000 + 0.0000i 0.0000 - 0.6124i 0.0000 + 0.6124i
-0.0000 + 0.0000i -0.7071 + 0.0000i -0.7071 + 0.0000i
D =
1.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i
0.0000 + 0.0000i 0.7071 + 0.7071i 0.0000 + 0.0000i
0.0000 + 0.0000i 0.0000 + 0.0000i 0.7071 - 0.7071i
参考文献
[1] Greenwood, D.T. Principles of Dynamics. 2nd edition, Prentice Hall, 1988.
[2] Asada, H.; Slotine, J.-J. E. Robot Analysis and Control, John Wiley & Sons, 1986.
[3] 日本ロボット学会編. 新版ロボット工学ハンドブック, コロナ社, 2005.
[4] Shabana, A. A. Dynamics of Multibody Systems. 4th edition, Cambridge, 2013.





コメント