柔軟マルチボディダイナミクスの解法－浮動基準枠法

前回の記事で、マルチボディダイナミクスの定式化と解法について、平面（２次元）の剛体マルチボディシステムを例として解説しました。

マルチボディシステムの各物体（部品）は剛体として扱うことが多いですが、場合によっては一部の物体（部品）を可変形体として扱いたいときもあります。例えば、物体の弾性変形が無視できない場合や、ロープなどそもそも柔軟な部品をモデル化したい場合です。

この記事では、マルチボディダイナミクスで可変形体を扱う方法の一つ「浮動基準枠法」を紹介します。今回も平面（２次元）のマルチボディシステムを対象として解説します。

剛体 vs 可変形体

剛体とは時間によって形が変わらない物体、より正確には、物体内のどの２点間の距離も時間によって変わらない仮想的な物体です。

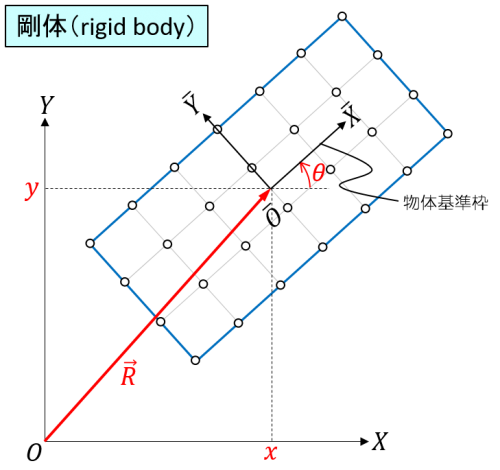
物体基準枠を剛体に固定すれば、物体基準枠に対する剛体中の各点の位置は不変なので、ある時点における剛体中のすべての点の位置は物体基準枠の位置 \(\mathbf{R} := \begin{bmatrix}x & y\end{bmatrix}^T\) と回転角 \(\theta\) によって完全に特定されます。

剛体の重心に物体基準枠の原点を取り、剛体の質量を \(m\)、慣性モーメントを \(J\)、剛体に働く合力を \(\mathbf{F}\)、剛体に働く重心周りのトルクの和を \(M\) とすれば、剛体の運動方程式は次のニュートン・オイラー方程式で与えられます。

$$ \begin{cases} m\ddot{\mathbf{R}} = \mathbf{F} \\ J\ddot{\theta} = M \end{cases} \tag{1}$$

一方、可変形体とは剛体でない物体のことです。可変形体の配置を特定するには物体中のすべての点の位置を特定する必要があり、一般に無限個の座標が必要です。

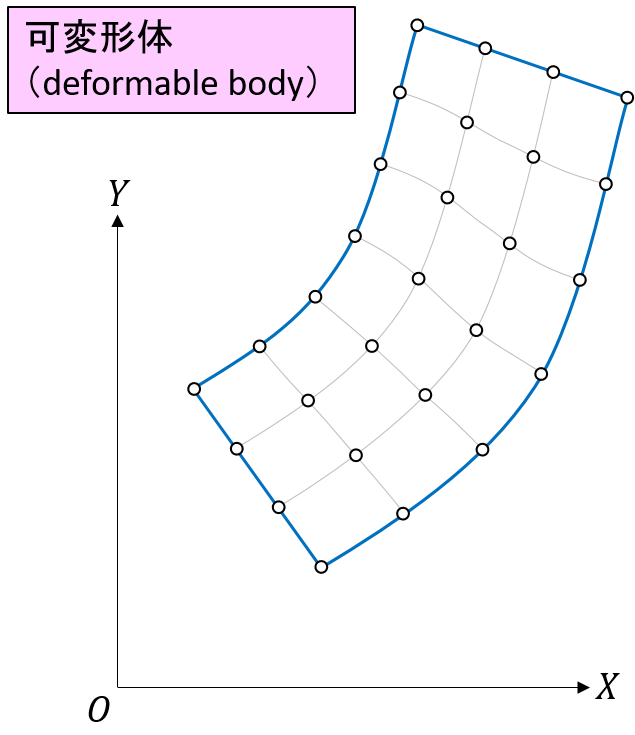
しかし、数値計算で無限個の座標を扱うことはできないので、マルチボディダイナミクスで可変形体を扱う場合には、何らかの近似法を用いて有限個の座標で可変形体の配置を表す必要があります。

浮動基準枠法とは

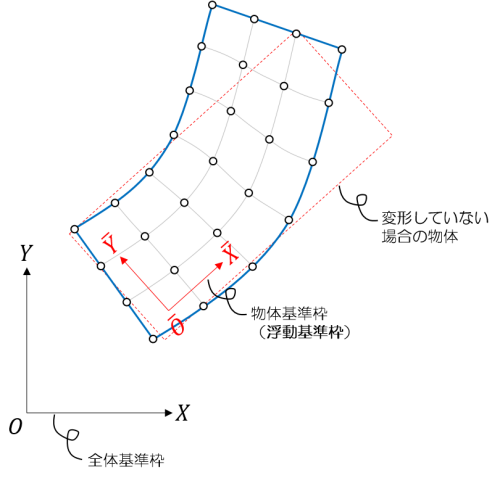
浮動基準枠法（Floating Frame of Reference Formulation / FFRF）とは、各可変形体に対して変形の基準となる物体基準枠（浮動基準枠）を定義し、各可変形体の配置を「物体基準枠の位置と回転姿勢」と「物体基準枠に対する物体の変形」の和として表すことによって、各可変形体の運動を記述する方法です。

変形の近似表現

浮動基準枠法において物体の変形をどのように近似するのか、下図のような一次元の可変形体の変形を例に説明します。

図中の座標軸は物体基準枠であるとします。物体の変形は、物体中の各点の物体基準枠に対する変位 \(u\) で定量化することができます。

変位 \(u\) は空間 \(x\) と時間 \(t\) の関数です。

$$ u=f(x,t) \tag{1}$$

しかし、空間 \(x\) は連続なので、式(1)を用いる場合、無限個の座標を扱わなくてはなりません。そこで \(N\) を有限な自然数として次のような近似を行います。

$$ u\approx\phi_1(x)q_1(t)+\phi_2(x)q_2(t)+\cdots+\phi_N(x)q_N(t) \tag{2}$$

ここで、\(\phi_1(x), \phi_2(x), \ldots, \phi_N(x)\) は空間 \(x\) のみに依存する形状関数と呼ばれるもの、\(q_1(t), q_2(t), \dots, q_N(t)\) は時間のみに依存する変形座標です。つまり、ある時点の変位場 \(u\) を有限個の形状関数の線形結合で表し、その結合係数をその時点の変形座標とするのです。これで可変形体の変形を有限個の座標で表すことができるようになります。

形状関数は自由に選ぶことができますが、想定する状況下で起こりうるすべての変形をできるだけ少ない変形座標で十分に近似できるように、注意深く選ぶ必要があります。与えられた形状関数の線形結合で表現可能な変位場は想定変位場と呼ばれます。

式(2) は次のような行列形式で書くこともできます。

$$ u = \mathbf{S}(x)\mathbf{q}_f(t), \tag{3} $$

$$
\mathbf{S}:=
\begin{bmatrix}
\phi_1(x) & \phi_2(x) & \cdots & \phi_N(x)
\end{bmatrix}, \quad
\mathbf{q}_f(t):=
\begin{bmatrix}
q_1(t) \\ q_2(t) \\ \vdots \\ q_N(t)
\end{bmatrix}
$$

ここで、\(\mathbf{S}\) は形状行列、\(\mathbf{q}_f\) は変形座標ベクトルと呼ばれます。

（例）弦の変形

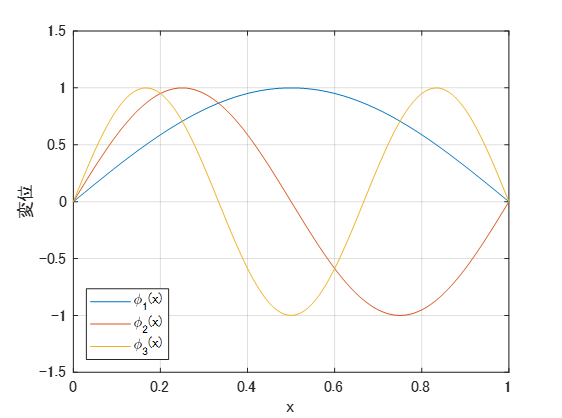
弦の変形を、有限個の定常波の重ね合わせで近似します。１次から３次までの定常波波形を形状関数として用いれば、弦の変形は次のように表せます。

$$ u(x,t) = \phi_1(x)q_1(t)+\phi_2(x)q_2(t)+\phi_3(x)q_3(t), $$

$$ \phi_i(x) = \sin\left(\frac{i\pi x}{l}\right), \quad i = 1, 2, 3 $$

ここで、\(l\) は弦の長さです。\(l=1\) の時の３つの形状関数を下図に示します。

仮に、変形座標を \( \begin{bmatrix}q_1 & q_2 & q_3\end{bmatrix}^T = \begin{bmatrix}0.2 & 0.4 & 0.4\end{bmatrix}^T \) とすれば、変位場は下図のようになります。

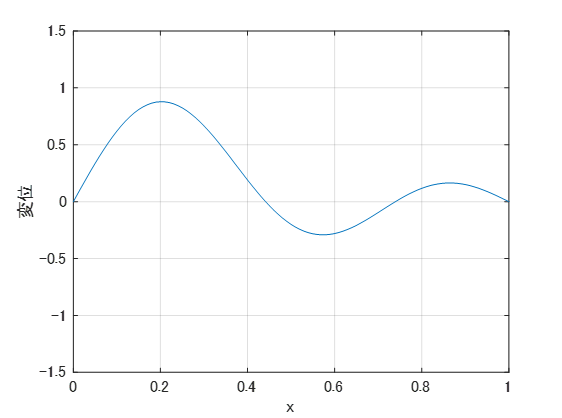
（例）はりの変形

はり（梁）とは、細長く、真っ直ぐな構造部材のことです。

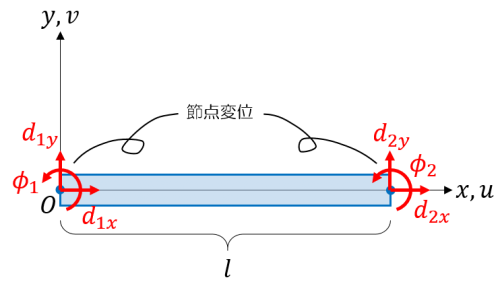
はりの変形については、軸方向変位 \(u\) を１次の多項式、横方向変位 \(v\) を３次の多項式で近似することが多いようです。

$$
\begin{cases}
u(x) = a_1 x + a_0 \\
v(x) = b_3 x^3 + b_2 x^2 + b_1 x + b_0
\end{cases} \tag{4}
$$

この多項式の係数 \(a_0, a_1, b_0, b_1, b_2, b_3\) をそのまま変形座標とすることも考えられますが、通常は節点の変位 \(d_{1x}, d_{1y}, \phi_1, d_{2x}, d_{2y}, \phi_2\) を変形座標とする方が便利です。

節点変位の定義

$$u(0)=d_{1x}, \quad v(0)=d_{1y}, \quad \frac{dv(0)}{dx}=\phi_1, $$

$$u(l)=d_{2x}, \quad v(l)=d_{2y}, \quad \frac{dv(l)}{dx}=\phi_2 $$

を用いれば、式(4)より

$$
\begin{bmatrix}
u \\ v
\end{bmatrix}
=
\underbrace{
\begin{bmatrix}
1-\xi & 0 & 0 & \xi & 0 & 0 \\
0 & 1-3\xi^2+2\xi^3 & l(\xi-2\xi^2+\xi^3) & 0 & 3\xi^2-2\xi^3 & l(\xi^3-\xi^2)
\end{bmatrix}
}_{\mathbf{S}(x)}
\underbrace{
\begin{bmatrix}
d_{1x} \\ d_{1y} \\ \phi_1 \\ d_{2x} \\ d_{2y} \\ \phi_2
\end{bmatrix}
}_{\mathbf{q}_f(t)}, \tag{5}
$$

$$ \xi = \frac{x}{l} $$

が得られます。

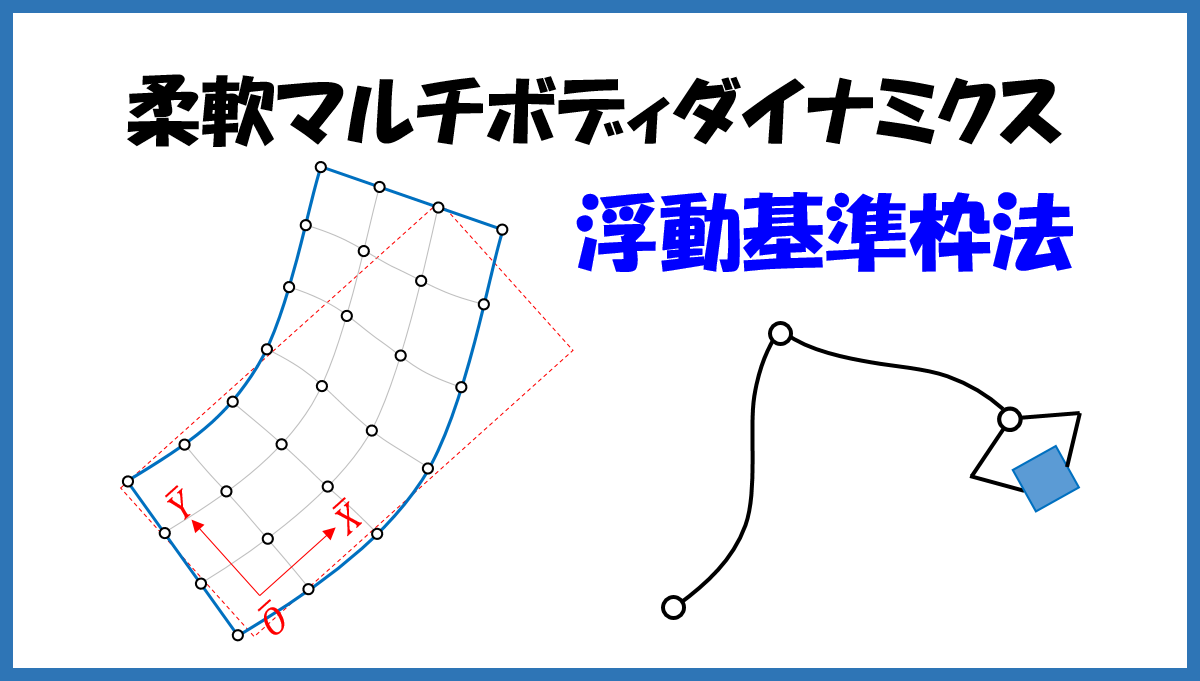
浮動基準枠と物体の位置座標

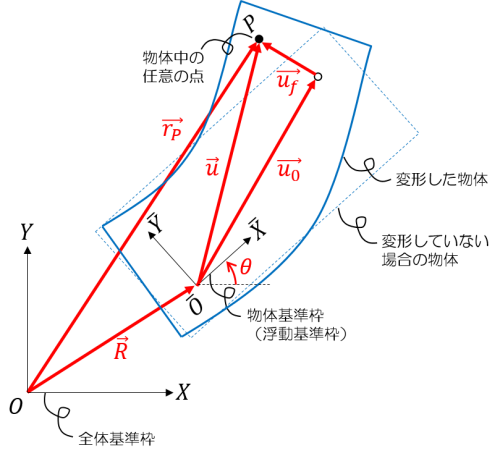
下図のような、一般の可変形物体の配置について考えます。

※以下では、位置ベクトル \(\vec{a}\) の全体基準枠による成分表示を \(\mathbf{a}\)、物体基準枠による成分表示を \(\bar{\mathbf{a}}\) と書きます。ベクトルの成分表示と座標変換については下の参考記事を参照してください。

物体中の任意の点 \(P\) の物体基準枠に対する位置 \(\vec{u}\) は、変形していない場合の \(P\) の位置 \(\vec{u_0}\) と変形による変位 \(\vec{u_f}\) を用いて

$$ \vec{u}=\vec{u_0}+\vec{u_f} \tag{6} $$

と表せます。\(\vec{u_0}, \vec{u_f}\)の物体基準枠による成分表示をそれぞれ \(\bar{\mathbf{u}}_0, \bar{\mathbf{u}}_f\)、物体の形状行列を \(\mathbf{S}(\bar{\mathbf{u}}_0)\)、変形座標ベクトルを \(\mathbf{q}_f\) とすれば、式(6)と(3)より \(\vec{u}\) の物体基準枠による成分表示は

$$ \bar{\mathbf{u}}=\bar{\mathbf{u}}_0+\bar{\mathbf{u}}_f=\bar{\mathbf{u}}_0+\mathbf{S}(\bar{\mathbf{u}}_0)\mathbf{q}_f \tag{7}$$

と表せます。物体基準枠の回転角を \(\theta\) とすると、物体基準枠の回転行列は

$$
\mathbf{A}:=
\begin{bmatrix}
\cos{\theta} & -\sin{\theta} \\
\sin{\theta} & \cos{\theta}
\end{bmatrix}
$$

で与えられ、\(\vec{u}\) の全体基準枠による成分表示は (7)を用いて

$$ \mathbf{u} = \mathbf{A}\bar{\mathbf{u}} = \mathbf{A}(\bar{\mathbf{u}}_0+\mathbf{S}(\bar{\mathbf{u}}_0)\mathbf{q}_f) \tag{8}$$

となります。物体基準枠の位置を \(\vec{R}\) とすると、点 \(P\) の全体基準枠に対する位置は

$$ \vec{r_P} = \vec{R}+\vec{u} \tag{9} $$

ですから、\(\vec{R}\) の全体基準枠による成分表示を \(\mathbf{R}\) とすれば、\(\vec{r_P}\) の全体基準枠による成分表示は(8)と(9)より

$$ \mathbf{r}_P = \mathbf{R} + \mathbf{u} = \mathbf{R} + \mathbf{A}(\bar{\mathbf{u}}_0+\mathbf{S}(\bar{\mathbf{u}}_0)\mathbf{q}_f) \tag{10}$$

となります。物体の一般化座標ベクトルを

$$
\mathbf{q}:=
\begin{bmatrix}
\mathbf{R} \\ \theta \\ \mathbf{q}_f
\end{bmatrix}
$$

とすれば、式(10)より、物体中の点の全体枠による位置座標 \(\mathbf{r}_P\) は \(\bar{\mathbf{u}}_0\) と \(\mathbf{q}\) の関数であることが分かります。

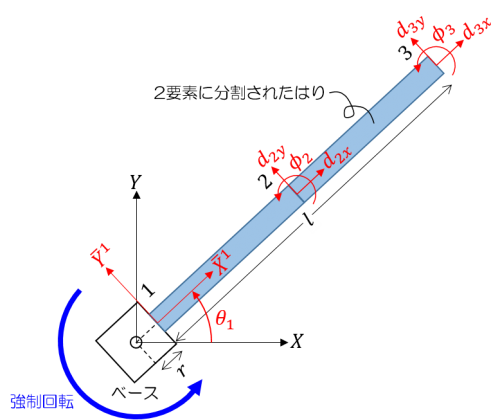
（例）１つのはり要素からなる物体の位置座標

１つのはり要素からなる物体を考えます。下図のように、物体基準枠は節点１に固定され、\(\bar{X}\) 軸は節点１ではりの接線方向と一致するように取るものとします。

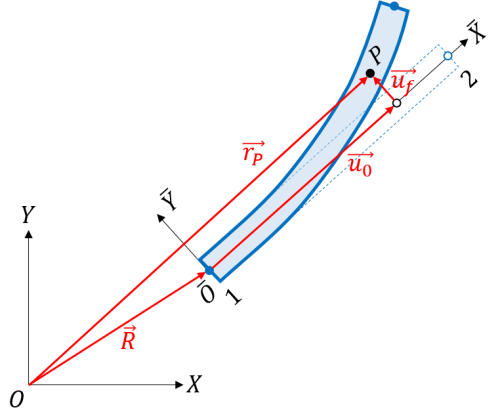
この場合、式(5)の節点１に関する変形座標はすべて０になるので、物体の変形座標としては節点２に関する変形座標だけが残ります。従って、この物体中の任意の点 \(P\) の全体基準枠による位置座標 \(\mathbf{r}_P\) は以下のように表せます。

$$ \mathbf{r}_P=\mathbf{R}+\mathbf{A}(\bar{\mathbf{u}}_0+\bar{\mathbf{u}}_f), $$

$$ \mathbf{R} = \begin{bmatrix} x \\ y \end{bmatrix}, \quad \mathbf{A}=
\begin{bmatrix}
\cos{\theta} & -\sin{\theta} \\
\sin{\theta} & \cos{\theta}
\end{bmatrix}
$$

$$
\bar{\mathbf{u}}_0 = \begin{bmatrix} \bar{x} \\ 0 \end{bmatrix}, \quad
\bar{\mathbf{u}}_f =
\underbrace{
\begin{bmatrix}
\xi & 0 & 0 \\
0 & 3\xi^2-2\xi^3 & l(\xi^3-\xi^2)
\end{bmatrix}
}_{\mathbf{S}(\bar{x})}
\underbrace{
\begin{bmatrix}
d_{2x} \\ d_{2y} \\ \phi_2
\end{bmatrix}
}_{\mathbf{q}_f(t)}, \quad
\xi = \frac{\bar{x}}{l}
$$

また、この物体の一般化座標ベクトルは

$$
\mathbf{q}=
\begin{bmatrix}
\mathbf{R} \\ \theta \\ \mathbf{q}_f
\end{bmatrix}
=
\begin{bmatrix}
x \\ y \\ \theta \\ d_{2x} \\ d_{2y} \\ \phi_2
\end{bmatrix}
$$

です。

可変形体の運動方程式

可変形体の運動方程式は、物体の運動エネルギー、弾性力、および外力を、式(10)を用いて一般化座標 \(\mathbf{q}\) および一般化速度 \(\dot{\mathbf{q}}\) の関数として求め、ラグランジュ方程式から導出できます。

浮動基準枠法による可変形体の運動方程式は一般に次式で与えられます。

$$ \mathbf{M}\ddot{\mathbf{q}} + \mathbf{K}\mathbf{q}=\mathbf{Q}_e+\mathbf{Q}_v $$

ここで、\(\mathbf{M}\) は質量行列で、物体の運動エネルギーを \(T\) とすると次式を満たします。

$$ T = \frac{1}{2}\dot{\mathbf{q}}^T\mathbf{M}\dot{\mathbf{q}} $$

また、\(\mathbf{K}\) は剛性行列で、物体の弾性エネルギーを \(U_f\) とすると次式を満たします。

$$ U_f = \frac{1}{2}\mathbf{q}^T\mathbf{K}\mathbf{q} $$

弾性エネルギーは変形座標 \(\mathbf{q}_f\) のみに依存し、基準座標 \(\mathbf{R}, \theta\) には依らないので、剛性行列は次のような形になります。

$$
\mathbf{K} =
\begin{bmatrix}
\mathbf{0} & \mathbf{0} & \mathbf{0} \\
\mathbf{0} & 0 & \mathbf{0} \\
\mathbf{0} & \mathbf{0} & \mathbf{K}_{ff}
\end{bmatrix}
$$

さらに、\(\mathbf{Q}_e\) は外力の一般化力ベクトル、また \(\mathbf{Q}_v\) は２次速度ベクトルで次式で与えられます。

$$ \mathbf{Q}_v = -\dot{\mathbf{M}}\dot{\mathbf{q}}+\frac{1}{2}\frac{\partial}{\partial\dot{\mathbf{q}}}(\dot{\mathbf{q}}^T\mathbf{M}\dot{\mathbf{q}}) $$

質量行列と２次速度ベクトルの具体的な表現およびはり要素の剛性行列を以下に示します。一般に、浮動基準枠法では剛性行列 \(\mathbf{K}\) が一定となりますが、質量行列 \(\mathbf{M}\) は \(\theta\) と \(\mathbf{q}_f\) に依存し、２次速度ベクトル \(\mathbf{Q}_v\) は \(\theta\) と \(\mathbf{q}_f\) およびそれらの時間微分に依存します。

質量行列

$$
\mathbf{M}=
\begin{bmatrix}
\mathbf{m}_{RR} & \mathbf{m}_{R\theta} & \mathbf{m}_{Rf} \\
& \mathbf{m}_{\theta\theta} & \mathbf{m}_{\theta f} \\
sym. & & \mathbf{m}_{ff}
\end{bmatrix}, \quad
\begin{cases}
\mathbf{m}_{RR} = m\mathbf{I} \\
\mathbf{m}_{R\theta} = \mathbf{A}_{\theta}\left[\mathbf{J}_u+\mathbf{J}_S\mathbf{q}_f\right] \\
\mathbf{m}_{Rf} = \mathbf{A}\mathbf{J}_S \\
\mathbf{m}_{\theta\theta} = \mathbf{J}_{uu}+2\mathbf{J}_{uS}\mathbf{q}_f+\mathbf{q}_f^T\mathbf{J}_{SS}\mathbf{q}_f \\
\mathbf{m}_{\theta f} = \mathbf{J}_{u\tilde{S}}+\mathbf{q}_f^T\mathbf{J}_{S\tilde{S}} \\
\mathbf{m}_{ff} = \mathbf{J}_{SS}
\end{cases},
$$

$$
\mathbf{I} = \begin{bmatrix}1 & 0 \\ 0 & 1\end{bmatrix}, \quad
\mathbf{A} = \begin{bmatrix}\cos{\theta} & -\sin{\theta} \\ \sin{\theta} & \cos{\theta}\end{bmatrix}, \quad
\mathbf{A}_{\theta} = \frac{\partial\mathbf{A}}{\partial\theta}= \begin{bmatrix}-\sin{\theta} & -\cos{\theta} \\ \cos{\theta} & -\sin{\theta}\end{bmatrix},
$$

$$
\begin{cases}
m = \int \rho \,dV \\
\mathbf{J}_u = \int \rho\bar{\mathbf{u}}_0 \,dV \\
\mathbf{J}_S = \int \rho \mathbf{S} \,dV \\
\mathbf{J}_{uu} = \int \rho\bar{\mathbf{u}}_0^T\bar{\mathbf{u}}_0 \,dV \\
\mathbf{J}_{uS} = \int \rho\bar{\mathbf{u}}_0^T\mathbf{S} \,dV \\
\mathbf{J}_{SS} = \int \rho\mathbf{S}^T\mathbf{S} \,dV \\
\mathbf{J}_{u\tilde{S}} = \int \rho\bar{\mathbf{u}}_0^T\tilde{\mathbf{I}}\mathbf{S} \,dV \\
\mathbf{J}_{S\tilde{S}} = \int \rho\mathbf{S}^T\tilde{\mathbf{I}}\mathbf{S} \,dV
\end{cases},
$$

$$
\tilde{\mathbf{I}} = \mathbf{A}_\theta^T\mathbf{A} = \begin{bmatrix}0 & 1 \\ -1 & 0\end{bmatrix}
$$

（\(\rho\) は物体の質量密度）

２次速度ベクトル

$$
\mathbf{Q}_v =
\begin{bmatrix}
\dot{\theta}^2\mathbf{A}\left(\mathbf{J}_u+\mathbf{J}_S\mathbf{q}_f\right)-2\dot{\theta}\mathbf{A}_{\theta}\mathbf{J}_S\dot{\mathbf{q}}_f \\
-2\dot{\theta}\left(\mathbf{J}_{uS}+\mathbf{q}_f^T\mathbf{J}_{SS}\right)\dot{\mathbf{q}}_f \\
\dot{\theta}^2\left(\mathbf{J}_{uS}^T+\mathbf{J}_{SS}\mathbf{q}_f\right)+2\dot{\theta}\mathbf{J}_{S\tilde{S}}\dot{\mathbf{q}}_f
\end{bmatrix}
$$

はり要素の剛性行列

式(5)によるはり要素で、軸剛性を \(EA\)、曲げ剛性を \(EI\) とするとき：

$$
\mathbf{K}_{ff} =
\begin{bmatrix}
c_1 & 0 & 0 & -c_1 & 0 & 0 \\
& 12c_2 & 6c_2 l & 0 & -12c_2 & 6c_2 l \\
& & 4c_2 l^2 & 0 & -6c_2 l & 2c_2 l^2 \\
& & & c_1 & 0 & 0 \\
& sym. & & & 12c_2 & -6c_2 l \\
& & & & & 4c_2 l^2
\end{bmatrix}, \quad
c_1 = \frac{EA}{l}, \quad c_2 = \frac{EI}{l^3}
$$

柔軟マルチボディシステムの運動方程式

マルチボディシステムが \(n_b\) 個の可変形物体で構成されているとき、各物体の一般化座標ベクトルを \(\mathbf{q}^i, i=1,2,\ldots, n_b\) とすれば、マルチボディシステムの一般化座標ベクトルは

$$ \mathbf{q} := \begin{bmatrix} \mathbf{q}^1 \\ \mathbf{q}^2 \\ \vdots \\ \mathbf{q}^{n_b} \end{bmatrix} $$

と書けます。

物体間の各種ジョイントによる拘束は、\(n_c\) 個の位置拘束式

$$ C_j(\mathbf{q}, t) = 0, \quad j = 1, 2, \ldots, n_c $$

で与えられるものとし、全拘束式をまとめて

$$
\mathbf{C}(\mathbf{q}, t) :=
\begin{bmatrix} C_1(\mathbf{q}, t) \\ C_2(\mathbf{q}, t) \\ \vdots \\ C_{n_c}(\mathbf{q}, t) \end{bmatrix}
= \mathbf{0}
$$

と書きます。

位置拘束を含むマルチボディシステムの運動方程式は、次の微分代数方程式で与えられます。

$$
\begin{cases}
\mathbf{M}\ddot{\mathbf{q}}+\mathbf{K}\mathbf{q}+\mathbf{C}_{\mathbf{q}}^T\boldsymbol{\lambda} = \mathbf{Q}_e+\mathbf{Q}_v \\
\mathbf{C}(\mathbf{q}, t) = \mathbf{0}
\end{cases}\tag{11}
$$

ここで、

$$
\mathbf{M}:=
\begin{bmatrix}
\mathbf{M}^1 &  &  & \mathbf{0} \\
& \mathbf{M}^2 &  & \\
&  & \ddots & \\
\mathbf{0} &  &  & \mathbf{M}^{n_b}
\end{bmatrix}, \quad
\mathbf{K}:=
\begin{bmatrix}
\mathbf{K}^1 &  &  & \mathbf{0} \\
& \mathbf{K}^2 &  & \\
&  & \ddots & \\
\mathbf{0} &  &  & \mathbf{K}^{n_b}
\end{bmatrix},
$$

はそれぞれシステムの質量行列と剛性行列で、\(\mathbf{M}^i, \mathbf{K}^i\) はそれぞれ各物体の質量行列と剛性行列です。また、

$$
\mathbf{Q}_e:=\begin{bmatrix} \mathbf{Q}_e^1 \\ \mathbf{Q}_e^2 \\ \vdots \\ \mathbf{Q}_e^{n_b} \end{bmatrix}, \quad
\mathbf{Q}_v:=\begin{bmatrix} \mathbf{Q}_v^1 \\ \mathbf{Q}_v^2 \\ \vdots \\ \mathbf{Q}_v^{n_b} \end{bmatrix}
$$

はそれぞれシステムの外力ベクトルと２次速度ベクトルで、\(\mathbf{Q}_e^i, \mathbf{Q}_v^i\) はそれぞれ各物体に働く外力の一般化力（拘束力を除く）と各物体の２次速度ベクトルです。さらに、

$$
\mathbf{C}_{\mathbf{q}} :=
\begin{bmatrix} \mathbf{C}_{\mathbf{q}^1} & \mathbf{C}_{\mathbf{q}^2} & \cdots & \mathbf{C}_{\mathbf{q}^{n_b}} \end{bmatrix}, \quad
\mathbf{C}_{\mathbf{q}^i} := \frac{\partial\mathbf{C}}{\partial\mathbf{q}^i} =
\begin{bmatrix}
\frac{\partial C_1}{\partial \mathbf{R}^i} & \frac{\partial C_1}{\partial \theta^i} & \frac{\partial C_1}{\partial \mathbf{q}_f^i} \\
\frac{\partial C_2}{\partial \mathbf{R}^i} & \frac{\partial C_2}{\partial \theta^i} & \frac{\partial C_2}{\partial \mathbf{q}_f^i} \\
\vdots & \vdots & \vdots \\
\frac{\partial C_{n_c}}{\partial \mathbf{R}^i} & \frac{\partial C_{n_c}}{\partial \theta^i} & \frac{\partial C_{n_c}}{\partial \mathbf{q}_f^i}
\end{bmatrix}
$$

は拘束ヤコビアン、\(\boldsymbol{\lambda}:=\begin{bmatrix}\lambda_1&\lambda_2&\ldots&\lambda_{n_c}\end{bmatrix}^T\) はラグランジュの未定乗数で、項 \( \mathbf{C}_{\mathbf{q}}^T\boldsymbol{\lambda} \) が拘束力の一般化力に相当します。

式(11)は、\(\mathbf{Q} := \mathbf{Q}_e+\mathbf{Q}_v-\mathbf{K}\mathbf{q}\) と置けば 前回の「マルチボディダイナミクス超入門」で論じた剛体のみで構成されるマルチボディシステムの運動方程式と同じ形になり、基本的には同じ方法で動力学解析および静力学解析の数値計算を行うことができます。ただし、今回は質量行列 \(\mathbf{M}\) が変形座標に依存するので、変形に応じて質量行列を更新する必要があります。

解析例

可変形体を含むマルチボディシステムの浮動基準枠法による動解析例を３つ示します。いずれもはり要素を含む簡単なマルチボディシステムです。

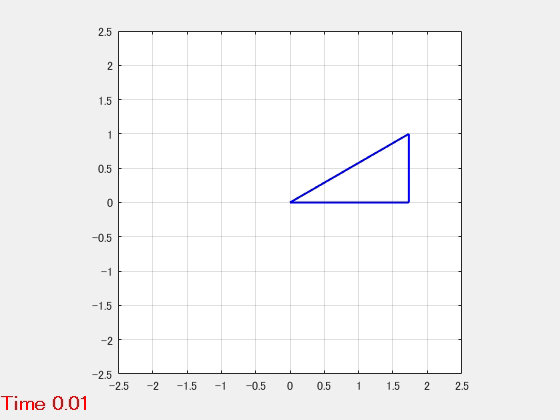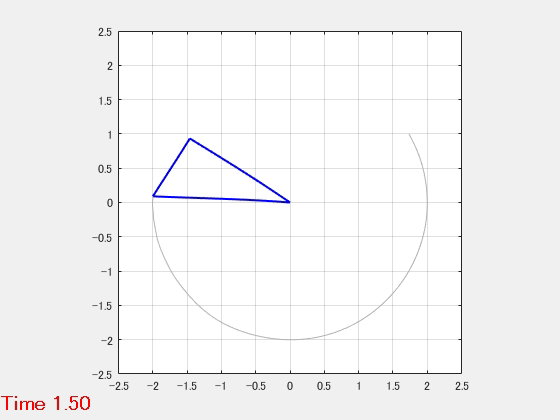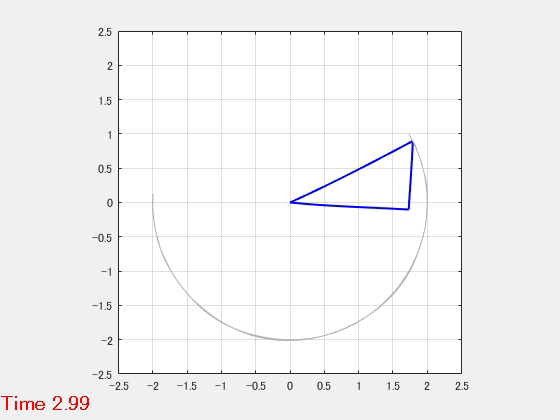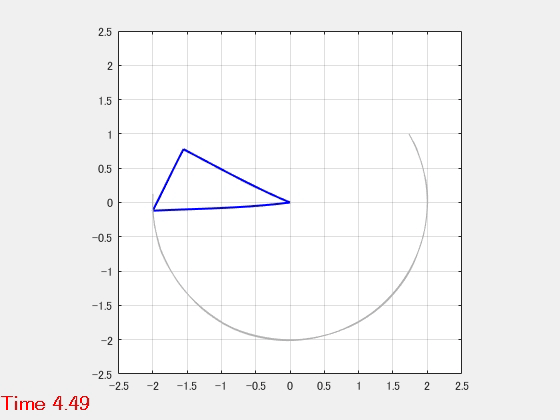
L字型振子

はりと剛体棒からなるL字型振子のモデルです。

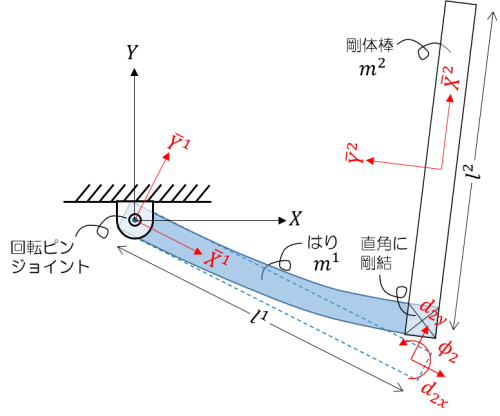
• パラメータ

• 動解析結果のアニメーション

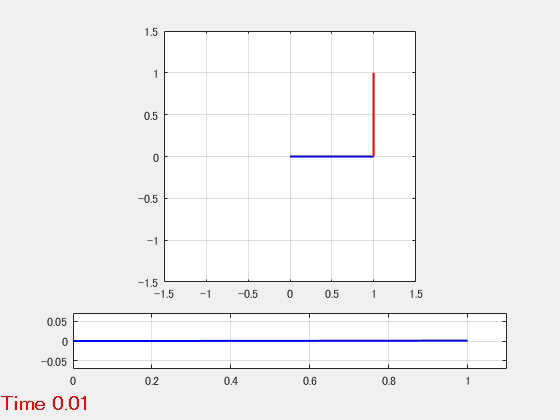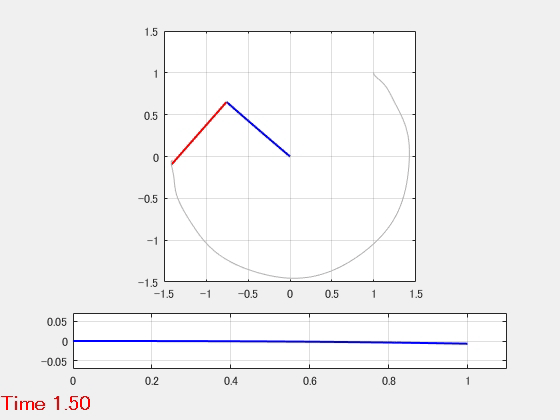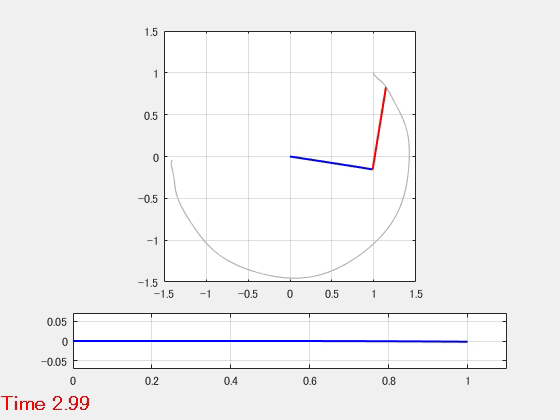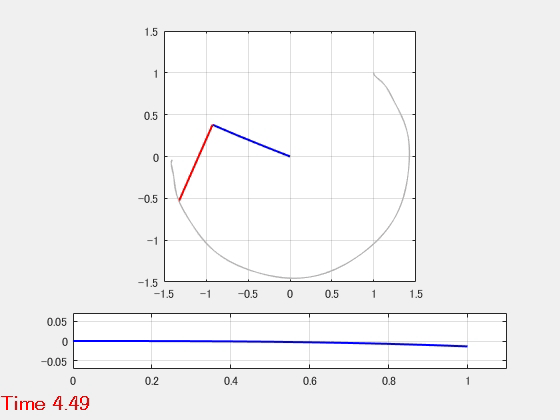
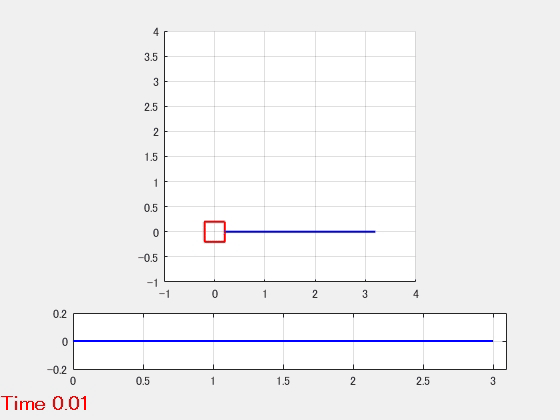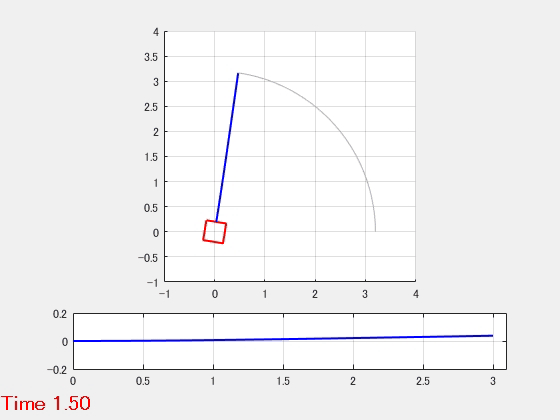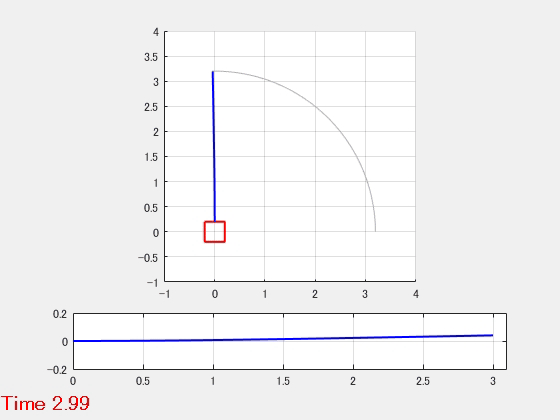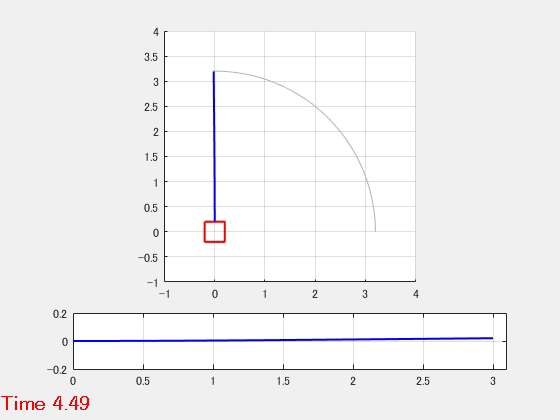
柔軟アーム

２つのはり要素からなるアームを強制回転するモデルです。

• パラメータ

• 強制回転入力

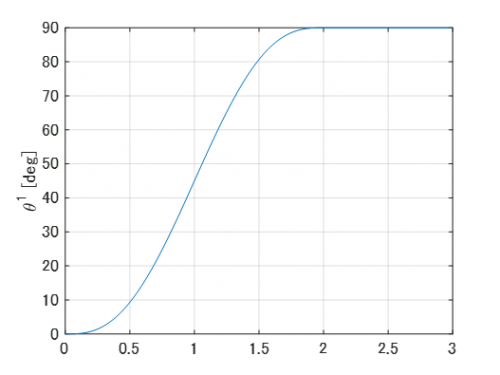
• 動解析結果のアニメーション

三角フレーム振子

三つのはり要素から構成される三角フレームの一端を回転ピンで固定した振子のモデルです。

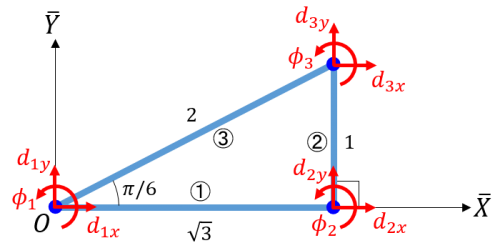
• パラメータ（弾性変形が分かりやすいように、剛性を柔らかめに設定しています。）

• 動解析結果のアニメーション

まとめ

この記事では、可変形体を含むマルチボディシステムの浮動基準枠法による解法を紹介しました。浮動基準枠法では、可変形体の運動を「物体基準枠の並進・回転運動」と「物体基準枠に対する物体の変形」の和として表します。可変形体の変形は有限個の形状関数の線形結合で近似し、結合係数を変形座標として扱います。可変形体の運動方程式はラグランジュ方程式から導出でき、質量行列、剛性行列、外力ベクトル、２次速度ベクトルで構成されます。質量行列と２次速度ベクトルは物体の変形座標に依存します。可変形体を含むマルチボディシステムの運動方程式は、個々の物体の運動方程式と拘束式から構成される微分代数方程式になり、基本的には剛体のみで構成されるマルチボディシステムの場合と同じ方法で動力学解析および静力学解析の数値計算を行うことができます。

参考文献

[1] Shabana, A. A. Dynamics of Multibody Systems. 4th edition, Cambridge, 2013.