運動する2つの点の相対速度は「どの座標系から見るか」に依ります。絶対座標系に対して回転運動していない座標系から見た場合には、相対速度は単に絶対速度の差と等しくなりますが、回転運動している座標系から見た場合には、一般に相対速度は絶対速度の差とは異なるので注意が必要です。この記事では、回転する座標系から見た相対速度や相対加速度を正しく計算する方法について解説します。
予備知識
以下の解説では、ベクトルの成分表示と座標変換、回転行列、角速度ベクトルと回転行列の時間微分を利用しています。これらの概念については、関連記事で詳しく解説していますので、必要に応じて参照してください。
全体基準枠と移動枠 \(I, J, K, L\)
下図のように、全体基準枠と4つの移動枠 \(I, J, K, L\) を考えます。枠 \(I\) と枠 \(J\) を観測対象、枠 \(L\) を観測基準枠、枠 \(K\) をベクトル成分表示の参照枠とします。
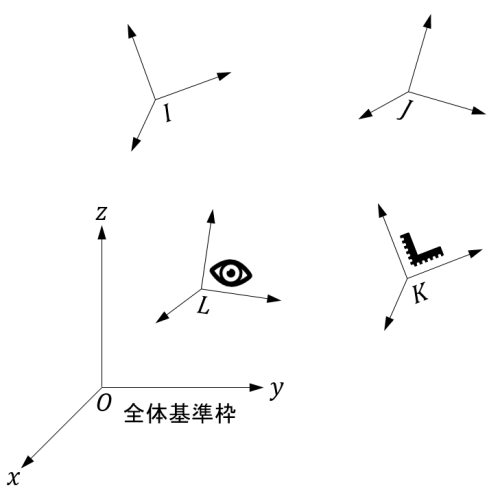
全体基準枠に対する、移動枠 \(X\)(\(X\in\{I, J, K, L\}\))の位置ベクトルと角速度ベクトルの全体基準枠による成分表示をそれぞれ \(\mathbf{r}_X\) と \(\boldsymbol{\omega}_X\)、回転行列を \(\mathbf{R}_X\) と書きます。全体基準枠に対する各枠の位置ベクトル \(\mathbf{r}_X\)、回転行列 \(\mathbf{R}_X\)、速度ベクトル \(\dot{\mathbf{r}}_X\)、角速度ベクトル \(\boldsymbol{\omega}_X\)、加速度ベクトル \(\ddot{\mathbf{r}}_X\)、角加速度ベクトル \(\dot{\boldsymbol{\omega}}_X\) は既知であるとします。
観測枠 \(L\) を介した枠 \(I\) と枠 \(J\) の位置・速度・加速度の表現
枠 \(L\) に対する枠 \(I\) の位置ベクトルの枠 \(K\) による成分表示を \(\mathbf{r}_{LI}^{(K)}\) と書くこととします。
枠 \(I\) の位置ベクトルに関して次式が成り立ちます。
$$ \mathbf{r}_I = \mathbf{r}_L + \mathbf{R}_L\mathbf{r}_{LI}^{(L)} \tag{1} $$
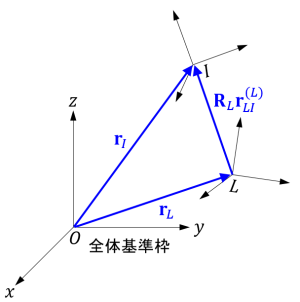
式(1)を時間微分し、回転行列の時間微分と角速度ベクトルの関係
$$\dot{\mathbf{R}}_L=\widetilde{\boldsymbol{\omega}}_L\mathbf{R}_L \tag{2}$$
を用いれば、枠 \(I\) の速度ベクトルに関する次式が得られます。
$$
\begin{align}
\dot{\mathbf{r}}_I
& =
\dot{\mathbf{r}}_L
+\dot{\mathbf{R}}_L\mathbf{r}_{LI}^{(L)}
+\mathbf{R}_L\dot{\mathbf{r}}_{LI}^{(L)} \\
& =
\dot{\mathbf{r}}_L
+\widetilde{\boldsymbol{\omega}}_L\mathbf{R}_L\mathbf{r}_{LI}^{(L)}
+\mathbf{R}_L\dot{\mathbf{r}}_{LI}^{(L)} \tag{3}
\end{align}
$$
式(3)をさらに時間微分し、式(2)を再度用いれば、枠 \(I\) の加速度ベクトルに関する次式が得られます。
$$
\begin{align}
\ddot{\mathbf{r}}_I
& =
\ddot{\mathbf{r}}_L
+\widetilde{\dot{\boldsymbol{\omega}}}_L\mathbf{R}_L\mathbf{r}_{LI}^{(L)}
+\widetilde{\boldsymbol{\omega}}_L\dot{\mathbf{R}}_L\mathbf{r}_{LI}^{(L)}
+\widetilde{\boldsymbol{\omega}}_L\mathbf{R}_L\dot{\mathbf{r}}_{LI}^{(L)}
+\dot{\mathbf{R}}_L\dot{\mathbf{r}}_{LI}^{(L)}
+\mathbf{R}_L\ddot{\mathbf{r}}_{LI}^{(L)} \\
& =
\ddot{\mathbf{r}}_L
+\left(\widetilde{\dot{\boldsymbol{\omega}}}_L+\widetilde{\boldsymbol{\omega}}_L\widetilde{\boldsymbol{\omega}}_L\right)\mathbf{R}_L\mathbf{r}_{LI}^{(L)}
+2\widetilde{\boldsymbol{\omega}}_L\mathbf{R}_L\dot{\mathbf{r}}_{LI}^{(L)}
+\mathbf{R}_L\ddot{\mathbf{r}}_{LI}^{(L)} \tag{4}
\end{align}
$$
同様に、枠 \(J\) の位置ベクトル、速度ベクトル、加速度ベクトルに関して以下の式が成り立ちます。
$$ \mathbf{r}_J = \mathbf{r}_L + \mathbf{R}_L\mathbf{r}_{LJ}^{(L)} \tag{5} $$
$$
\dot{\mathbf{r}}_J =
\dot{\mathbf{r}}_L
+\widetilde{\boldsymbol{\omega}}_L\mathbf{R}_L\mathbf{r}_{LJ}^{(L)}
+\mathbf{R}_L\dot{\mathbf{r}}_{LJ}^{(L)} \tag{6}
$$
$$
\ddot{\mathbf{r}}_J =
\ddot{\mathbf{r}}_L
+\left(\widetilde{\dot{\boldsymbol{\omega}}}_L+\widetilde{\boldsymbol{\omega}}_L\widetilde{\boldsymbol{\omega}}_L\right)\mathbf{R}_L\mathbf{r}_{LJ}^{(L)}
+2\widetilde{\boldsymbol{\omega}}_L\mathbf{R}_L\dot{\mathbf{r}}_{LJ}^{(L)}
+\mathbf{R}_L\ddot{\mathbf{r}}_{LJ}^{(L)} \tag{7}
$$
観測枠 \(L\) を介した枠 \(I\) と枠 \(J\) の角速度・角加速度の表現
枠 \(L\) に対する枠 \(I\) の角速度ベクトルの枠 \(K\) による成分表示を \(\boldsymbol{\omega}_{LI}^{(K)}\) と書くこととします。
枠 \(I\) の角速度ベクトルに関して次式が成り立ちます。
$$\boldsymbol{\omega}_I = \boldsymbol{\omega}_L + \mathbf{R}_L\boldsymbol{\omega}_{LI}^{(L)} \tag{8}$$
式(8)を時間微分し、式(2)を用いれば、枠 \(I\) の角加速度ベクトルに関する次式が得られます。
$$
\begin{align}
\dot{\boldsymbol{\omega}}_I
& =
\dot{\boldsymbol{\omega}}_L
+ \dot{\mathbf{R}}_L\boldsymbol{\omega}_{LI}^{(L)}
+ \mathbf{R}_L\dot{\boldsymbol{\omega}}_{LI}^{(L)} \\
& =
\dot{\boldsymbol{\omega}}_L
+ \widetilde{\boldsymbol{\omega}}_L\mathbf{R}_L\boldsymbol{\omega}_{LI}^{(L)}
+ \mathbf{R}_L\dot{\boldsymbol{\omega}}_{LI}^{(L)} \tag{9}
\end{align}
$$
同様に、枠 \(J\) の角速度ベクトル、角加速度ベクトルに関して以下の式が成り立ちます。
$$\boldsymbol{\omega}_J = \boldsymbol{\omega}_L + \mathbf{R}_L\boldsymbol{\omega}_{LJ}^{(L)} \tag{10}$$
$$
\dot{\boldsymbol{\omega}}_J =
\dot{\boldsymbol{\omega}}_L
+ \widetilde{\boldsymbol{\omega}}_L\mathbf{R}_L\boldsymbol{\omega}_{LJ}^{(L)}
+ \mathbf{R}_L\dot{\boldsymbol{\omega}}_{LJ}^{(L)} \tag{11}
$$
相対位置ベクトル
枠 \(L\) から見た、枠 \(J\) に対する枠 \(I\) の相対位置ベクトルの枠 \(L\) による成分表示は、次のように定義されます。
$$ \mathbf{r}_{L\to JI}^{(L)} \equiv \mathbf{r}_{LI}^{(L)}-\mathbf{r}_{LJ}^{(L)} \tag{12} $$
式(1)から式(5)を引いて
$$ \mathbf{r}_I-\mathbf{r}_J = \mathbf{R}_L\left(\mathbf{r}_{LI}^{(L)}-\mathbf{r}_{LJ}^{(L)}\right) $$
式(12)を代入すると
$$ \mathbf{r}_I-\mathbf{r}_J = \mathbf{R}_L\mathbf{r}_{L\to JI}^{(L)} $$
この式を \(\mathbf{r}_{L\to JI}^{(L)}\) について解けば、
$$ \mathbf{r}_{L\to JI}^{(L)} = (\mathbf{R}_L)^T(\mathbf{r}_I-\mathbf{r}_J) \tag{13}$$
を得ます。式(13)を座標変換して枠 \(K\) による成分表示を求めれば次のようになります。
$$ \mathbf{r}_{L\to JI}^{(K)} = (\mathbf{R}_K)^T(\mathbf{r}_I-\mathbf{r}_J) $$
相対位置ベクトルは、観測枠 \(L\) に依りません。
相対速度ベクトル
枠 \(L\) から見た、枠 \(J\) に対する枠 \(I\) の相対速度ベクトルの枠 \(L\) による成分表示は、次のように定義されます。
$$ \mathbf{v}_{L\to JI}^{(L)} \equiv \dot{\mathbf{r}}_{LI}^{(L)}-\dot{\mathbf{r}}_{LJ}^{(L)} \tag{14} $$
式(3)から式(6)を引いて
$$
\dot{\mathbf{r}}_I-\dot{\mathbf{r}}_J =
\widetilde{\boldsymbol{\omega}}_L\mathbf{R}_L\left(\mathbf{r}_{LI}^{(L)}-\mathbf{r}_{LJ}^{(L)}\right)
+\mathbf{R}_L\left(\dot{\mathbf{r}}_{LI}^{(L)}-\dot{\mathbf{r}}_{LJ}^{(L)}\right)
$$
式(12)(14)を代入すると
$$
\dot{\mathbf{r}}_I-\dot{\mathbf{r}}_J =
\widetilde{\boldsymbol{\omega}}_L\mathbf{R}_L\mathbf{r}_{L\to JI}^{(L)}
+\mathbf{R}_L\mathbf{v}_{L\to JI}^{(L)}
$$
この式を \(\mathbf{v}_{L\to JI}^{(L)}\) について解き、式(13)を代入すれば、
$$
\begin{align}
\mathbf{v}_{L\to JI}^{(L)}
& =
(\mathbf{R}_L)^T \left\{
(\dot{\mathbf{r}}_I-\dot{\mathbf{r}}_J)
-\widetilde{\boldsymbol{\omega}}_L\mathbf{R}_L\mathbf{r}_{L\to JI}^{(L)}\right\} \\
& =
(\mathbf{R}_L)^T \left\{
(\dot{\mathbf{r}}_I-\dot{\mathbf{r}}_J)
-\widetilde{\boldsymbol{\omega}}_L(\mathbf{r}_I-\mathbf{r}_J)\right\} \tag{15}
\end{align}
$$
を得ます。式(15)を座標変換して枠 \(K\) による成分表示を求めれば次のようになります。
$$
\mathbf{v}_{L\to JI}^{(K)} =
(\mathbf{R}_K)^T \left\{
(\dot{\mathbf{r}}_I-\dot{\mathbf{r}}_J)
-\widetilde{\boldsymbol{\omega}}_L(\mathbf{r}_I-\mathbf{r}_J)\right\}
$$
相対加速度ベクトル
枠 \(L\) から見た、枠 \(J\) に対する枠 \(I\) の相対加速度ベクトルの枠 \(L\) による成分表示は、次のように定義されます。
$$ \mathbf{a}_{L\to JI}^{(L)} \equiv \ddot{\mathbf{r}}_{LI}^{(L)}-\ddot{\mathbf{r}}_{LJ}^{(L)} \tag{16} $$
式(4)から式(7)を引いて
$$
\ddot{\mathbf{r}}_I-\ddot{\mathbf{r}}_J =
\left(\widetilde{\dot{\boldsymbol{\omega}}}_L+\widetilde{\boldsymbol{\omega}}_L\widetilde{\boldsymbol{\omega}}_L\right)\mathbf{R}_L\left(\mathbf{r}_{LI}^{(L)}-\mathbf{r}_{LJ}^{(L)}\right)
+2\widetilde{\boldsymbol{\omega}}_L\mathbf{R}_L\left(\dot{\mathbf{r}}_{LI}^{(L)}-\dot{\mathbf{r}}_{LJ}^{(L)}\right)
+\mathbf{R}_L\left(\ddot{\mathbf{r}}_{LI}^{(L)}-\ddot{\mathbf{r}}_{LJ}^{(L)}\right)
$$
式(12)(14)(16)を代入すると
$$
\ddot{\mathbf{r}}_I-\ddot{\mathbf{r}}_J =
\left(\widetilde{\dot{\boldsymbol{\omega}}}_L+\widetilde{\boldsymbol{\omega}}_L\widetilde{\boldsymbol{\omega}}_L\right)\mathbf{R}_L\mathbf{r}_{L\to JI}^{(L)}
+2\widetilde{\boldsymbol{\omega}}_L\mathbf{R}_L\mathbf{v}_{L\to JI}^{(L)}
+\mathbf{R}_L\mathbf{a}_{L\to JI}^{(L)}
$$
この式を \(\mathbf{a}_{L\to JI}^{(L)}\) について解き、式(13)(15)を代入すれば、
$$
\begin{align}
\mathbf{a}_{L\to JI}^{(L)}
& =
(\mathbf{R}_L)^T
\left\{
(\ddot{\mathbf{r}}_I-\ddot{\mathbf{r}}_J)
-\left(\widetilde{\dot{\boldsymbol{\omega}}}_L+\widetilde{\boldsymbol{\omega}}_L\widetilde{\boldsymbol{\omega}}_L\right)\mathbf{R}_L\mathbf{r}_{L\to JI}^{(L)}
-2\widetilde{\boldsymbol{\omega}}_L\mathbf{R}_L\mathbf{v}_{L\to JI}^{(L)}
\right\} \\
& =
(\mathbf{R}_L)^T
\left\{
(\ddot{\mathbf{r}}_I-\ddot{\mathbf{r}}_J)
-\left(\widetilde{\dot{\boldsymbol{\omega}}}_L-\widetilde{\boldsymbol{\omega}}_L\widetilde{\boldsymbol{\omega}}_L\right)(\mathbf{r}_I-\mathbf{r}_J)
-2\widetilde{\boldsymbol{\omega}}_L(\dot{\mathbf{r}}_I-\dot{\mathbf{r}}_J)
\right\} \tag{17}
\end{align}
$$
を得ます。式(17)を座標変換して枠 \(K\) による成分表示を求めれば次のようになります。
$$
\mathbf{a}_{L\to JI}^{(K)} =
(\mathbf{R}_K)^T
\left\{
(\ddot{\mathbf{r}}_I-\ddot{\mathbf{r}}_J)
-\left(\widetilde{\dot{\boldsymbol{\omega}}}_L-\widetilde{\boldsymbol{\omega}}_L\widetilde{\boldsymbol{\omega}}_L\right)(\mathbf{r}_I-\mathbf{r}_J)
-2\widetilde{\boldsymbol{\omega}}_L(\dot{\mathbf{r}}_I-\dot{\mathbf{r}}_J)
\right\}
$$
相対角速度ベクトル
枠 \(L\) から見た、枠 \(J\) に対する枠 \(I\) の相対角速度ベクトルの枠 \(L\) による成分表示は、次のように定義されます。
$$ \boldsymbol{\omega}_{L\to JI}^{(L)} \equiv \boldsymbol{\omega}_{LI}^{(L)}-\boldsymbol{\omega}_{LJ}^{(L)} \tag{18}$$
式(8)から式(10)を引いて
$$
\boldsymbol{\omega}_I-\boldsymbol{\omega}_J =
\mathbf{R}_L\left(\boldsymbol{\omega}_{LI}^{(L)}-\boldsymbol{\omega}_{LJ}^{(L)}\right)
$$
式(18)を代入すると
$$
\boldsymbol{\omega}_I-\boldsymbol{\omega}_J =
\mathbf{R}_L\boldsymbol{\omega}_{L\to JI}^{(L)}
$$
この式を \(\boldsymbol{\omega}_{L\to JI}^{(L)}\) について解けば
$$
\boldsymbol{\omega}_{L\to JI}^{(L)} =
(\mathbf{R}_L)^T(\boldsymbol{\omega}_I-\boldsymbol{\omega}_J) \tag{19}
$$
を得ます。式(19)を座標変換して枠 \(K\) による成分表示を求めれば次のようになります。
$$
\boldsymbol{\omega}_{L\to JI}^{(K)} =
(\mathbf{R}_K)^T(\boldsymbol{\omega}_I-\boldsymbol{\omega}_J)
$$
相対角速度ベクトルは、観測枠 \(L\) に依りません。
相対角加速度ベクトル
枠 \(L\) から見た、枠 \(J\) に対する枠 \(I\) の相対角加速度ベクトルの枠 \(L\) による成分表示は、次のように定義されます。
$$ \boldsymbol{\alpha}_{L\to JI}^{(L)} \equiv \dot{\boldsymbol{\omega}}_{LI}^{(L)}-\dot{\boldsymbol{\omega}}_{LJ}^{(L)} \tag{20} $$
式(9)から式(11)を引いて
$$
\dot{\boldsymbol{\omega}}_I-\dot{\boldsymbol{\omega}}_J =
\widetilde{\boldsymbol{\omega}}_L\mathbf{R}_L\left(\boldsymbol{\omega}_{LI}^{(L)}-\boldsymbol{\omega}_{LJ}^{(L)}\right)
+ \mathbf{R}_L\left(\dot{\boldsymbol{\omega}}_{LI}^{(L)}-\dot{\boldsymbol{\omega}}_{LJ}^{(L)}\right)
$$
式(18)(20)を代入すると
$$
\dot{\boldsymbol{\omega}}_I-\dot{\boldsymbol{\omega}}_J =
\widetilde{\boldsymbol{\omega}}_L\mathbf{R}_L\boldsymbol{\omega}_{L\to JI}^{(L)}
+ \mathbf{R}_L\boldsymbol{\alpha}_{L\to JI}^{(L)}
$$
この式を \(\boldsymbol{\alpha}_{L\to JI}^{(L)}\) について解き、式(19)を代入すれば
$$
\begin{align}
\boldsymbol{\alpha}_{L\to JI}^{(L)}
& =
(\mathbf{R}_L)^T
\left\{
(\dot{\boldsymbol{\omega}}_I-\dot{\boldsymbol{\omega}}_J)
-\widetilde{\boldsymbol{\omega}}_L\mathbf{R}_L\boldsymbol{\omega}_{L\to JI}^{(L)}
\right\} \\
& =
(\mathbf{R}_L)^T
\left\{
(\dot{\boldsymbol{\omega}}_I-\dot{\boldsymbol{\omega}}_J)
-\widetilde{\boldsymbol{\omega}}_L(\boldsymbol{\omega}_I-\boldsymbol{\omega}_J)
\right\} \tag{21}
\end{align}
$$
を得ます。式(21)を座標変換して枠 \(K\) による成分表示を求めれば次のようになります。
$$
\boldsymbol{\alpha}_{L\to JI}^{(K)} =
(\mathbf{R}_K)^T
\left\{
(\dot{\boldsymbol{\omega}}_I-\dot{\boldsymbol{\omega}}_J)
-\widetilde{\boldsymbol{\omega}}_L(\boldsymbol{\omega}_I-\boldsymbol{\omega}_J)
\right\}
$$
適用例
下図のような2つの剛体が円筒ジョイントで接続された解析モデルを考え、ジョイントの伸縮方向に、伸縮速度に比例する抵抗力を働かせたいとします。
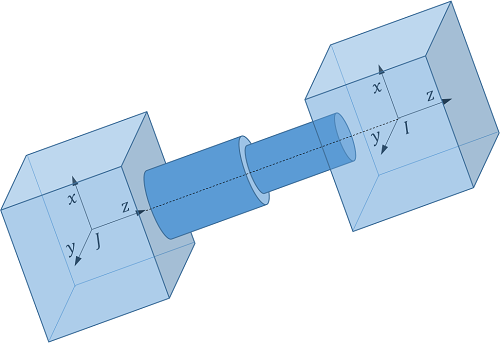
それぞれの剛体に固定された枠 \(I\) と枠 \(J\) の\(z\) 軸が円筒ジョイントの軸と一致しているとすれば、ジョイントの伸縮速度 \(\Delta v\) は、枠 \(J\) から見た、枠 \(J\) に対する枠 \(I\) の相対速度ベクトルの枠 \(J\) による成分表示の \(z\) 方向成分として求められます。すなわち
$$
\begin{align}
\Delta v
& = \left(\mathbf{v}_{J\to JI}^{(J)}\right)_z \\
& =
\begin{bmatrix} 0 & 0 & 1 \end{bmatrix}
(\mathbf{R}_J)^T \left\{
(\dot{\mathbf{r}}_I-\dot{\mathbf{r}}_J)
-\widetilde{\boldsymbol{\omega}}_J(\mathbf{r}_I-\mathbf{r}_J)\right\} \\
& =
(\mathbf{b}_J)^T \left\{
(\dot{\mathbf{r}}_I-\dot{\mathbf{r}}_J)
-\widetilde{\boldsymbol{\omega}}_J(\mathbf{r}_I-\mathbf{r}_J)\right\}
\end{align}
$$
です。ここで、\(\mathbf{b}_J\) は \(\mathbf{R}_J\) の3列目による代数ベクトルで、枠 \(J\) の \(z\) 軸方向単位ベクトルの成分表示に相当します。
この伸縮速度 \(\Delta v\) を用いて、抵抗力の比例定数を \(c\) とすれば、物体 \(I\) と \(J\) に働く抵抗力の全体基準枠による成分表示はそれぞれ、
$$ \mathbf{F}_I = -c\Delta{v}\mathbf{b}_J, \quad \mathbf{F}_J = -\mathbf{F}_I $$
となり、この力を解析モデルに定義すればよいでしょう。
まとめ
この記事では、回転する座標系から見た、2つの移動枠の相対位置、相対速度、相対加速度、相対角速度、相対角加速度の計算方法を示しました。相対速度、相対加速度、相対角加速度は、回転する座標系から見た場合、単なる絶対量の差とは異なるので間違えやすいです。ご参考になれば幸いです。



コメント