「質点の運動や剛体の並進運動の力学は分かるけれど、剛体の回転運動は苦手」という方、結構多くいらっしゃるのではないでしょうか。実際に、3次元の剛体の回転運動の運動学・力学は、なかなか難解です。しかし、次の3つの事柄をきちんと理解すれば、回転運動を含む任意の3次元の運動を、かなり自在に計算することができるようになります。
- ベクトルの成分表示と座標変換
- 回転行列
- 角速度ベクトルと回転行列の時間微分
1つ目の「ベクトルの成分表示と座標変換」と2つ目の「回転行列」については、既に以前の記事で詳しく解説しました(下の関連記事を参照してください)。本記事では、3つ目の「角速度ベクトルと回転行列の時間微分」について解説します。
角速度とは(固定軸回転の場合)
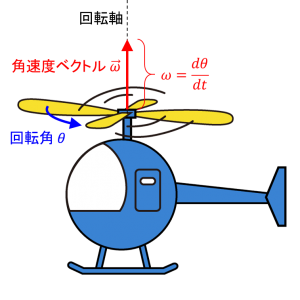
物体の角速度とは、物体の回転する速さを表す量で、単位時間あたりに回転する角度で定義されます。下図のように、ヘリコプターのローター(回転翼)が固定軸の周りで、 \(\Delta t\) 秒間に \(\Delta \theta\) ラジアン(rad)だけ回転するとき、\(\bar{\omega}=\Delta\theta/\Delta t\) をローターの平均角速度(単位:rad/s)といい、\(\Delta t\) が \(0\) に近づくときの \(\bar{\omega}\) の極限値、つまり
$$ \omega=\lim_{\Delta t \to 0} \frac{\Delta\theta}{\Delta t} \equiv \frac{d\theta}{dt} $$
をローターの瞬間角速度(単位:rad/s)といいます。瞬間角速度は回転角の時間微分です。
 ©dak, source: illust image
©dak, source: illust image
角速度ベクトルとは(固定軸回転の場合)
物体が固定軸の周りに角速度 \(\omega\) で回転しているとき、回転軸と並行で、回転に対して右ねじが進む向きに、大きさが \(\omega\) のベクトル \(\vec{\omega}\) を考え、これを角速度ベクトルといいます。角速度ベクトルは、3次元空間における回転軸の向きと、回転の速さおよび回転方向を同時に表します。
 ©dak, source: illust image
©dak, source: illust image
任意回転の角速度ベクトル
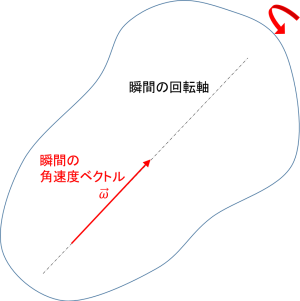
ここまでは、物体が固定軸のまわりを回転する場合に、物体の角速度と角速度ベクトルがどのように定義されるかを見ました。では、物体が(固定軸まわりではなく)任意に回転する場合、角速度と角速度ベクトルはどのように定義されるのでしょうか。
実は、任意に回転する物体であっても、各瞬間には回転軸が存在し、その軸周りの回転角の時間微分によって瞬間角速度を定義できます。そして、瞬間回転軸と瞬間角速度から、その瞬間の角速度ベクトルを定義することができます。
角速度ベクトルの成分表示
角速度ベクトルを成分表示するとき、基準となる座標系は主に2つ考えられます。1つは空間に固定され静止している座標系(全体基準枠)、もう1つは物体に固定され物体とともに回転する座標系(物体基準枠)です。
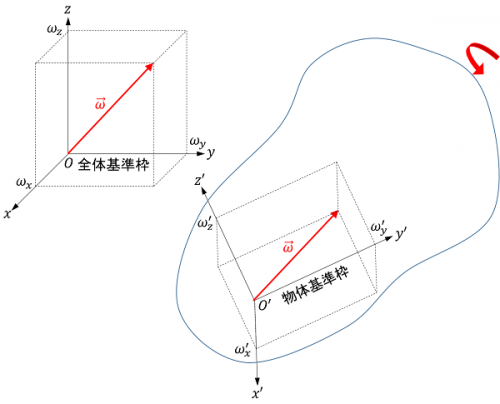
角速度ベクトル \(\vec{\omega}\) の全体基準枠と物体基準枠による成分表示をそれぞれ
$$\boldsymbol{\omega}=\begin{bmatrix} \omega_x \\ \omega_y \\ \omega_z \end{bmatrix}, \quad \boldsymbol{\omega}^\prime=\begin{bmatrix} \omega_x^\prime \\ \omega_y^\prime \\ \omega_z^\prime \end{bmatrix}$$
とすると、一般に \(\boldsymbol{\omega}\ne\boldsymbol{\omega}^\prime\) です。全体基準枠に対する物体基準枠の回転行列を \(\mathbf{R}\) とすれば、
$$ \boldsymbol{\omega} = \mathbf{R}\boldsymbol{\omega}^\prime \tag{1}$$
が成り立ちます。また、\(\boldsymbol{\omega}\) と \(\boldsymbol{\omega}^\prime\) のチルダ行列の間には次の関係があります。
$$ \tilde{\boldsymbol{\omega}} = \mathbf{R}\tilde{\boldsymbol{\omega}^\prime}\mathbf{R}^T \tag{2} $$
式(1)と(2)の導出およびチルダ行列については、以下の記事を参照してください。
剛体に固定されたベクトルの時間微分
下図のように、ある瞬間に角速度ベクトル \(\vec{\omega}\) で回転する剛体と、この剛体に固定されたベクトル \(\vec{a}\) を考えます。
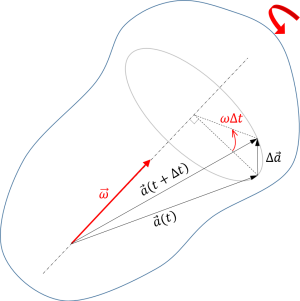
全体基準枠から見た、ベクトル \(\vec{a}\) の時間微分は次式で与えられます。
$$ \dot{\vec{a}} \equiv \frac{d\vec{a}}{dt} \equiv \lim_{\Delta t \to 0} \frac{\Delta \vec{a}}{\Delta t} = \vec{\omega}\times\vec{a} \tag{3} $$
式(3)は、図より幾何学的に導出することができます。
ベクトル \(\vec{\omega}\)、\(\vec{a}\) の全体基準枠による成分表示をそれぞれ \(\boldsymbol{\omega}\)、\(\mathbf{a}\) とすると、式(3)と同等な代数ベクトルの関係式は次式になります。
$$ \dot{\mathbf{a}} = \boldsymbol{\omega}\times{\mathbf{a}} = \tilde{\boldsymbol{\omega}}\mathbf{a} \tag{4} $$
式(4)の関係は、回転行列の記事で紹介した無限小回転の回転行列を使って導出することもできます。ベクトル \(\mathbf{a}\) が微小時間 \(dt\) の間に \(\mathbf{a}(t)\) から \(\mathbf{a}(t+dt)\) へ移動したとすると、軸方向ベクトル \(\boldsymbol{\omega}/|\boldsymbol{\omega}|\)、微小回転角 \(|\boldsymbol{\omega}|dt\) の無限小回転の回転行列を用いて、
$$\mathbf{a}(t+dt) = \underbrace{\left( \mathbf{I}+\frac{\tilde{\boldsymbol{\omega}}}{|\boldsymbol{\omega}|}(|\boldsymbol{\omega}|dt) \right)}_{無限小回転の回転行列}\mathbf{a}(t) = \mathbf{a}(t)+\tilde{\boldsymbol{\omega}}\mathbf{a}(t)dt$$
ですから、
$$ \dot{\mathbf{a}} \equiv \frac{\mathbf{a}(t+dt)-\mathbf{a}(t)}{dt} = \tilde{\boldsymbol{\omega}}\mathbf{a} $$
が得られます。
回転行列の時間微分
では、いよいよ、回転行列の時間微分と角速度ベクトルの関係式を導出しましょう。
座標系 \(O-x^{\prime}y^{\prime}z^{\prime}\) が座標系 \(O-xyz\) に対して角速度ベクトル \(\vec{\omega}\) で回転し、\(\vec{\omega}\) の座標系 \(O-xyz\) と \(O-x^{\prime}y^{\prime}z^{\prime}\) による成分表示をそれぞれ \(\boldsymbol{\omega}\)、\(\boldsymbol{\omega}^\prime\) とします。
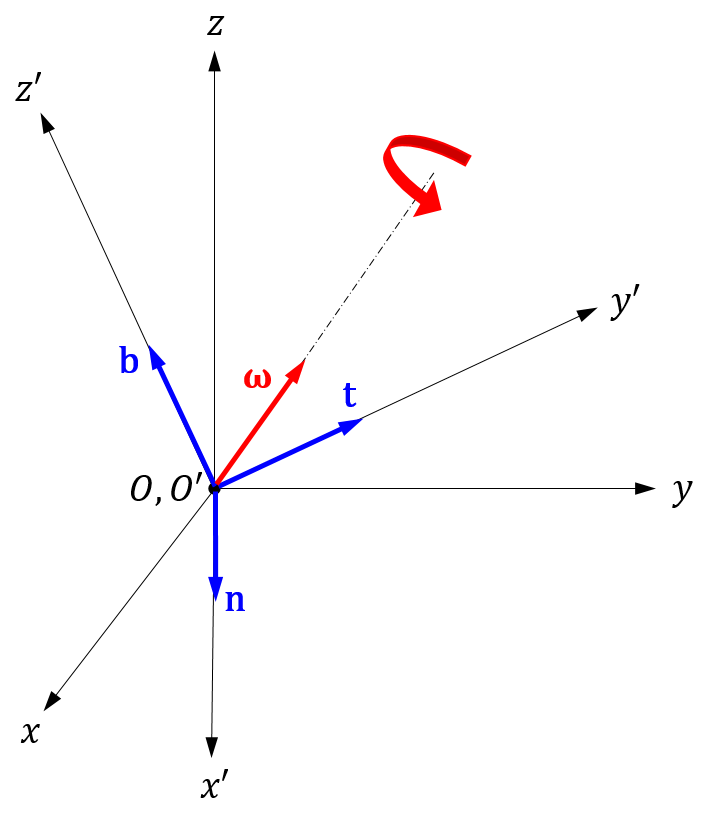
座標系 \(O-x^{\prime}y^{\prime}z^{\prime}\) の回転行列 \(\mathbf{R}\) は、\(x^\prime\)、\(y^\prime\)、\(z^\prime\)軸方向の単位ベクトルの成分表示をそれぞれ \(\mathbf{n}\)、\(\mathbf{t}\)、\(\mathbf{b}\)とすると
$$\mathbf{R}=\begin{bmatrix} \mathbf{n} & \mathbf{t} & \mathbf{b} \end{bmatrix}$$
です。回転行列の時間微分は式(4)を用いて、
$$\begin{align}\dot{\mathbf{R}} &= \begin{bmatrix} \dot{\mathbf{n}} & \dot{\mathbf{t}} & \dot{\mathbf{b}} \end{bmatrix} \\ &= \begin{bmatrix} \tilde{\boldsymbol{\omega}}\mathbf{n} & \tilde{\boldsymbol{\omega}}\mathbf{t} & \tilde{\boldsymbol{\omega}}\mathbf{b} \end{bmatrix} \\ &= \tilde{\boldsymbol{\omega}}\underbrace{\begin{bmatrix} \mathbf{n} & \mathbf{t} & \mathbf{b} \end{bmatrix}}_{\mathbf{R}} \end{align} $$
つまり、
$$\dot{\mathbf{R}} = \tilde{\boldsymbol{\omega}}\mathbf{R} \tag{5} $$
となります。式(5)を \(\tilde{\boldsymbol{\omega}}\) について解けば、
$$\tilde{\boldsymbol{\omega}}=\dot{\mathbf{R}}\mathbf{R}^{T} \tag{6}$$
を得ます。また、式(2)と(5)から、\(\boldsymbol{\omega}^\prime\) に関する式、
$$\dot{\mathbf{R}} = \mathbf{R}\tilde{\boldsymbol{\omega}^\prime} \tag{7}$$
$$\tilde{\boldsymbol{\omega}^\prime}=\mathbf{R}^{T}\dot{\mathbf{R}} \tag{8}$$
を得ることができます。
式(5)~(8)は、回転行列の時間微分と角速度ベクトルの関係を表す便利な公式です。式(5)(7)はポアソンの微分方程式(Poisson differential equation)と呼ばれています。[1]
応用例:移動する剛体上の点の速度・加速度
以上の結果の応用例として、下図のように、空間中を任意に移動する剛体上の点 \(P\) の速度と加速度を求めてみましょう。
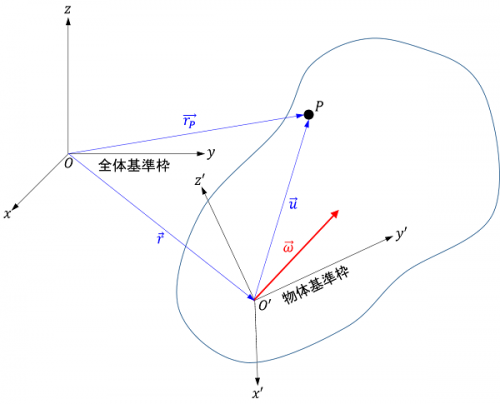
全体基準枠に対する物体基準枠原点の位置ベクトルを \(\vec{r}\)、全体基準枠に対する点 \(P\) の位置ベクトルを \(\vec{r}_P\)、物体基準枠に対する点 \(P\) の位置ベクトルを \(\vec{u}\) 、剛体の角速度ベクトルを \(\vec{\omega}\)、物体基準枠の回転行列を \(\mathbf{R}\) とします。また、\(\vec{r}, \vec{r}_P, \vec{\omega}\) の全体基準枠による成分表示をそれぞれ \(\mathbf{r}, \mathbf{r}_P, \boldsymbol{\omega}\)、\(\vec{u}\) の物体基準枠による成分表示を \(\mathbf{u}^\prime\) とします。
点 \(P\) の位置ベクトルは次のように表せます。
$$\mathbf{r}_P=\mathbf{r}+\mathbf{R}\mathbf{u}^\prime\tag{9}$$
点 \(P\) が剛体に固定されている場合
点 \(P\) が剛体に固定されている場合、\(\mathbf{u}^\prime\) は一定です。
式(9)を時間微分し、式(5)を適用すれば、点 \(P\) の速度ベクトルが次のように求まります。
$$
\begin{align}
\dot{\mathbf{r}}_P &= \dot{\mathbf{r}}+\dot{\mathbf{R}}\mathbf{u}^\prime \\
& = \dot{\mathbf{r}}+\tilde{\boldsymbol{\omega}}\mathbf{R}\mathbf{u}^\prime \tag{10}\\
\end{align}
$$
式(10)をさらに時間微分し、式(5)を再度適用すれば、点 \(P\) の加速度ベクトルが次のように求まります。
$$
\begin{align}
\ddot{\mathbf{r}}_P
&= \ddot{\mathbf{r}} + \tilde{\dot{\boldsymbol{\omega}}}\mathbf{R}\mathbf{u}^\prime + \tilde{\boldsymbol{\omega}}\dot{\mathbf{R}}\mathbf{u}^\prime \\
& = \ddot{\mathbf{r}} + \tilde{\dot{\boldsymbol{\omega}}}\mathbf{R}\mathbf{u}^\prime + \tilde{\boldsymbol{\omega}}\tilde{\boldsymbol{\omega}}\mathbf{R}\mathbf{u}^\prime \tag{11}\\
\end{align}
$$
式(11)の第1項は全体基準枠に対する物体基準枠原点の加速度です。第2項、第3項は物体基準枠原点に対する点 \(P\) の加速度で、それぞれ接線加速度、求心加速度と呼ばれるものです。
ちなみに、式(5)の代わりに式(7)を用いれば、物体基準枠による角速度成分を用いて、点 \(P\) の速度、加速度を求めることができます。
点 \(P\) が剛体上を動く場合
点 \(P\) が剛体上を動く場合、\(\mathbf{u}^\prime\) は時間によって変化しますので、\(\mathbf{u}^\prime\) の時間微分も考慮に入れます。
式(9)を時間微分し、式(5)を適用すれば、点 \(P\) の速度ベクトルが次のように求まります。
$$
\begin{align}
\dot{\mathbf{r}}_P &= \dot{\mathbf{r}}+\dot{\mathbf{R}}\mathbf{u}^\prime+\mathbf{R}\dot{\mathbf{u}}^\prime \\
& = \dot{\mathbf{r}}+\tilde{\boldsymbol{\omega}}\mathbf{R}\mathbf{u}^\prime+\mathbf{R}\dot{\mathbf{u}}^\prime \tag{12}\\
\end{align}
$$
式(12)をさらに時間微分し、式(5)を再度適用すれば、点 \(P\) の加速度ベクトルが次のように求まります。
$$
\begin{align}
\ddot{\mathbf{r}}_P
&= \ddot{\mathbf{r}}
+ \tilde{\dot{\boldsymbol{\omega}}}\mathbf{R}\mathbf{u}^\prime
+ \tilde{\boldsymbol{\omega}}\dot{\mathbf{R}}\mathbf{u}^\prime
+ \tilde{\boldsymbol{\omega}}\mathbf{R}\dot{\mathbf{u}}^\prime
+ \dot{\mathbf{R}}\dot{\mathbf{u}}^\prime
+ \mathbf{R}\ddot{\mathbf{u}}^\prime \\
& = \ddot{\mathbf{r}}
+ \tilde{\dot{\boldsymbol{\omega}}}\mathbf{R}\mathbf{u}^\prime
+ \tilde{\boldsymbol{\omega}}\tilde{\boldsymbol{\omega}}\mathbf{R}\mathbf{u}^\prime
+ \mathbf{R}\ddot{\mathbf{u}}^\prime
+ 2\tilde{\boldsymbol{\omega}}\mathbf{R}\dot{\mathbf{u}}^\prime
\tag{13}\\
\end{align}
$$
式(13)の第4項は物体基準枠に対する点 \(P\) の加速度です。第5項はコリオリの加速度と呼ばれる加速度成分です。
参考文献
[1] 日本機械学会編. マルチボディダイナミクス(1)基礎理論, コンピュータダイナミクスシリーズ3, コロナ社, 2006.
[2] Shabana, A. A. Dynamics of Multibody Systems. 4th edition, Cambridge, 2013.






コメント
[…] $T_{pkr}$ の導出がちょっと厄介です。このサイトを参考にすると、回転後の座標系 $Sigma_p$ での角速度ベクトル $omega_p$ […]