オイラー角(Euler/Eulerian angles)は、3次元空間における剛体または参照座標系の回転姿勢を表す方法の一つです。独立な3つの角度の組で回転姿勢を表し、便利で分かりやすいので、力学やコンピュータグラフィックスでもよく使われています。この記事では、オイラー角の定義と性質、回転行列や角速度ベクトルとの関係などについて詳しく解説します。
はじめに
基準の座標系に対する剛体の回転姿勢を記述したいとき、1つの方法としては回転行列があります。回転行列については以前の記事で詳しく解説しました。
回転行列はとても便利なのですが、回転姿勢を記述する方法としては欠点があります。それは、剛体の回転自由度が3なのに対して、回転行列には9個の変数があり、それらは6個の拘束条件で相互に依存しているため、回転行列を一般化座標として剛体の運動方程式を導こうとすると非常に複雑になってしまうことです。また、単に9個の変数は多すぎで、例えば飛行機のダッシュボードに回転行列の9個の数値が表示されても、機体がどっちを向いているのかパイロットがすぐに把握するのは難しいでしょう。
では、回転行列の代わりに、もっと少ない変数で(できれば独立な3つの変数で)回転姿勢を記述する方法はないのでしょうか?その問いへの1つの答えがオイラー角です。
オイラー角にはいくつかの異なる型が存在しますが、この記事では主に、航空工学の分野でよく採用されている「内的(intrinsic)回転」による「\(z-y-x\)」型のオイラー角(タイト・ブライヤン角)を取り上げます。オイラー角の型については記事の最後で言及しますが、他の型のオイラー角も基本的には同様に考えることができます。
オイラー角の定義
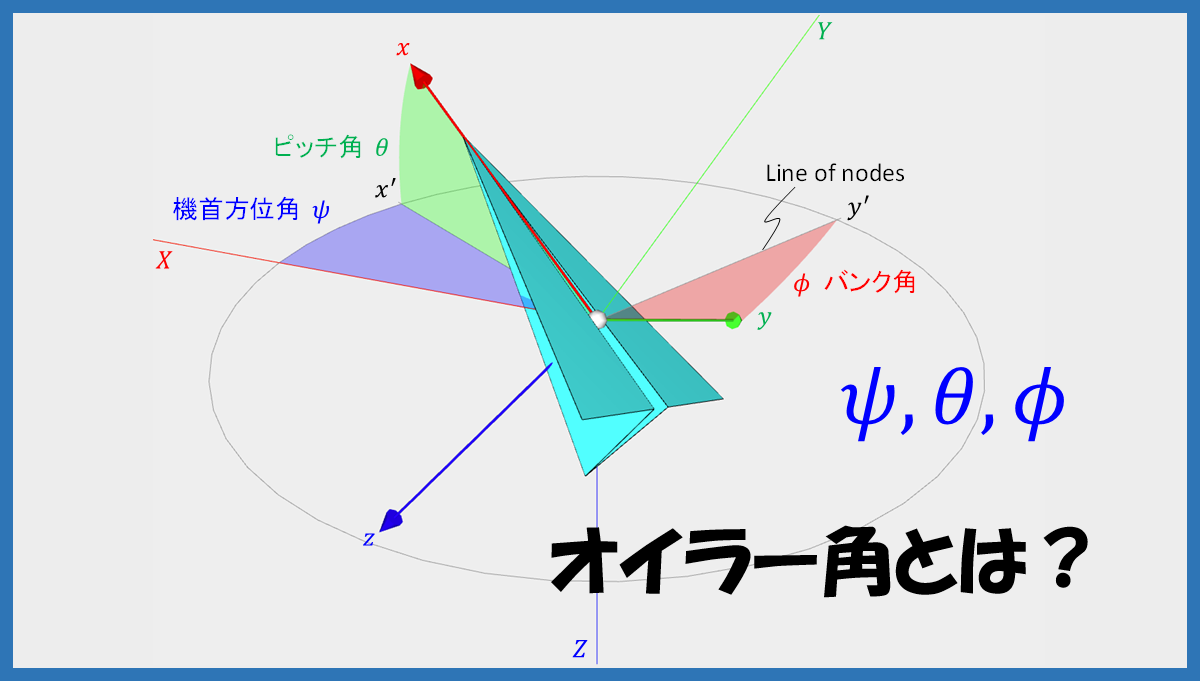
下図のように、地上に固定された座標系 \(XYZ\)(固定座標系)と飛行機の機体に固定された座標系 \(xyz\)(機体座標系)を考えます。飛行機の機体座標系 \(xyz\) は通常、\(x\) 軸を機首方向に、\(z\) 軸を下方向に、\(y\) 軸を他の2つの軸と垂直に右翼方向に取ります。また、今は、飛行機の回転姿勢だけを問題とするので、2つの座標系の原点は一致させて考えます。最初、2つの座標系が一致している状態から、以下の①~③のように機体座標系の座標軸周りの3つの連続する回転を考えます。
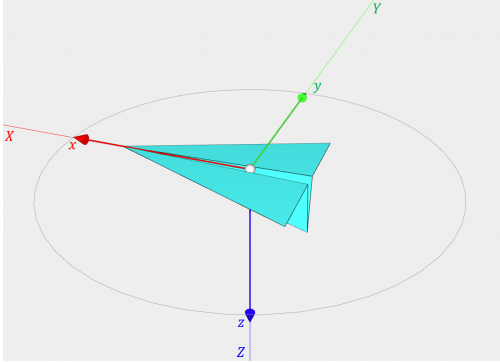
初期姿勢
① \(z\) 軸周りに \(\psi\) だけ回転
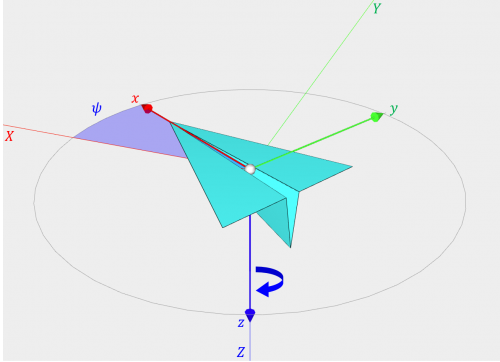
機体座標系の \(z\) 軸周りに回転
② \(y\) 軸周りに \(\theta\) だけ回転
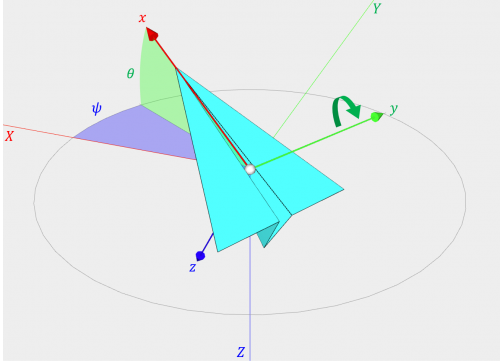
機体座標系の \(y\) 軸周りに回転
③ \(x\) 軸周りに \(\phi\) だけ回転
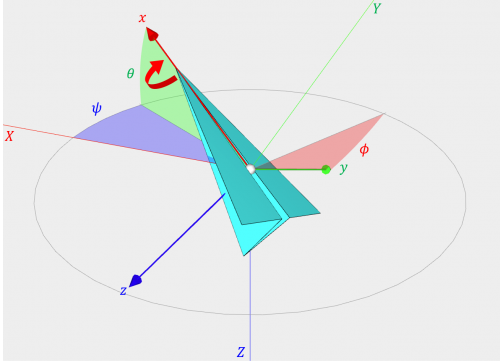
機体座標系の \(x\) 軸周りに回転
飛行機は、この①~③の連続回転により任意の回転姿勢に持っていくことができます。そこで、この3つの回転角の組 \((\psi, \theta, \phi)\) をオイラー角(Euler/Eulerian angles)と呼び、回転姿勢の記述に用いることができます。飛行機の場合、\(\psi\) を機首方位角(heading angle)、\(\theta\) をピッチ角(attitude angle)、\(\phi\) をバンク角(bank angle)と呼びます。[1]
オイラー角は上記のように、3つの連続回転の回転角として理解することができますが、機体座標系の軸の向きから直接求めることもできます。下図から分かるように、\(x\) 軸を \(XY\) 平面に投影した軸を \(x^{\prime}\) 軸とすれば、\(X\) 軸と \(x^{\prime}\) 軸のなす角が機首方位角 \(\psi\)、\(x^{\prime}\) 軸と \(x\) 軸 のなす角がピッチ角 \(\theta\) となります。ピッチ角 \(\theta\) の回転軸 \(y^{\prime}\) は \(XY\) 平面上にあり、「Line of nodes」と呼ばれます。\(y^{\prime}\) 軸と \(y\) 軸のなす角がバンク角 \(\phi\) となります。
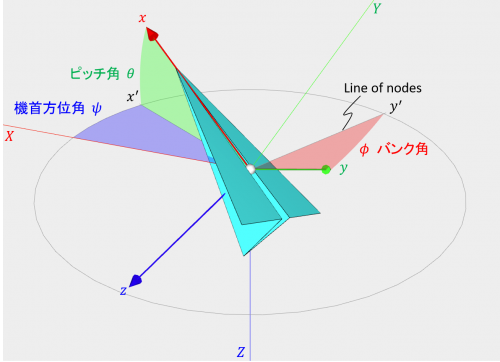
飛行機の回転姿勢とオイラー角
回転角に制限を付けなければ、オイラー角は一意ではありません。例えば、オイラー角 \((0, \pi/4, 0)\) と オイラー角 \((\pi, 3\pi/4, \pi)\) は同じ回転姿勢を表します。しかし、例えば次のように回転角に値域を設ければ、次項で説明する特異姿勢の場合を除いてオイラー角は一意となります。
$$ 0 \leq \psi < 2\pi, \quad -\frac{\pi}{2} \leq \theta \leq \frac{\pi}{2}, \quad 0 \leq \phi < 2\pi $$
以上、オイラー角の定義を飛行機の例で示しましたが、オイラー角は飛行機に限らず、一般の剛体の回転姿勢を記述するのに用いることができます。
ちなみに、上の図を作成する際に用いた「オイラー角可視化ツール」をウェブアプリとして公開しているので、良かったら利用してみてください。
特異姿勢とジンバルロック
下図のように、ピッチ角 \(\theta\) が \(\pi/2\)(90度)の時、機首方位角 \(\psi\) とバンク角 \(\phi\) の値にかかわらず、機体座標系の \(x\) 軸は固定座標系の \(Z\) 軸と並行になります。このとき、\(\psi\) と \(\phi\) はどちらも \(Z\) 軸まわりの回転に寄与します。
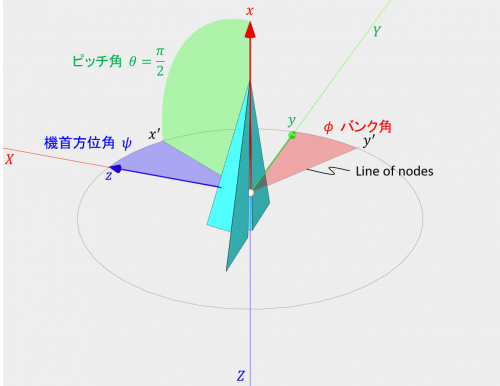
特異姿勢
この場合、一意の \(\psi\) と \(\phi\) を決定できません。例えば、次の3組のオイラー角で表される飛行機の回転姿勢は全く同じになります。
$$
\left(0, \frac{\pi}{2}, 0\right), \quad
\left(\frac{\pi}{4}, \frac{\pi}{2}, \frac{\pi}{4}\right), \quad
\left(\pi, \frac{\pi}{2}, \pi\right)
$$
つまり、 \(\theta=\pi/2\) の時、\(\psi\) と \(\phi\) は不定です。しかし、図や上の例からも分かるように、\(\psi-\phi\) は決定されます。同様に、\(\theta=-\pi/2\) の時、\(\psi\) と \(\phi\) は不定となりますが、\(\psi+\phi\) は決定されます。
通常、オイラー角は3つの独立変数で自由度3の回転を表すことができますが、\(\theta=\pm\pi/2\) のときは、\(\psi\) と \(\phi\) が従属となり、オイラー角が表現できる回転自由度が1つ欠落してしまう状態となります。この回転自由度が欠落してしまう姿勢を、特異姿勢(singular orientation)と呼びます。特異姿勢では、自由度が欠落しているので、回転できない方向が存在します。上図の \(\theta=\pi/2\) の特異姿勢の状態では、オイラー角を変化させることで、\(x^\prime\) 軸周りに回転させることはできません。この状態のことをジンバルロックと呼びます。
ただし、ここで言う特異姿勢やジンバルロックは、オイラー角の特性であり、飛行機のような自由に回転できる物体の特性ではないことに注意してください。飛行機が垂直になったとしても、飛行機の物理的な回転自由度は減りませんし、\(x^\prime\) 軸周りに回転することも可能です。一方、下図のジンバルのように物理的に拘束された物体では、物理的な特異姿勢やジンバルロックが存在します。

https://commons.wikimedia.org/wiki/File:Gimbal_Lock_Plane.gif
飛行機のように自由に回転できる物体の運動をオイラー角を用いて数値計算する場合には、特異姿勢近傍の計算に注意する必要があります。特異姿勢近傍では小さな回転姿勢の変化が、大きなオイラー角の変化となることがあり、数値計算を正確に行うことが難しくなるからです。例えば、下図の2つの回転姿勢の違いは僅かですが、オイラー角は大きく異なります。
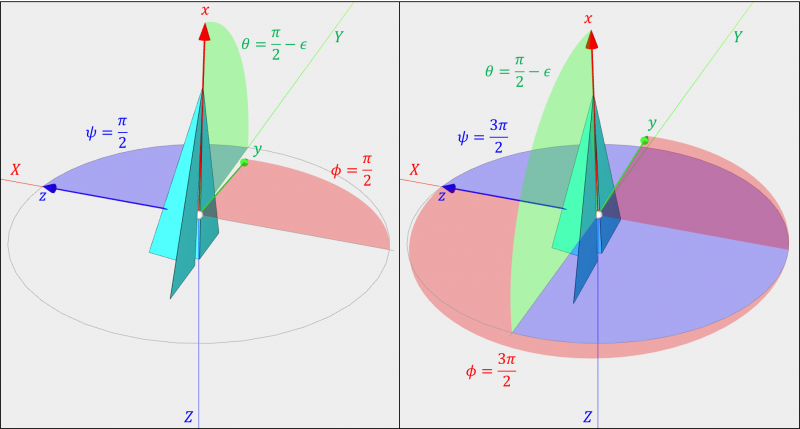
特異姿勢近傍ではオイラー角が大きく変化
オイラー角を回転行列に変換
オイラー角と回転行列はともに剛体の回転姿勢を表しますから、互いに変換することができます。オイラー角が与えられたとき、同等の回転姿勢を表す回転行列を求めてみましょう。
回転行列の記事で示した、座標軸周りの回転を表す回転行列の式と連続回転の回転行列の公式を用いれば、オイラー角 \((\psi, \theta, \phi)\) と同等の回転姿勢を表す回転行列は次のように求められます。
$$
\begin{align}
\mathbf{R}
&=
\underbrace{\begin{bmatrix} \cos{\psi} & -\sin{\psi} & 0 \\ \sin{\psi} & \cos{\psi} & 0 \\ 0 & 0 & 1 \end{bmatrix}}_{z軸周り回転}
\underbrace{\begin{bmatrix} \cos{\theta} & 0 & \sin{\theta} \\ 0 & 1 & 0 \\ -\sin{\theta} & 0 & \cos{\theta} \end{bmatrix}}_{y軸周り回転}
\underbrace{\begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos{\phi} & -\sin{\phi} \\ 0 & \sin{\phi} & \cos{\phi} \end{bmatrix}}_{x軸周り回転} \\
&=
\begin{bmatrix}
c_\psi c_\theta & c_\psi s_\theta s_\phi – c_\phi s_\psi & s_\psi s_\phi + c_\psi c_\phi s_\theta \\
c_\theta s_\psi & c_\psi c_\phi + s_\psi s_\theta s_\phi & c_\phi s_\psi s_\theta – c_\psi s_\phi \\
-s_\theta & c_\theta s_\phi & c_\theta c_\phi
\end{bmatrix}\tag{1}
\end{align}
$$
ここで、最後の式は簡略記法で書かれており、\(s\) と \(c\) は \(\sin\) と \(\cos\) を意味します。(例えば、\(s_\psi\) は \(\sin\psi\) を意味します。)
回転行列をオイラー角に変換
逆に、回転行列が与えられたときに、同等の回転姿勢を表すオイラー角を求めてみましょう。
回転行列が次のように与えられたとします。
$$
\mathbf{R} =
\begin{bmatrix}
R_{11} & R_{12} & R_{13} \\
R_{21} & R_{22} & R_{23} \\
R_{31} & R_{32} & R_{33}
\end{bmatrix}\tag{2}
$$
式(1)と(2)の \((3,1)\) 成分同士を比較すると、
$$ \sin\theta = -R_{31} \tag{3}$$
を得ます。\(\theta\) の値域を \(-\pi/2 \leq \theta \leq \pi/2\) とすれば、式(3)により、\(\theta\) の値を一意に求めることができます。残りは \(\psi\) と \(\phi\) の値ですが、以下の①~③のように場合分けをします。
① \(|R_{31}| \neq 1\) のとき(\(\theta \neq \pm \pi/2\) のとき)
式(1)と(2)の \((1,1)\) 成分同士と \((2,1)\) 成分同士を比較すると、
$$
\begin{cases}
\cos\psi & = & R_{11}/\cos\theta \\
\sin\psi & = & R_{21}/\cos\theta
\end{cases} \tag{5}
$$
を得て、式(5)から \(\psi\) を求めることができます。また、式(1)と(2)の \((3,3)\) 成分同士と \((3,2)\) 成分同士を比較すると、
$$
\begin{cases}
\cos\phi & = & R_{33}/\cos\theta \\
\sin\phi & = & R_{32}/\cos\theta
\end{cases} \tag{6}
$$
を得て、式(6)から \(\phi\) を求めることができます。
② \(R_{31} = 1\) のとき(\(\theta = -\pi/2\) のとき)
特異姿勢となりますから、\(\psi\) と \(\phi\) は不定です。しかし、式(2)と(3)の \((1,2)\) 成分と \((2,2)\) 成分の比較から、
$$
\begin{cases}
\cos(\psi+\phi) & = & R_{22} \\
\sin(\psi+\phi) & = & -R_{12} \\
\end{cases} \tag{7}
$$
を得て、式(7)から \(\psi+\phi\) を求めることができます。
③ \(R_{31} = -1\) のとき(\(\theta = \pi/2\) のとき)
特異姿勢となりますから、\(\psi\) と \(\phi\) は不定です。しかし、式(2)と(3)の \((1,2)\) 成分と \((2,2)\) 成分の比較から、
$$
\begin{cases}
\cos(\psi-\phi) & = & R_{22} \\
\sin(\psi-\phi) & = & -R_{12} \\
\end{cases} \tag{8}
$$
を得て、式(8)から \(\psi-\phi\) を求めることができます。
オイラー角の時間微分を角速度ベクトルに変換
物体の回転運動をオイラー角を用いて解析する場合には、オイラー角の時間微分 \(\dot{\psi}, \dot{\theta}, \dot{\phi}\) と物体の角速度ベクトルの関係を知る必要があります。
角速度ベクトルについては以下の関連記事で詳しく解説していますので、そちらを参照してください。
オイラー角の時間微分と角速度ベクトルの関係は、式(1)の回転行列を時間微分して、上記関連記事で紹介した角速度ベクトルと回転行列の時間微分の関係式 \(\tilde{\boldsymbol{\omega}} = \dot{\mathbf{R}}\mathbf{R}^T\) または \(\tilde{\boldsymbol{\omega}^\prime} = \mathbf{R}^T\dot{\mathbf{R}}\) へ代入することによって代数的に求めることもできますが、計算がかなり面倒です。
そこで、ここでは、図から直接求めてみましょう。オイラー角の3つの角それぞれの変化による角速度ベクトルを \(\vec{\omega}_\psi\)、\(\vec{\omega}_\theta\)、\(\vec{\omega}_\phi\) とすると、大きさはそれぞれ \(\dot{\psi}\)、\(\dot{\theta}\)、\(\dot{\phi}\)であり 、向きは下図に示すようになります。
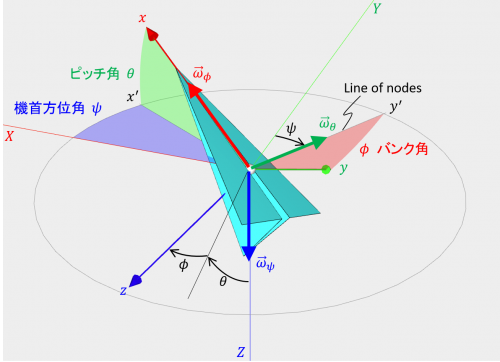
各オイラー角の変化による角速度ベクトル
図より、これらの角速度ベクトルの固定座標系 \(XYZ\) による成分表示は、
$$
\boldsymbol{\omega}_\psi =
\begin{bmatrix}
0 \\
0 \\
\dot{\psi}
\end{bmatrix}, \quad
\boldsymbol{\omega}_\theta =
\begin{bmatrix}
-\dot{\theta}\sin{\psi} \\
\dot{\theta}\cos{\psi} \\
0
\end{bmatrix}, \quad
\boldsymbol{\omega}_\phi =
\begin{bmatrix}
\dot{\phi}\cos{\theta}\cos{\psi} \\
\dot{\phi}\cos{\theta}\sin{\psi} \\
-\dot{\phi}\sin{\theta}
\end{bmatrix}
$$
また、機体座標系 \(xyz\) による成分表示は、
$$
\boldsymbol{\omega}_{\psi}^{\prime} =
\begin{bmatrix}
-\dot{\psi}\sin{\theta} \\
\dot{\psi}\cos{\theta}\sin{\phi} \\
\dot{\psi}\cos{\theta}\cos{\phi}
\end{bmatrix}, \quad
\boldsymbol{\omega}_{\theta}^{\prime} =
\begin{bmatrix}
0 \\
\dot{\theta}\cos{\phi} \\
-\dot{\theta}\sin{\phi}
\end{bmatrix}, \quad
\boldsymbol{\omega}_{\phi}^{\prime} =
\begin{bmatrix}
\dot{\phi} \\
0 \\
0
\end{bmatrix}
$$
となることが分かります。飛行機の角速度ベクトル \(\vec{\omega}\) は各角速度ベクトルの和
$$ \vec{\omega} = \vec{\omega}_\psi + \vec{\omega}_\theta + \vec{\omega}_\phi $$
ですから、\(\vec{\omega}\) の固定座標系 \(XYZ\) による成分表示は、
$$
\begin{align}
\boldsymbol{\omega}
& =
\boldsymbol{\omega}_\psi + \boldsymbol{\omega}_\theta + \boldsymbol{\omega}_\phi =
\begin{bmatrix}
\dot{\phi}\cos{\theta}\cos{\psi}-\dot{\theta}\sin{\psi} \\
\dot{\phi}\cos{\theta}\sin{\psi}+\dot{\theta}\cos{\psi} \\
\dot{\psi}-\dot{\phi}\sin{\theta}
\end{bmatrix} \\
& =
\begin{bmatrix}
0 & -\sin{\psi} & \cos{\theta}\cos{\psi} \\
0 & \cos{\psi} & \cos{\theta}\sin{\psi} \\
1 & 0 & -\sin{\theta}
\end{bmatrix}
\begin{bmatrix}
\dot{\psi} \\
\dot{\theta} \\
\dot{\phi}
\end{bmatrix} \tag{9}
\end{align}
$$
また、\(\vec{\omega}\) の機体座標系 \(xyz\)による成分表示は、
$$
\begin{align}
\boldsymbol{\omega}^\prime
& =
\boldsymbol{\omega}_\psi^\prime + \boldsymbol{\omega}_\theta^\prime + \boldsymbol{\omega}_\phi^\prime =
\begin{bmatrix}
\dot{\phi}-\dot{\psi}\sin{\theta} \\
\dot{\psi}\cos{\theta}\sin{\phi}+\dot{\theta}\cos{\phi} \\
\dot{\psi}\cos{\theta}\cos{\phi}-\dot{\theta}\sin{\phi}
\end{bmatrix} \\
& =
\begin{bmatrix}
-\sin{\theta} & 0 & 1 \\
\cos{\theta}\sin{\phi} & \cos{\phi} & 0 \\
\cos{\theta}\cos{\phi} & -\sin{\phi} & 0
\end{bmatrix}
\begin{bmatrix}
\dot{\psi} \\
\dot{\theta} \\
\dot{\phi}
\end{bmatrix} \tag{10}
\end{align}
$$
となります。
式(9)と(10)の \(\boldsymbol{\omega}\) と \(\boldsymbol{\omega}^\prime\) の間には、\(\boldsymbol{\omega} = \mathbf{R}\boldsymbol{\omega}^\prime\) の関係があります。
角速度ベクトルをオイラー角の時間微分に変換
式(9)(10)の右辺の係数行列は \(\theta\neq\pm\pi/2\) のとき逆行列をもち、このとき式(9)(10)は \(\dot{\psi}, \dot{\theta}, \dot{\phi}\) について以下のように解くことができます。
$$
\begin{bmatrix}
\dot{\psi} \\
\dot{\theta} \\
\dot{\phi}
\end{bmatrix}
=
\begin{bmatrix}
\frac{\cos{\psi}\sin{\theta}}{\cos{\theta}} & \frac{\sin{\psi}\sin{\theta}}{\cos{\theta}} & 1 \\
-\sin{\psi} & \cos{\psi} & 0 \\
\frac{\cos{\psi}}{\cos{\theta}} & \frac{\sin{\psi}}{\cos{\theta}} & 0
\end{bmatrix}
\boldsymbol{\omega} \tag{11}
$$
$$
\begin{bmatrix}
\dot{\psi} \\
\dot{\theta} \\
\dot{\phi}
\end{bmatrix}
=
\begin{bmatrix}
0 & \frac{\sin{\phi}}{\cos{\theta}} & \frac{\cos{\phi}}{\cos{\theta}} \\
0 & \cos{\phi} & -\sin{\phi} \\
1 & \frac{\sin{\phi}\sin{\theta}}{\cos{\theta}} & \frac{\cos{\phi}\sin{\theta}}{\cos{\theta}}
\end{bmatrix}
\boldsymbol{\omega}^\prime \tag{12}
$$
オイラー角の型
最初にも述べたように、「オイラー角」にはいくつかの異なる型があります。[2]
本記事では、物体に固定された座標系 \(xyz\) を \(z\to y\to x\) の順で座標軸周りに連続回転させたときの3つの回転角でオイラー角を定義しましたが、回転させる座標軸の選び方は他にも考えられます。実のところ、連続で同じ座標軸を選びさえしなければ、どの軸を選んでも任意の回転を表現することができます。そこで、座標軸の選び方の数だけオイラー角の型が存在し、全部で12個あります。
最初の回転と最後の回転で同じ座標軸を使う場合と、3つの回転すべてで違う座標軸を使う場合の2グループに分け、前者を「正規(Proper)オイラー角」、後者を「タイト・ブライヤン角」と区別して呼ぶこともあります。
また、物体座標系 \(xyz\) の座標軸周りに回転する代わりに、固定座標系 \(XYZ\) の座標軸周りに回転する方法もあり、この場合も座標軸の選び方が12通りあります。そこで、物体座標系の座標軸周りに回転する場合を「内的(intrinsic)回転」によるオイラー角、固定座標系の座標軸周りに回転する場合を「外的(extrinsic)回転」によるオイラー角として分類します。以上をまとめると次の表のようになります。
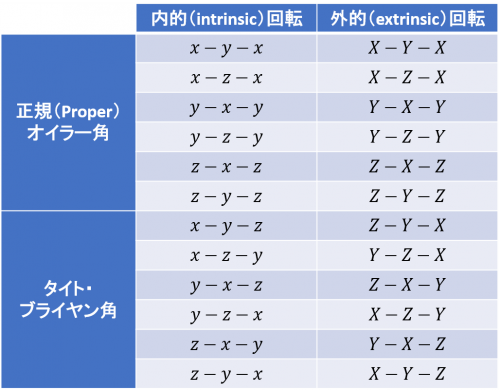
このように、オイラー角には全部で24の型がありますが、考え方や性質は共通しています。この記事では、「内的(intrinsic)回転」による「\(z-y-x\)」型のオイラー角(タイト・ブライヤン角)を扱いましたが、ここで示した結果を別型のオイラー角の結果に変換することが可能です。例えば、この記事の「\(z-y-x\)」型のオイラー角 \((\psi, \theta, \phi)\) の結果から「\(x-y-z\)」型のオイラー角 \((\phi, \theta, \psi)\) の結果を求めるためには、次の置き換えを行います。
$$
X\to -Z,\quad Y\to Y,\quad Z\to X, \\
\psi\to\phi,\quad \theta\to\theta,\quad \phi\to -\psi, \\
x\to -z,\quad y\to y,\quad z\to x
$$
下は、この置き換えを行った図です。
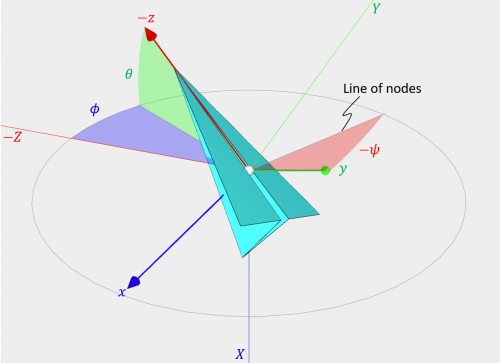
\(x-y-z\) オイラー角
まとめ
この記事では、3次元空間における物体の回転姿勢を表す方法の1つである、オイラー角について解説しました。オイラー角は3自由度の剛体の回転姿勢を、3つの独立変数で表すことができるので、剛体の運動解析で非常に役に立ちます。また、数値の意味が分かりやすいのも利点と言えます。ただし、オイラー角には特異姿勢が存在し、特異姿勢近傍の数値計算には注意が必要です。
この記事がご参考になれば幸いです。
参考文献
[1] Greenwood, D.T. Principles of Dynamics. 2nd edition, Prentice Hall, 1988.
[2] “Euler angles”. Wikipedia: The Free Encyclopedia. https://en.wikipedia.org/wiki/Euler_angles,(参照 2021-07-06 15:17 JST)





コメント