 未分類
未分類 Scilab でジョイスティック入力を行う方法 ~ ダイナミックリンクと call 関数の利用
Scilab 環境でジョイスティック(またはゲームパッド)の入力値を読み取る方法を紹介します。ジョイスティックの入力値を読み取る関数は Scilab の標準モジュールに含まれていないので、C 関数を自作し、Scilab とリンクして call 関数で呼び出す方法を取ります。対象 OS は Windows です。
 未分類
未分類 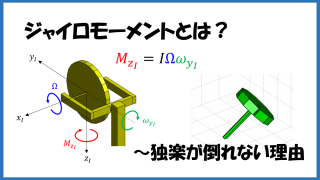 力学
力学 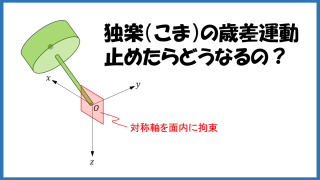 Scilab
Scilab  Scilab
Scilab 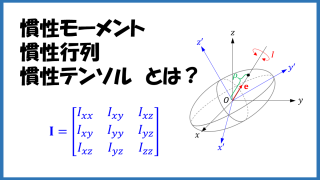 力学
力学 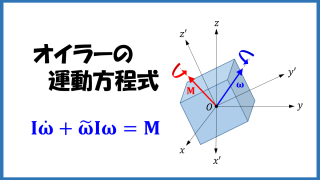 力学
力学  力学
力学  力学
力学  力学
力学  力学
力学