以前の記事で、剛体の回転運動を支配するオイラーの運動方程式について解説しました。この記事では、そのオイラーの運動方程式を用いて剛体の回転運動をシミュレーションする方法を、独楽(こま)のシミュレーションを例として解説します。特に Scilab での実装例を示しますが、方法は一般的なので、他のツールや各種プログラミング言語を使用しても試すことができるはずです。
独楽(こま)のモデル
下図のように、慣性系に固定された座標系 \(O-xyz\) (\(z\) 軸下向き)と、点 \(O\) に支点が固定され、点 \(O\) の周りを自由に回転することができる独楽(こま)を考えます。
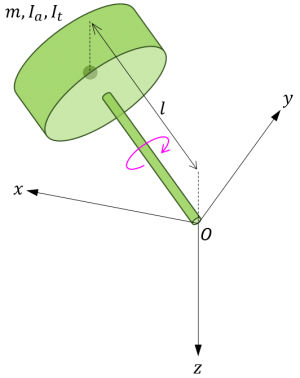
独楽は軸対称の剛体であるとし、支点 \(O\) から重心までの距離を \(l\)、質量を \(m\)、対称軸周りの慣性モーメントを \(I_a\)、重心を通り対称軸に直角な軸周りの慣性モーメントを \(I_t\) とします。独楽には \(z\) 方向の重力が作用するものとし、重力加速度の大きさを \(g\) とします。
この独楽に、任意の初期姿勢と初期角速度を与えたときの運動を、コンピュータを使ってシミュレーションすることを考えてみましょう。
独楽に固定された座標系とオイラー角
一般に、剛体の運動を解析する際には、剛体の回転姿勢を記述するために、剛体に固定された座標系を定めてやる必要があります。座標系の定め方は任意ですが、できるだけ分かりやすいように、または問題が解きやすいように定めると良いです。
この独楽のシミュレーションでは、独楽に固定された座標系 \(O-x^\prime y^\prime z^\prime\) を、下図のように、支点 \(O\) を原点とし、\(x^\prime\) 軸が対称軸と平行で重心を向くように定めることとします。このようにすると、座標系 \(O-x^\prime y^\prime z^\prime\) の座標軸は独楽の支点周りの慣性主軸と一致し、また座標系 \(O-x^\prime y^\prime z^\prime\) の z-y-x型のオイラー角 \((\psi, \theta, \phi)\) がそれぞれ対称軸の方位角(\(\psi\))、傾角(\(\theta\))、独楽の対称軸周りの回転角(\(\phi\))に対応します。
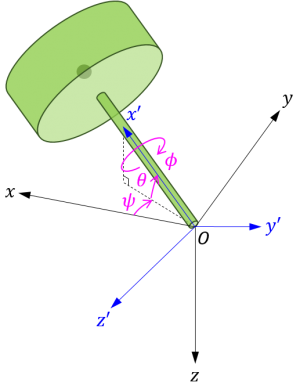
座標系 \(O-xyz\) に対する座標系 \(O-x^\prime y^\prime z^\prime\) の回転行列を \(\mathbf{R}\) とすれば、回転行列とオイラー角の関係は
$$
\mathbf{R} =
\begin{bmatrix}
c_\psi c_\theta & c_\psi s_\theta s_\phi – c_\phi s_\psi & s_\psi s_\phi + c_\psi c_\phi s_\theta \\
c_\theta s_\psi & c_\psi c_\phi + s_\psi s_\theta s_\phi & c_\phi s_\psi s_\theta – c_\psi s_\phi \\
-s_\theta & c_\theta s_\phi & c_\theta c_\phi
\end{bmatrix}\tag{1}
$$
で与えられます。(上式中の、\(s\) と \(c\) は \(\sin\) と \(\cos\) を意味します。例えば、\(s_\psi\) は \(\sin\psi\) を意味します。)
ただし、上記のオイラー角を用いる場合には、\(\theta\) が \(\pm\pi/2\) (±90度)の時、特異姿勢となることに注意しなければなりません。特に、オイラー角を用いて数値計算を行う場合には、特異姿勢近傍では正確な計算が難しくなります。そこで、この独楽のシミュレーションでは、独楽の姿勢を \(\theta\) が \(\pm\pi/2\) (±90度、独楽が垂直の姿勢)近傍にならない範囲に限定することとします。
回転行列とオイラー角については、下の関連記事で詳しく解説していますので参照してください。オイラー角の代わりにオイラーパラメータと呼ばれる量を用いれば、特異姿勢の問題を回避できますが、オイラーパラメータについてはまた別の記事で解説したいと思います。
運動方程式(オイラーの運動方程式)
上記の独楽モデルは、一点が固定された剛体ですから、回転の自由度(自由度3)だけをもち、オイラーの運動方程式によって運動を記述することができます。
独楽に固定された座標系 \(O-x^\prime y^\prime z^\prime\) による独楽の慣性行列を \(\mathbf{I}^\prime\)、独楽の角速度ベクトルの座標系 \(O-x^\prime y^\prime z^\prime\) による成分表示を \(\boldsymbol{\omega}^\prime\)、独楽に働く点 \(O\) 周りの力のモーメントの座標系 \(O-x^\prime y^\prime z^\prime\) による成分表示を \(\mathbf{M}^\prime\) とすると、独楽の運動方程式は
$$ \mathbf{I}^{\prime}\dot{\boldsymbol{\omega}}^{\prime}+\tilde{\boldsymbol{\omega}^\prime}\mathbf{I}^{\prime}\boldsymbol{\omega}^\prime = \mathbf{M}^\prime \tag{2} $$
で与えられます。ここで、\(\tilde{\boldsymbol{\omega}^\prime}\) は \(\boldsymbol{\omega}^\prime\) のチルダ行列を表します。
式(2)は、角速度ベクトル \(\boldsymbol{\omega}^\prime\) を未知変数とする常微分方程式で、これを解けば、独楽の角速度ベクトルの時刻歴が得られます。しかし、角速度ベクトルだけでなく、独楽の回転姿勢の時刻歴も得られなければ、運動のシミュレーションとしては不十分です。そもそも、式(2)の右辺にある \(\mathbf{M}^\prime\) は、後で示すように回転姿勢に依存するので、回転姿勢が求められなければ式(2)の運動方程式を解くこともできません。
では、回転姿勢はどのように求めればよいのでしょうか。答えは、ポアソン微分方程式です。
$$\dot{\mathbf{R}} = \mathbf{R}\tilde{\boldsymbol{\omega}^\prime} \tag{3} $$
ポアソン微分方程式については、次の関連記事を参照してください。
式(2)と(3)の常微分方程式を並列で解くことにより、独楽の角速度ベクトル \(\boldsymbol{\omega}^\prime\) と回転行列 \(\mathbf{R}\) の時刻歴を求めることができます。ただし、回転行列 \(\mathbf{R}\) はその定義より直交行列(\(\mathbf{R}^T\mathbf{R}=\mathbf{I}\))でなければなりませんが、式(3)を単に数値的に積分していくと、誤差により \(\mathbf{R}\) の直交性が失われ、回転行列としての妥当性が損なわれてしまう可能性があります。従って、式(3)を数値的に解く場合には、 \(\mathbf{R}\) の直交性を何らかの方法で確保しつつ解く必要があります。
この問題を回避する方法の1つとして、回転行列の代わりにオイラー角を未知変数とする方法があります。オイラー角の記事で示したように、オイラー角の時間微分と角速度ベクトルには次式の関係があります。
$$
\begin{bmatrix}
\dot{\psi} \\
\dot{\theta} \\
\dot{\phi}
\end{bmatrix}
=
\begin{bmatrix}
0 & \frac{\sin{\phi}}{\cos{\theta}} & \frac{\cos{\phi}}{\cos{\theta}} \\
0 & \cos{\phi} & -\sin{\phi} \\
1 & \frac{\sin{\phi}\sin{\theta}}{\cos{\theta}} & \frac{\cos{\phi}\sin{\theta}}{\cos{\theta}}
\end{bmatrix}
\boldsymbol{\omega}^\prime \tag{4}
$$
式(2)と(4)の常微分方程式を並列で解けば、独楽の角速度ベクトル \(\boldsymbol{\omega}^\prime\) とオイラー角 \((\psi, \theta, \phi)\) の時刻歴を求めることができます。また、式(1)を用いれば、各瞬間のオイラー角から回転行列を求めることができます。この場合、回転行列の直交性は保証されます。ただし、前項でも述べたように、オイラー角を用いる場合には、特異姿勢近傍での計算に注意が必要です。一長一短ですね。
では次に、式(3)に含まれている、独楽の支点周りの慣性行列 \(\mathbf{I}^\prime\) と、独楽に働く力のモーメント \(\mathbf{M}^\prime\) をそれぞれ具体的に求めてみましょう。
支点周りの慣性行列
座標系 \(O-x^{\prime}y^{\prime}z^{\prime}\) を平行移動し、原点を重心に一致させた座標系を \(G-x^{\prime\prime}y^{\prime\prime}z^{\prime\prime}\) とします。
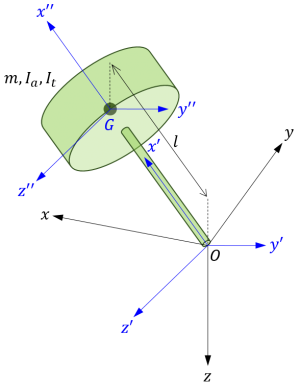
座標系 \(G-x^{\prime\prime}y^{\prime\prime}z^{\prime\prime}\) による独楽の慣性行列は、定義より
$$
\mathbf{I}^{\prime\prime} =
\begin{bmatrix}
I_a & 0 & 0\\
0 & I_t & 0\\
0 & 0 & I_t\\
\end{bmatrix} \tag{5}
$$
です。また、重心 \(G\) の位置ベクトル \(\vec{OG}\) の座標系 \(O-x^{\prime}y^{\prime}z^{\prime}\) による成分表示を \(\mathbf{r}_G^\prime\) とすると
$$
\mathbf{r}_G^\prime =
\begin{bmatrix}
l \\ 0 \\ 0\\
\end{bmatrix} \tag{6}
$$
です。
慣性行列の並進変換の公式(平行軸の定理)と式(5)(6)より、座標系 \(O-x^{\prime}y^{\prime}z^{\prime}\) による独楽の慣性行列は次のように求められます。
$$
\mathbf{I}^\prime = \mathbf{I}^{\prime\prime}-m\tilde{\mathbf{r}}_G^\prime\tilde{\mathbf{r}}_G^\prime =
\begin{bmatrix}
I_a & 0 & 0\\
0 & I_t+ml^2 & 0 \\
0 & 0 & I_t+ml^2 \\
\end{bmatrix} \tag{7}
$$
重力のモーメント
独楽に働く重力は、下図のように、重心に働く下向きの力 \(mg\) で表すことができます。
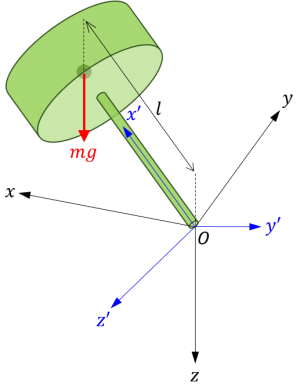
すなわち、独楽に働く重力ベクトルの座標系 \(O-xyz\) による成分表示は
$$ \mathbf{F}_g = \begin{bmatrix} 0 \\ 0 \\ mg \end{bmatrix} \tag{8}$$
です。このベクトルの座標系 \(O-x^{\prime}y^{\prime}z^{\prime}\) による成分表示は回転行列 \(\mathbf{R}\) を用いて
$$ \mathbf{F}_g^\prime = \mathbf{R}^T \mathbf{F}_g \tag{9}$$
と表せます。
独楽に働く支点 \(O\) 周りの重力のモーメントは、式(6)(8)(9)を用いて、次式により計算することができます。
$$ \mathbf{M}_g^\prime = \mathbf{r}_G^\prime \times \mathbf{F}_g^\prime = \tilde{\mathbf{r}}_G^\prime \mathbf{R}^T \mathbf{F}_g \tag{10} $$
シミュレーション
独楽のシミュレーション(動力学解析)では、式(2)と(3)または式(2)と(4)の常微分方程式を特定の初期条件の下で数値的に解き(時間積分し)、独楽の角速度 \(\boldsymbol{\omega}^\prime\) と回転行列 \(\mathbf{R}\) またはオイラー角 \((\psi,\theta,\phi)\) の時刻歴を求めます。
常微分方程式を数値的に解くためには、常微分方程式(ODE)ソルバーを用います。常微分方程式ソルバーとは、常微分方程式の数値計算アルゴリズムが実装されたソフトウェアのことで、様々なシミュレーションツールやプログラミング言語のライブラリで提供されています。
一般に、常微分方程式ソルバーは、次のような形式の初期値問題を解くように設計されています。
$$
\begin{cases}
\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x},t) \\
\mathbf{x}(t_0)=\mathbf{x}_0
\end{cases} \tag{11}
$$
ここで、\(\mathbf{x}\equiv\begin{bmatrix}x_1 & x_2 & \cdots x_n\end{bmatrix}^T\) は未知変数の列ベクトル、\(\mathbf{f}\equiv\begin{bmatrix}f_1(\mathbf{x}, t) & f_2(\mathbf{x}, t) & \cdots & f_n(\mathbf{x}, t)\end{bmatrix}^T\) は変数 \(\mathbf{x}\) と時間 \(t\) の関数の列ベクトル、\(t_0\) は初期時刻、\(\mathbf{x}_0\) は変数 \(\mathbf{x}\) の初期値です。
独楽のシミュレーションを行うために、式(2)と(4)を式(11)の形式で書くと次のようになります。
$$
\begin{cases}
\begin{bmatrix}
\dot{\mathbf{a}} \\
\dot{\boldsymbol{\omega}}^{\prime} \\
\end{bmatrix}
=
\begin{bmatrix}
\mathbf{G}(\mathbf{a})\boldsymbol{\omega}^\prime \\
{\mathbf{I}^{\prime}}^{-1}\left(\mathbf{M}^\prime(\mathbf{a}) – \tilde{\boldsymbol{\omega}^\prime}\mathbf{I}^{\prime}\boldsymbol{\omega}^\prime\right) \\
\end{bmatrix} \\
\begin{bmatrix}
\mathbf{a}(t_0) \\
\boldsymbol{\omega}^{\prime}(t_0) \\
\end{bmatrix}
=
\begin{bmatrix}
\mathbf{a}_0 \\
\boldsymbol{\omega}^{\prime}_0 \\
\end{bmatrix} \\
\end{cases} \tag{12}
$$
ここで、\(\mathbf{a}\equiv\begin{bmatrix}\psi & \theta & \phi\end{bmatrix}^T\) はオイラー角の列ベクトル、\(\mathbf{G}\) は式(4)右辺の係数行列、\(\mathbf{a}_0\) と \(\boldsymbol{\omega}^{\prime}_0\) はそれぞれオイラー角と角速度ベクトルの初期値を表します。
Scilab用シミュレーションプログラム
ここでは、Scilab を利用して、独楽の運動シミュレーションを実行する方法を紹介します。Scilab は無償で利用できるオープンソースの数値計算ソフトウェアです。
まずは、下記のような関数定義スクリプトを作成して「top.sci」という名前のファイルに保存します。このスクリプトでは、式(12)の独楽の常微分方程式を「top」という関数に定義しています。
// top.sci
/******************************************************************************
* 独楽(こま)の常微分方程式関数の定義
******************************************************************************/
// 独楽の常微分方程式関数
function [x_dot, request] = top(t, x)
// パラメータ
m = 1; // [kg] 質量
Ia = 0.02; // [kg*m^2] 対称軸周りの慣性モーメント
It = 0.01; // [kg*m^2] 重心を通り対称軸に直角な軸周りの慣性モーメント
l = 0.1; // [m] 重心と支点の距離
g = 9.8; // [m/s^2] 重力加速度
// 重心位置(剛体枠参照)
rG = [l; 0; 0];
// 支点周りの慣性行列(剛体枠参照)
I = diag([Ia, It, It]) - m*tilde(rG)*tilde(rG);
// オイラー角
psi = x(1); // [rad] 方位角
theta = x(2); // [rad] 傾角
phi = x(3); // [rad] 回転角
// 角速度ベクトル(剛体枠参照)
w = [x(4); x(5); x(6)];
// 三角関数値
S_psi = sin(psi);
S_theta = sin(theta);
S_phi = sin(phi);
C_psi = cos(psi);
C_theta = cos(theta);
C_phi = cos(phi);
// 回転行列
R = [
C_psi*C_theta, C_psi*S_theta*S_phi - C_phi*S_psi, S_psi*S_phi + C_psi*C_phi*S_theta;
C_theta*S_psi, C_psi*C_phi + S_psi*S_theta*S_phi, C_phi*S_psi*S_theta - C_psi*S_phi;
-S_theta, C_theta*S_phi, C_theta*C_phi];
// 重力モーメント(剛体枠参照)
M = tilde(rG)*R'*[0; 0; m*g];
// 角速度ベクトルの時間微分(オイラーの運動方程式、剛体枠参照)
w_dot = I\(M - tilde(w)*I*w);
// オイラー角の時間微分
a_dot = [
0, S_phi/C_theta, C_phi/C_theta;
0, C_phi, -S_phi;
1, S_phi*S_theta/C_theta, C_phi*S_theta/C_theta]*w;
// 状態ベクトルの時間微分
x_dot = [a_dot; w_dot];
// リクエスト変数
if argn(1) > 1
request.rG_inr = R*rG; // 重心の位置ベクトル(慣性枠参照)
end
endfunction
// チルダオペレータ
function a_tilde = tilde(a)
a_tilde = [
0, -a(3), a(2);
a(3), 0, -a(1);
-a(2), a(1), 0];
endfunction
次に、下記のようなシミュレーション実行スクリプトを作成し、「simulate_top.sce」という名前のファイルに保存します。このスクリプトを Scilab で実行すれば、シミュレーションが実行され、シミュレーション結果のプロットが表示されます。
// simulate_top.sce
/******************************************************************************
* 独楽(こま)の動力学シミュレーションを実行する
******************************************************************************/
clear; // ワークスペース変数をクリア
for i=winsid(), close(scf(i)), end; // 全ての図を閉じる
exec('top.sci'); // 独楽の常微分方程式関数を読み込み
// 初期条件の設定
psi_0 = 0; // [rad] 方位角
theta_0 = %pi/4; // [rad] 傾角
phi_0 = 0; // [rad] 回転角
wx_0 = 10*%pi; // [rad/s] x'軸周り角速度
wy_0 = 0; // [rad/s] y'軸周り角速度
wz_0 = 0; // [rad/s] z'軸周り角速度
x0 = [psi_0; theta_0; phi_0; wx_0; wy_0; wz_0]; // 状態ベクトルの初期値
// シミュレーション時間の設定
t0 = 0; // [s] 開始
tf = 5; // [s] 終了
dt = 0.01; // [s] 出力サンプル時間
t = t0:dt:tf; // [s] 出力時間ベクトル
// 常微分方程式ソルバーの実行
x = ode(x0, t0, t, top); // topは独楽の常微分方程式関数
// シミュレーション結果
nt = length(t); // 出力データ点数
psi = x(1,:); // [rad] 方位角
theta = x(2,:); // [rad] 傾角
phi = x(3,:); // [rad] 回転角
wx = x(4,:); // [rad/s] x'軸周り角速度
wy = x(5,:); // [rad/s] y'軸周り角速度
wz = x(6,:); // [rad/s] z'軸周り角速度
// リクエスト変数の初期化
rG_inr = zeros(3,nt); // 重心の位置ベクトル(慣性座標系参照)
// リクエスト変数の評価
for i = 1:nt
[x_dot, request] = top(t(i), x(:,i));
rG_inr(:,i) = request.rG_inr; // [m] 重心の位置ベクトル(慣性座標系参照)
end
// プロット設定
thickness = 2;
font_size = 3;
// オイラー角の時系列プロット
figure('figure_size', [626,700], 'background', -2);
margin_left = 0.16;
subplot(3,1,1);
plot(t, psi*180/%pi, 'thickness', thickness);
margins = gca().margins;
margins(1) = margin_left;
set(gca(), 'font_size', font_size, 'margins', margins);
ylabel('$\text{方位角}\\ \psi \text{ [deg]}$', 'font_size', font_size);
xgrid;
subplot(3,1,2);
plot(t, theta*180/%pi, 'thickness', thickness);
margins = gca().margins;
margins(1) = margin_left;
set(gca(), 'font_size', font_size, 'margins', margins);
ylabel('$\text{傾角}\\ \theta \text{ [deg]}$', 'font_size', font_size);
xgrid;
subplot(3,1,3);
plot(t, phi*180/%pi, 'thickness', thickness);
margins = gca().margins;
margins(1) = margin_left;
set(gca(), 'font_size', font_size, 'margins', margins);
ylabel('$\text{回転角}\\ \phi \text{ [deg]}$', 'font_size', font_size);
xgrid;
// 重心の軌跡プロット
figure('background', -2);
param3d(rG_inr(1,:), rG_inr(2,:), rG_inr(3,:));
set(gce(), 'thickness', thickness, 'foreground', 2);
title('重心の軌跡');
data_bounds = gca().data_bounds;
data_bounds(1,3) = -0.1;
data_bounds(2,3) = 0;
set(gca(), 'data_bounds', data_bounds, 'axes_reverse', ["off","on","on"],..
'rotation_angles', [72.5,131.5], 'font_size', font_size);
xgrid;
プログラム中の「パラメータ」や「初期条件の設定」変更すれば、色々な条件で独楽の運動をシミュレーションすることができます。ただし、オイラー角が特異姿勢近傍の値を取らないように注意します。
シミュレーション結果
上記のプログラムを実行して得られたシミュレーション結果のプロットを以下に示します。
- オイラー角の時系列プロット
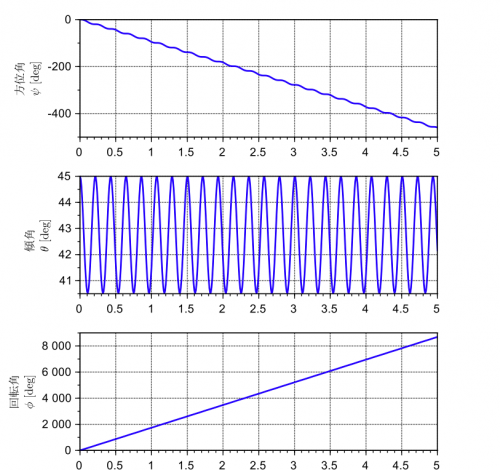
- 重心の軌跡プロット
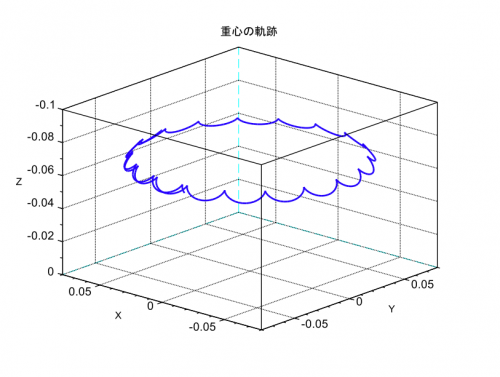
上記のプログラムには含まれていませんが、シミュレーション結果を下図のようなアニメーションで可視化すれば、独楽の運動をより直感的に把握することができます。
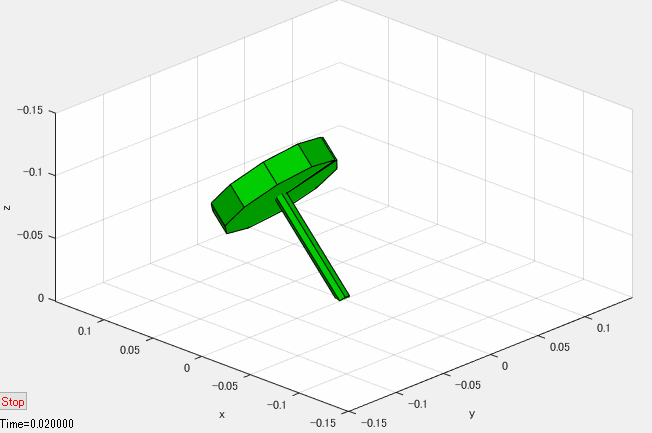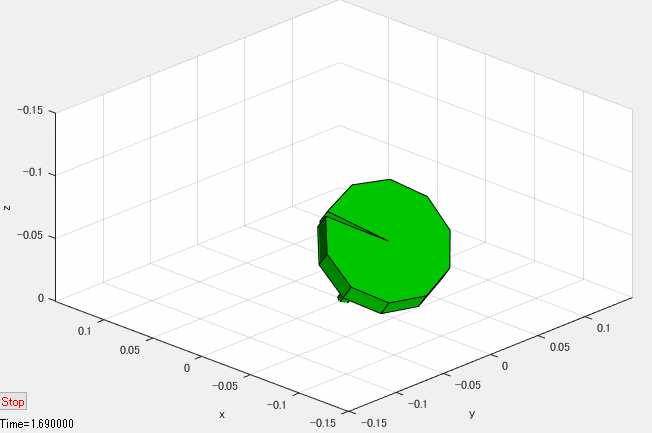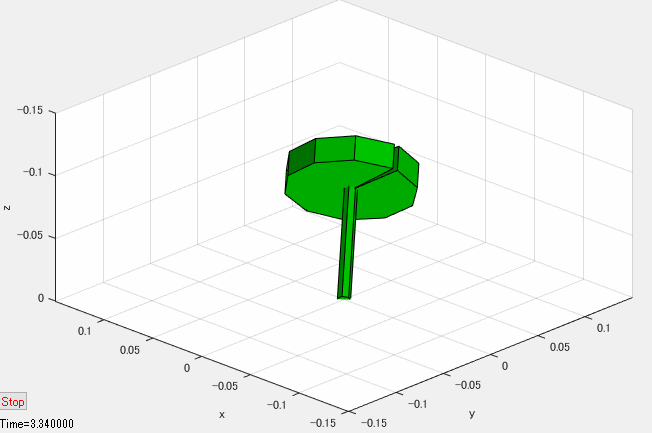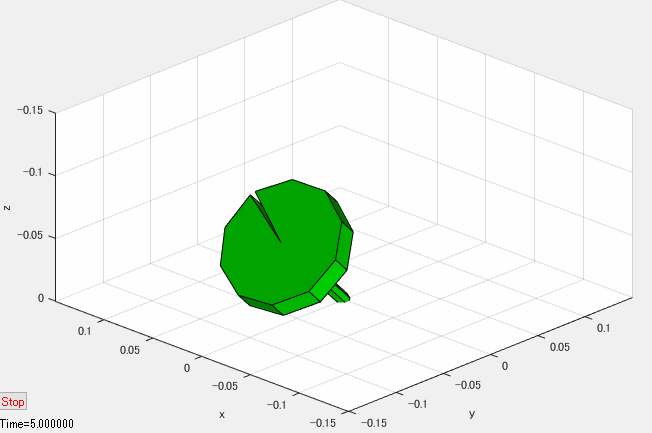
独楽の対称軸が垂直軸周りに振れ回る運動は歳差運動(precession)と呼ばれています。また、対称軸の傾角の振動は章動(nutation)と呼ばれています。初期条件や独楽のパラメータを変えたときに、歳差運動や章動がどのように変わるのか、シミュレーションで実験し、考察してみると面白いと思います。
まとめ
この記事では、独楽(こま)を例として、剛体の回転運動をシミュレーションする方法を解説しました。基本的には、オイラーの運動方程式と回転姿勢に関する微分方程式を連立し、常微分方程式ソルバーで解くという処理になりますが、問題に応じて適切な慣性行列と力のモーメントをオイラーの運動方程式に代入してやる必要があります。また、座標系の定め方が問題の複雑さに影響するので、座標系はよく吟味して適切に定める必要があります。
シミュレーションの利点の1つは手軽に実験ができることです。例えば、独楽の歳差運動や章動を数学的に解析しようとすると、かなりの数学テクニックが必要となりますが[1]、シミュレーションを用いて、初期値やパラメータを色々と変えて実験をしてみることで、数式と格闘しなくてもある程度の定量的な性質を掴むことができます。
最後まで読んでいただきありがとうございました。この記事がご参考になれば幸いです。
参考文献
[1] Greenwood, D.T. Principles of Dynamics. 2nd edition, Prentice Hall, 1988.







コメント