力や速度など、大きさだけでなく向きも問題となる量はベクトルと呼ばれます。ベクトルは図としては矢印で表示できますが、計算などでベクトルを代数的または数値的に扱いたい場合には、ベクトルの成分表示を利用します。
ベクトルの成分表示
下図のように、ベクトル \(\vec{a}\) を成分表示する場合には、\(\vec{a}\) を平行移動して基準となる座標系 \(O-xyz\) の原点に始点が来るように置きます。このときの終点の座標 \((a_x, a_y, a_z)\) がベクトル \(\vec{a}\) の成分と呼ばれるものです。[1]
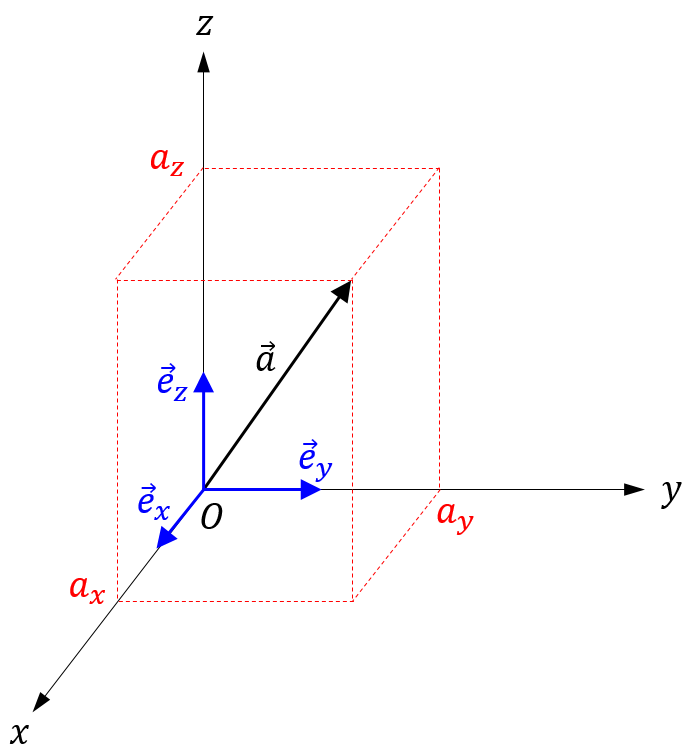
座標系の \(x\)軸、\(y\)軸、\(z\) 軸方向の単位ベクトル(大きさ1のベクトル)をそれぞれ \(\vec{e}_x\)、\(\vec{e}_y\)、\(\vec{e}_z\) とすれば、
$$\vec{a}=a_x\vec{e}_x+a_y\vec{e}_y+a_z\vec{e}_z$$
が成り立ちます。上式の右辺の各項は \(\vec{a}\) の成分ベクトルと呼ばれます。[1]
ベクトル \(\vec{a}\) の成分表示は、次のように成分を列行列にして表します。
$$\mathbf{a}=\begin{bmatrix} a_x \\ a_y \\ a_z \end{bmatrix}$$
\(\vec{a}\) を幾何ベクトル、\(\mathbf{a}\) を代数ベクトルと呼ぶこともあります。[2]
ベクトル成分表示の演算
任意のベクトル \(\vec{a}\)、\(\vec{b}\) の成分表示をそれぞれ \(\mathbf{a}\)、\(\mathbf{b}\) とすると、幾何ベクトルの演算は、以下のように代数ベクトルの演算に置き換えられます。[2]
- 和: \(\vec{a}+\vec{b} \quad \longrightarrow \quad \mathbf{a}+\mathbf{b}\)
- 内積: \(\vec{a}\cdot\vec{b} \quad \longrightarrow \quad \mathbf{a}\cdot\mathbf{b} \equiv \mathbf{a}^T\mathbf{b}\)
- 絶対値: \(|\vec{a}| \quad \longrightarrow \quad |\mathbf{a}| \equiv \sqrt{\mathbf{a}^T\mathbf{a}}\)
- 外積: \(\vec{a}\times\vec{b} \quad \longrightarrow \quad \mathbf{a}\times\mathbf{b}\equiv\tilde{\mathbf{a}}\mathbf{b}\)
ここで、上付きの \(T\) は行列の転置を表し、\(\tilde{\mathbf{a}}\) は \(\mathbf{a}\) のチルダ行列と呼ばれる歪対称行列で次のように定義されます。
$$\mathbf{a}=\begin{bmatrix} a_x \\ a_y \\ a_z \end{bmatrix} \quad \Rightarrow \quad \tilde{\mathbf{a}}=\begin{bmatrix} 0 & -a_z & a_y \\ a_z & 0 & -a_x \\ -a_y & a_x & 0 \end{bmatrix}$$
記号「\(\tilde{}\)」を、代数ベクトルからチルダ行列を作る演算子とみなし、チルダオペレータ(外積オペレータ)と呼ぶこともあります。
代数ベクトルの演算は、通常の行列演算則に従って行うことができます。
ベクトル成分表示の座標変換
ベクトルの成分表示は座標系に依存します。下図のように、座標系 \(O-xyz\) と平行でない座標系 \(O^{\prime}-x^{\prime}y^{\prime}z^{\prime}\) を考えます。(一般性を失うことなく、原点 \(O\) と \(O^\prime\) が一致したケースで考えることができます。)
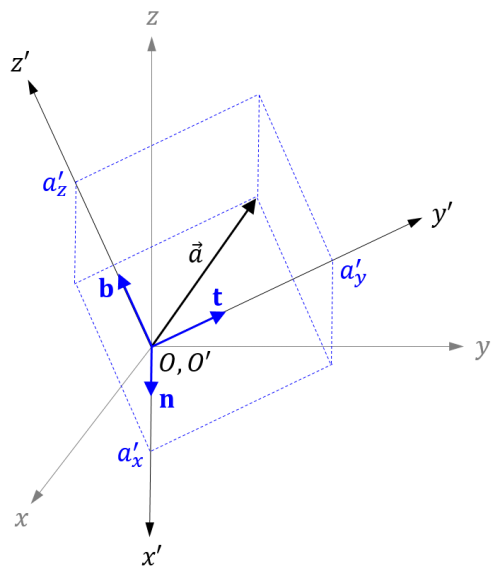
ベクトル \(\vec{a}\) の座標系 \(O-xyz\) と座標系 \(O^{\prime}-x^{\prime}y^{\prime}z^{\prime}\) による成分表示をそれぞれ
$$\mathbf{a}=\begin{bmatrix} a_x \\ a_y \\ a_z \end{bmatrix}, \quad \mathbf{a}^\prime=\begin{bmatrix} a_x^\prime \\ a_y^\prime \\ a_z^\prime \end{bmatrix}$$
とすると、一般に \(\mathbf{a}\ne\mathbf{a}^\prime\) です。
では、\(\mathbf{a}\) と \(\mathbf{a}^\prime\) の関係はどのように記述できるでしょうか。
上図に示されているように、\(x^\prime\)軸、\(y^\prime\)軸、\(z^\prime\)軸方向の単位ベクトルの座標系 \(O-xyz\) による成分表示をそれぞれ \(\mathbf{n}\)、\(\mathbf{t}\)、\(\mathbf{b}\) とすると、次の関係式が成り立ちます。
$$\begin{align} \mathbf{a} &= a_x^\prime\mathbf{n}+a_y^\prime\mathbf{t}+a_z^\prime\mathbf{b} \\ &= \begin{bmatrix} \mathbf{n} & \mathbf{t} & \mathbf{b} \end{bmatrix}\begin{bmatrix} a_x^\prime \\ a_y^\prime \\ a_z^\prime \end{bmatrix} \end{align}$$
ここで、
$$\mathbf{R}=\begin{bmatrix} \mathbf{n} & \mathbf{t} & \mathbf{b} \end{bmatrix}$$
と置くと
$$\mathbf{a}=\mathbf{R}\mathbf{a}^\prime \tag{1}$$
を得ます。行列 \(\mathbf{R}\) は座標系 \(O-xyz\) に対する座標系 \(O^{\prime}-x^{\prime}y^{\prime}z^{\prime}\) の回転行列(または方向余弦行列)と呼ばれるものです。すなわち、回転行列を用いれば、ベクトルのある座標系による成分表示を別の座標系による成分表示に変換できるというわけです。[3]
回転行列は正規直交性という性質を持っており
$$\mathbf{R}^T=\mathbf{R}^{-1} \tag{2}$$
を満たすため、式(1)と(2)より、次の逆変換の関係も得られます。
$$\mathbf{a}^\prime=\mathbf{R}^T\mathbf{a}$$
行列 \(\mathbf{R}\) と \(\mathbf{R}^T\) は座標変換行列とも呼ばれます。[2][3]
回転行列については、以下の記事で詳しく解説していますのでよろしければご覧ください。
チルダ行列の座標変換
最後に、力学ではベクトルの外積がよく出てきますが、外積を含む式の操作で良く利用される、チルダ行列の座標変換について記しておきたいと思います。
2つの座標系 \(O-xyz\) と \(O^{\prime}-x^{\prime}y^{\prime}z^{\prime}\) を考え、前者に対する後者の回転行列を \(\mathbf{R}\) とします。任意のベクトル \(\vec{\omega}\) の各座標系による成分表示をそれぞれ \(\boldsymbol{\omega}\)、\(\boldsymbol{\omega}^\prime\) とすると、式(1)より、
$$ \boldsymbol{\omega} = \mathbf{R}\boldsymbol{\omega}^\prime \tag{3} $$
が成り立ちます。
ここで調べたいのは、\(\boldsymbol{\omega}\) と \(\boldsymbol{\omega}^\prime\) のチルダ行列 \(\tilde{\boldsymbol{\omega}}\) と \(\tilde{\boldsymbol{\omega}^\prime}\) の関係です。
式(3)を分解すると、
$$ \boldsymbol{\omega} = \begin{bmatrix} \mathbf{n} & \mathbf{t} & \mathbf{b} \end{bmatrix} \begin{bmatrix} \omega_x^\prime \\ \omega_y^\prime \\ \omega_y^\prime \end{bmatrix} = \omega_x^\prime\mathbf{n} + \omega_y^\prime\mathbf{t} + \omega_z^\prime\mathbf{b} $$
この両辺のチルダ行列を取ると、チルダオペレータは分配法則が成り立つので、
$$ \tilde{\boldsymbol{\omega}} = \omega_x^\prime\tilde{\mathbf{n}} + \omega_y^\prime\tilde{\mathbf{t}} + \omega_z^\prime\tilde{\mathbf{b}} \tag{4}$$
を得ます。式(4)の両辺に右から \(\mathbf{n}\) を掛けると、\(\mathbf{n}, \mathbf{t}, \mathbf{b}\) はそれぞれ座標軸方向の単位ベクトルなので、
$$
\begin{align}
\tilde{\boldsymbol{\omega}}\mathbf{n} & = \omega_x^\prime\tilde{\mathbf{n}}\mathbf{n} + \omega_y^\prime\tilde{\mathbf{t}}\mathbf{n} + \omega_z^\prime\tilde{\mathbf{b}}\mathbf{n} \\
& = \omega_x^\prime(\mathbf{n}\times\mathbf{n}) + \omega_y^\prime(\mathbf{t}\times\mathbf{n}) + \omega_z^\prime(\mathbf{b}\times\mathbf{n}) \\
& = -\omega_y^\prime\mathbf{b} + \omega_z^\prime\mathbf{t} \\
& = \underbrace{\begin{bmatrix} \mathbf{n} & \mathbf{t} & \mathbf{b} \end{bmatrix}}_{\mathbf{R}} \begin{bmatrix} 0 \\ \omega_z^\prime \\ -\omega_y^\prime \end{bmatrix} \tag{5}
\end{align}
$$
同様に、式(4)の両辺に右から \(\mathbf{t}\)、\(\mathbf{b}\) を掛けると
$$
\tilde{\boldsymbol{\omega}}\mathbf{t} = \mathbf{R}\begin{bmatrix} -\omega_z^\prime \\ 0 \\ \omega_x^\prime \end{bmatrix} \tag{6}
$$
$$
\tilde{\boldsymbol{\omega}}\mathbf{b} = \mathbf{R}\begin{bmatrix} \omega_y^\prime \\ -\omega_x^\prime \\ 0 \end{bmatrix} \tag{7}
$$
を得ます。式(5)(6)(7)をまとめると、
$$
\tilde{\boldsymbol{\omega}}\begin{bmatrix} \mathbf{n} & \mathbf{t} & \mathbf{b} \end{bmatrix} =
\mathbf{R}
\begin{bmatrix}
0 & -\omega_z^\prime & \omega_y^\prime \\
\omega_z^\prime & 0 & -\omega_x^\prime \\
-\omega_y^\prime & \omega_x^\prime & 0
\end{bmatrix}
$$
つまり、
$$ \tilde{\boldsymbol{\omega}}\mathbf{R} = \mathbf{R}\tilde{\boldsymbol{\omega}^\prime} \tag{8} $$
となります。また、式(8)の両辺に右から \(\mathbf{R}^T\)を掛けて(2)の性質を用いると、
$$ \tilde{\boldsymbol{\omega}} = \mathbf{R}\tilde{\boldsymbol{\omega}^\prime}\mathbf{R}^T \tag{9} $$
を得ます。また、式(3)を(9)へ代入して、式(9)の代わりに次のように書くこともできます。
$$
\widetilde{\mathbf{R}\boldsymbol{\omega}^\prime} = \mathbf{R}\tilde{\boldsymbol{\omega}^\prime}\mathbf{R}^T \tag{10}
$$
式(8)(9)または(10)は便利な公式としてよく利用されます。
【補足】
より簡潔には、
$$ \boldsymbol{\omega}\times\mathbf{r}=\mathbf{R}(\boldsymbol{\omega}^{\prime}\times\mathbf{r}^{\prime}) $$
の関係から
$$ \tilde{\boldsymbol{\omega}}\mathbf{r} = \mathbf{R}\tilde{\boldsymbol{\omega}^{\prime}}\mathbf{r}^{\prime} = \mathbf{R}\tilde{\boldsymbol{\omega}^{\prime}}\mathbf{R}^T\mathbf{r} $$
が得られ、両辺の \(\mathbf{r}\) の係数行列を比較すれば、式(9)が求められます。
参考文献
[1] Spiegel, M. R; Liu, J. Mathematical Handbook of Formulas and Tables, 2nd edition, Schaum’s Outline Series, McGraw-Hill, 1999.
[2] 日本機械学会編. マルチボディダイナミクス(1)基礎理論, コンピュータダイナミクスシリーズ3, コロナ社, 2006.
[3] Asada, H.; Slotine, J.-J. E. Robot Analysis and Control, John Wiley & Sons, 1986.






コメント
[…] […]