剛体の慣性モーメント・慣性行列（慣性テンソル）とは？定義・物理的意味・公式・定理のまとめ

剛体の回転運動を計算する際には、慣性モーメントや慣性行列（慣性テンソル）と呼ばれる量が必要となります。前回の記事では、剛体の回転運動を支配するオイラーの運動方程式の導出について解説し、慣性行列についても少し触れました。この記事では、あらためて慣性モーメントと慣性行列（慣性テンソル）について少し掘り下げて解説しつつ、それらの定義と物理的な意味、また関連する重要な公式や定理をまとめてみます。

慣性モーメント

定義

まずは、１つの軸周りの慣性モーメントの定義から始めましょう。

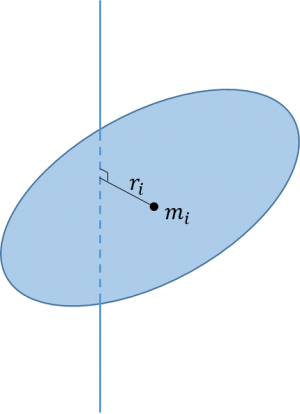
上図のように、剛体に対して１つの軸を定めたとき、次式で定義される量をその軸周りの慣性モーメント（moment of inertia）と呼びます。[1]

$$ I = \sum_{i} m_{i} r_{i}^2 \tag{1}$$

ここで、剛体は質量 \(m_1, m_2, … \) の質点の集まりで構成されているとし、\(r_{i}\) は質点 \(m_{i}\) と軸の距離です。

質量が連続的に分布している場合には、慣性モーメントは次式のような体積積分になります。[1]

$$ I = \int_{V} \rho r^2 dV \tag{2}$$

ここで、\(V\) は剛体の体積、\(\rho\) は質量密度、\(r\) は微小体積 \(dV\) と軸の距離です。

式(1)や(2)から、質量が軸から離れて多く分布しているほど、慣性モーメントは大きくなることが分かります。

例１（離散的な質量分布）

質量 \(m\) の質点４つで構成される剛体が、下図のように配置されているとします。

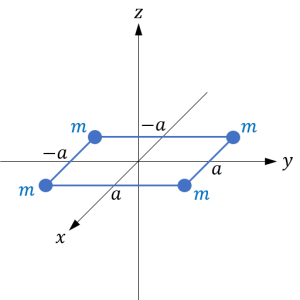
このとき、剛体の \(z\) 軸周りの慣性モーメントは

$$ I_z = 4\times m (2a^2) = 8ma^2 $$

\(x\) 軸周りおよび \(y\) 軸周りの慣性モーメントは

$$ I_x = I_y = 4\times m a^2 = 4ma^2 $$

となります。

例２（連続的な質量分布）

下図のような、半径 \(a\)、高さ \(h\) 、一定密度 \(\rho\) の円柱の剛体を考えます。

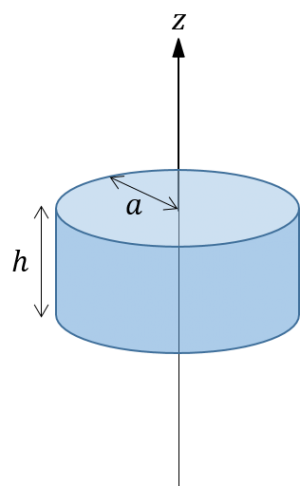
円筒座標を \((r, \theta, z)\) とすれば、円柱の中心軸（ \(z\) 軸）周りの慣性モーメントは以下のように計算できます。

$$
\begin{align}
I & = \underbrace{\int_{r=0}^{a}\int_{\theta=0}^{2\pi}\int_{z=-\frac{h}{2}}^{\frac{h}{2}}}_{\int_{V}} \rho r^2 \underbrace{(dr)(r d\theta)(dz)}_{dV} \\
& = \rho\int_{r=0}^{a} r^3 dr \int_{\theta=0}^{2\pi} d\theta \int_{z=-\frac{h}{2}}^{\frac{h}{2}} dz \\
& = \rho \left(\frac{a^4}{4}\right) (2\pi) h \\
& = \frac{\rho\pi a^4 h}{2} \\
& = \frac{ma^2}{2} \\
\end{align}
$$

ここで、\(m=\rho \pi a^2 h\) は円柱剛体の質量です。

種々の形状の慣性モーメント

上の例２では円柱剛体の慣性モーメントを定義式から計算しましたが、種々の形状の慣性モーメントは多くの教科書や便覧にまとめられています。必要な場合にはそれらを参照すれば、計算する手間が省けます。

慣性モーメントの物理的意味

慣性モーメントの物理的な意味を考えてみましょう。

下図のように、剛体が一つの固定軸周りにのみ回転できるとします。

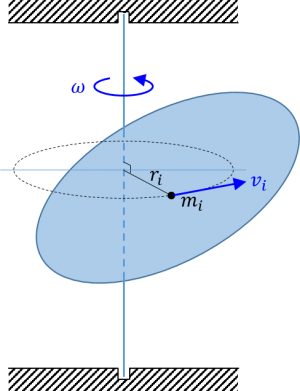
剛体が固定軸周りに回転するとき、剛体中の各質点は半径 \(r_i\) の円運動をしますから、剛体の角速度（回転角の時間微分）を \(\omega\) とすれば、各質点の速度は \(v_i = r_i \omega\) です。

各質点の固定軸周りの角運動量は

$$ h_i = r_i\times m_i v_i = m_i r_i^2 \omega $$

ですから、剛体の固定軸周りの角運動量は各質点の角運動量を足し合わせて

$$ H = \sum_i h_i = \sum_i m_i r_i^2 \omega = I\omega \tag{3}$$

となります。ここで \(I\) は剛体の固定軸周りの慣性モーメント（式(1)）です。

また、各質点の運動エネルギーは

$$ \tau_i = \frac{1}{2}m_i v_i^2 = \frac{1}{2}m_i r_i^2 \omega^2 $$

ですから、剛体の運動エネルギーは各質点の運動エネルギーを足し合わせて

$$ T = \sum_i \tau_i = \frac{1}{2}\sum_i m_i r_i^2 \omega^2 = \frac{1}{2}I\omega^2 \tag{4}$$

となります。

固定軸と各質点の距離 \(r_i\) は剛体が回転しても変わりませんから、慣性モーメント \(I\) は剛体が回転しても一定です。剛体に働く固定軸周りの力のモーメントを \(M\) とすると、固定軸周りの角運動量 \(H\) の時間微分は \(M\) と等しくなりますから、式(3)を時間微分して、

$$ \dot{H} = I\dot{\omega} = M \tag{5}$$

を得ます。式(5)は固定軸をもつ剛体の回転運動方程式です。[1]

式(3)(4)(5)から、剛体の固定軸周りの回転運動は、剛体の質量分布を直接用いる代わりに、慣性モーメントを用いて記述できることが分かります。また、剛体の回転運動における慣性モーメントは、質点の並進運動における質量に相当する量であることが分かります。

慣性行列

前項で示したように、剛体の固定軸周りの回転運動はその軸周りの慣性モーメントを用いて記述することができます。一方、剛体の任意の回転運動を記述する場合には、慣性行列（慣性テンソル）と呼ばれる量が必要となります。

この項以降では、次の関連記事で説明している概念や結果を利用しますので、必要に応じて参照してください。

定義

下図のように、剛体と任意の座標系 \(O-xyz\) を考えます。

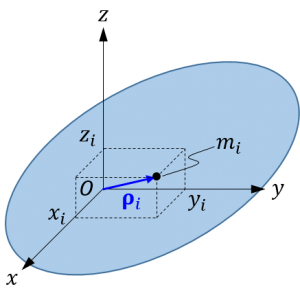
質点 \(m_i\) の位置ベクトルの成分表示を \(\boldsymbol{\rho}_i = \begin{bmatrix}x_i & y_i & z_i\end{bmatrix}^T\) とすれば、慣性行列（inertia matrix）は次のように定義されます。[2][3]

$$
\begin{align}
\mathbf{I}
& \equiv
-\sum_{i} m_i \tilde{\boldsymbol{\rho}}_i \tilde{\boldsymbol{\rho}}_i \\
& =
-\sum_{i} m_i
\begin{bmatrix}
0 & -z_i & y_i \\
z_i & 0 & -x_i \\
-y_i & x_i & 0
\end{bmatrix}
\begin{bmatrix}
0 & -z_i & y_i \\
z_i & 0 & -x_i \\
-y_i & x_i & 0
\end{bmatrix} \\
& =
\sum_{i} m_i
\begin{bmatrix}
y_i^2+z_i^2 & -x_i y_i & -x_i z_i \\
-x_i y_i & x_i^2+z_i^2 & -y_i z_i \\
-x_i z_i & -y_i z_i & x_i^2+y_i^2
\end{bmatrix} \tag{6}\\
\end{align}
$$

ここで、\(\tilde{\boldsymbol{\rho}}_i\) は \(\boldsymbol{\rho}_i\) のチルダ行列（上記関連記事を参照）を表します。

連続的に質量が分布している剛体の場合、微小体積 \(dV\) の位置ベクトルの成分表示を \(\boldsymbol{\rho} = \begin{bmatrix}x & y & z\end{bmatrix}^T\) とすれば、慣性行列は次の体積積分になります。[2][3]

$$
\begin{align}
\mathbf{I}
& =
-\int_{V} \rho\tilde{\boldsymbol{\rho}}\tilde{\boldsymbol{\rho}} \: dV \\
& =
-\int_{V} \rho
\begin{bmatrix}
0 & -z & y \\
z & 0 & -x \\
-y & x & 0
\end{bmatrix}
\begin{bmatrix}
0 & -z & y \\
z & 0 & -x \\
-y & x & 0
\end{bmatrix}
dV \\
& =
\int_{V} \rho
\begin{bmatrix}
y^2+z^2 & -xy & -xz \\
-xy & x^2+z^2 & -yz \\
-xz & -yz & x^2+y^2
\end{bmatrix}
dV \tag{7}\\
\end{align}
$$

ここで、\(V\) は剛体の体積、\(\rho\) は質量密度です。

式(6)や(7)から、慣性行列 \(\mathbf{I}\) は \(\mathbf{I}^T=\mathbf{I}\) を満たす対称行列であることが分かります。慣性行列を

$$
\mathbf{I} =
\begin{bmatrix}
I_{xx} & I_{xy} & I_{xz} \\
I_{xy} & I_{yy} & I_{yz} \\
I_{xz} & I_{yz} & I_{zz} \\
\end{bmatrix} \tag{8}
$$

と書けば、対角項 \(I_{xx}, I_{yy}, I_{zz}\) はそれぞれ \(x, y, z\) 軸周りの慣性モーメントです。非対角項の \(I_{xy}, I_{xz}, I_{yz}\) は慣性乗積（product of inertia）と呼ばれます。[2][3]

慣性行列の座標変換

慣性行列は座標系に依存します。座標系を変えたときに、慣性行列がどのように変化するか見てみましょう。

並進変換（平行軸の定理）

下図のように、剛体と任意の座標系 \(O-xyz\) 、および剛体の重心 \(G\) を原点とし \(O-xyz\) と平行な座標系 \(G-x^{\prime}y^{\prime}z^{\prime}\) を考えます。

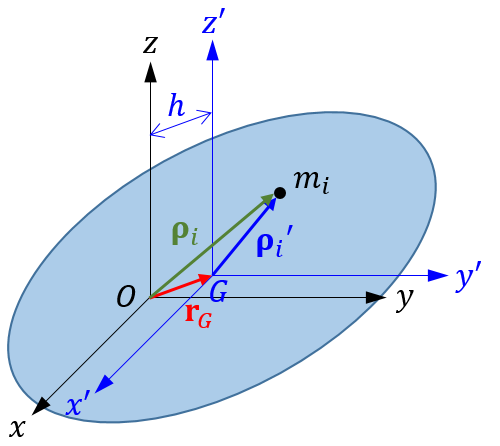
点 \(O\) と点 \(G\) に対する質点 \(m_i\) の位置ベクトルの成分表示をそれぞれ \(\boldsymbol{\rho}_i, \boldsymbol{\rho}_i^\prime\) 、点 \(O\) に対する点 \(G\) の位置ベクトルの成分表示を \(\mathbf{r}_{G}\) とすると、

$$ \boldsymbol{\rho}_i = \mathbf{r}_G + \boldsymbol{\rho}_i^\prime \tag{9}$$

の関係があります。式(9)の両辺のチルダ行列を取れば、

$$ \tilde{\boldsymbol{\rho}}_i = \tilde{\mathbf{r}}_G + \tilde{\boldsymbol{\rho}}_i^\prime \tag{10} $$

です。式(10)を式(1)に代入して展開すれば、

$$
\begin{align}
\mathbf{I}
& = -\sum_{i} m_i\tilde{\boldsymbol{\rho}}_i\tilde{\boldsymbol{\rho}}_i \\
& = -\sum_i m_i (\tilde{\mathbf{r}}_G + \tilde{\boldsymbol{\rho}}_i^\prime)(\tilde{\mathbf{r}}_G + \tilde{\boldsymbol{\rho}}_i^\prime) \\
& = -m\tilde{\mathbf{r}}_G \tilde{\mathbf{r}}_G – \left(\sum_i m_i \tilde{\boldsymbol{\rho}}_i^\prime\right) \tilde{\mathbf{r}}_G – \tilde{\mathbf{r}}_G \left(\sum_i m_i \tilde{\boldsymbol{\rho}}_i^\prime\right) \underbrace{- \sum_{i} m_i \tilde{\boldsymbol{\rho}_i^\prime} \tilde{\boldsymbol{\rho}_i^\prime}}_{\mathbf{I}^\prime} \\
\end{align}
$$

となります。ここで、\(\mathbf{I}\) は座標系 \(O-xyz\) による慣性行列、\(\mathbf{I}^\prime\) は座標系 \(G-x^{\prime}y^{\prime}z^{\prime}\) による慣性行列、\(m=\sum_i m_i\) は剛体の質量です。点 \(G\) は剛体の重心ですから、重心の定義より、上式右辺の第２項と第３項のカッコ内の和は \(0\) になります。従って、次の関係式が得られます。

$$ \mathbf{I} = \mathbf{I}^\prime – m\tilde{\mathbf{r}}_G \tilde{\mathbf{r}}_G \tag{11}$$

式(11)は、慣性行列の並進座標変換の式です。また、式(11)の両辺の \((3,3)\) 成分だけを抜き出せば、\(z\) 軸周りの慣性モーメント \(I_{zz}\) と \(z^\prime\) 軸周りの慣性モーメント \(I_{zz}^\prime\) を関連付ける次式が得られます。

$$ I_{zz} = I_{zz}^\prime + mh^2 \tag{12}$$

ここで、\(h\) は \(z\) 軸と \(z^\prime\) 軸の距離です（上図参照）。座標系 \(O-xyz\) は任意なので、式(12)の関係は、任意の軸と、それと平行で重心を通る軸について一般的に成り立ち、平行軸の定理（parallel-axis theorem）として知られています。[2]

回転変換

下図のように、剛体と任意の座標系 \(O-xyz\)、および座標系 \(O-xyz\) に対して傾いている座標系 \(O-x^{\prime} y^{\prime} z^{\prime}\) を考えます。

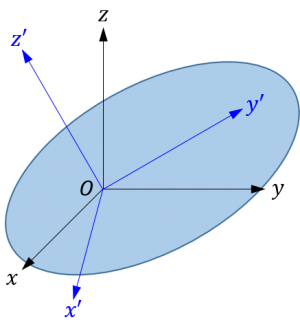
質点 \(m_i\) の位置ベクトル \(\vec{\rho}_i\) の座標系 \(O-xyz\) による成分表示を \(\boldsymbol{\rho}_i\)、座標系 \(O-x^{\prime} y^{\prime} z^{\prime}\) による成分表示を \(\boldsymbol{\rho}^\prime\)、座標系 \(O-xyz\) に対する座標系 \(O-x^{\prime} y^{\prime} z^{\prime}\) の回転行列（方向余弦行列）を \(\mathbf{R}\) とすれば、

$$ \boldsymbol{\rho}_i = \mathbf{R}\boldsymbol{\rho}_i^{\prime} \tag{13}$$

の関係があります。また、「ベクトルの成分表示と座標変換」の記事で示したように、式(13)の関係を持つ \(\boldsymbol{\rho}_i\) と \(\boldsymbol{\rho}_i^\prime\) のチルダ行列 \(\tilde{\boldsymbol{\rho}_i}\) と \(\tilde{\boldsymbol{\rho}_i^\prime}\) の間には次の関係があります。

$$
\tilde{\boldsymbol{\rho}_i} = \mathbf{R}\tilde{\boldsymbol{\rho}_i^\prime}\mathbf{R}^T \tag{14}
$$

式(14)を(1)に代入して、回転行列 \(\mathbf{R}\) が直交行列である（\(\mathbf{R}^{-1}=\mathbf{R}^T\) である）ことを考慮すれば、

$$
\begin{align}
\mathbf{I}
& =
-\sum_{i} m_i\tilde{\boldsymbol{\rho}}_i\tilde{\boldsymbol{\rho}}_i \\
& =
-\sum_{i} m_i
(\mathbf{R}\tilde{\boldsymbol{\rho}_i^\prime}\mathbf{R}^T)
(\mathbf{R}\tilde{\boldsymbol{\rho}_i^\prime}\mathbf{R}^T)  \\
& =
\mathbf{R}
\left[-\sum_{i} m_i\tilde{\boldsymbol{\rho}_i^\prime}\tilde{\boldsymbol{\rho}_i^\prime} \right]
\mathbf{R}^T \\
\end{align}
$$

つまり、

$$ \mathbf{I}=\mathbf{R} \mathbf{I}^\prime \mathbf{R}^T \tag{15}$$

の関係式を得ます。ここで、\(\mathbf{I}\) は座標系 \(O-xyz\) による慣性行列、\(\mathbf{I}^\prime\) は座標系 \(O-x^{\prime}y^{\prime}z^{\prime}\) による慣性行列です。式(15)は、慣性行列の回転座標変換の式です。また、式(15)の両辺に左から \(\mathbf{R}^T\)、右から \(\mathbf{R}\) を乗ずれば、逆変換の式

$$ \mathbf{I}^\prime=\mathbf{R}^T \mathbf{I} \mathbf{R} \tag{16}$$

が得られます。

慣性行列の物理的意味

任意の軸周りの慣性モーメント

式(16)の両辺に左から \(\begin{bmatrix}0 & 0 & 1\end{bmatrix}\)、右から \(\begin{bmatrix}0 & 0 & 1\end{bmatrix}^T\) を掛けると、\(\mathbf{I}^\prime\) の\((3,3)\) 成分である \(z^\prime\) 軸周りの慣性モーメントを取り出すことができます。

$$
\begin{align}
I_{zz}^\prime
& = \begin{bmatrix}0 & 0 & 1\end{bmatrix}\mathbf{R}^T \mathbf{I} \mathbf{R} \begin{bmatrix}0 \\ 0 \\ 1\end{bmatrix} \\
& = \mathbf{b}^T \mathbf{I} \mathbf{b} \tag{17}\\
\end{align}
$$

ここで、\(\mathbf{b}\) は \(\mathbf{R}\) の３列目の列ベクトルであり、\(z^\prime\) 軸方向単位ベクトルの座標系 \(O-xyz\) による成分表示です。

一般に、剛体の座標系 \(O-xyz\) による慣性行列が \(\mathbf{I}\) であるとき、原点 \(O\) を通り、単位方向ベクトルが \(\mathbf{e}\) の軸周りの慣性モーメントは次式で求められます。

$$ I = \mathbf{e}^T \mathbf{I} \mathbf{e} \tag{18}$$

つまり、慣性行列は座標系の原点を通るあらゆる軸周りの慣性モーメントの情報を含んでいることが分かります。

剛体の回転運動方程式

剛体の任意の回転運動は、慣性行列を用いて記述することができます。慣性行列を用いた剛体の回転運動方程式は、オイラーの運動方程式と呼ばれています。オイラーの運動方程式については、以下の関連記事で詳しく解説していますので、そちらを参照してください。

慣性主軸と主慣性モーメント

式(6)または(7)の定義より、慣性行列 \(\mathbf{I}\) は対称行列です。線形代数のスペクトル定理によれば、対称行列は直交変換により対角化することができます。すなわち、\(\mathbf{S}^T \mathbf{I} \mathbf{S}\) が対角行列になるような直交行列 \(\mathbf{S}\) が存在します。[4]

一方、式(16)による慣性行列の回転変換は直交変換ですので、スペクトル定理と組み合わせれば、式(16)の回転変換により \(\mathbf{I}^\prime\) が対角行列になるような回転行列 \(\mathbf{R}\) が存在するということになります。これはつまり、「慣性行列が対角行列になる座標系 \(O-x^{\prime}y^{\prime}z^{\prime}\) が存在する」ということです。

座標系 \(O-x^{\prime}y^{\prime}z^{\prime}\) による慣性行列 \(\mathbf{I}^\prime\) が対角行列になるとき、\(x^{\prime}\) 軸、\(y^{\prime}\) 軸、および \(z^{\prime}\) 軸は慣性主軸（principal axes of inertia）と呼ばれます。また、慣性主軸周りの慣性モーメントは主慣性モーメント（principal moment of inertia）と呼ばれます。[1][2]

慣性主軸と主慣性モーメントは、次の固有値問題を解くことにより求めることができます。[2]

$$ \mathbf{I}\mathbf{e}=I\mathbf{e} \tag{19}$$

固有値 \(I\) は主慣性モーメント、固有ベクトル \(\mathbf{e}\) は慣性主軸の方向ベクトルを与えます。

慣性楕円体

任意の座標系 \(O-xyz\) において、剛体の慣性行列 \(\mathbf{I}\) が与えられたとき、

$$ \boldsymbol{\rho}^T \mathbf{I}\boldsymbol{\rho}=1 \tag{20}$$

を満たす座標 \(\boldsymbol{\rho} \in \mathbb{R}^3\) の集合を考えます。

\(\mathbf{I}\) を式(8)で表し、\(\boldsymbol{\rho} = \begin{bmatrix}x & y & z\end{bmatrix}^T\) とすれば、式(20)は

$$
I_{xx}x^2 + I_{yy}y^2 + I_{zz}z^2 + 2I_{xy}xy + 2I_{xz}xz + 2I_{yz}yz = 1 \tag{21}
$$

と表すことができ、これは楕円体面の方程式です。この面を持つ楕円体を慣性楕円体（ellipsoid of inertia）と呼びます。[1][2]

式(20)と式(18)を比較すると、

$$ \boldsymbol{\rho} = \frac{\mathbf{e}}{\sqrt{I}} \tag{22}$$

の関係があります。ここで、\(\mathbf{e}\) は単位ベクトル、\(I\) は原点 \(O\) を通り \(\mathbf{e}\) と平行な軸の周りの慣性モーメントです。\(\boldsymbol{\rho} = \rho\mathbf{e}\) とすれば、式(22)より

$$ \rho = \frac{1}{\sqrt{I}} \tag{23}$$

または

$$ I = \frac{1}{\rho^2} \tag{24}$$

を得ます。式(24)が意味するところは、「原点 \(O\) と慣性楕円体面上の点を結ぶ線分の距離 \(\rho\) の2乗の逆数が、その線分周りの慣性モーメント \(I\) と等しくなる」ということです。（下図参照）

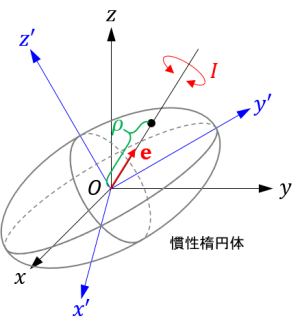
また、\(I\) は剛体に対する特性であり座標系に依りませんから、式(23) は、慣性楕円体が剛体に固定され、座標系に依らないことを示唆しています。

座標系 \(O-x^{\prime}y^{\prime}z^{\prime}\) を慣性主軸と一致するように取れば、この座標系による慣性楕円体面の方程式は

$$ I_{xx}^{\prime}{x^{\prime}}^2 + I_{yy}^{\prime}{y^{\prime}}^2 + I_{zz}^{\prime}{z^{\prime}}^2 = 1 \tag{25}$$

となります。ここで、\(I_{xx}^{\prime}, I_{yy}^{\prime}, I_{zz}^{\prime}\) は主慣性モーメントです。式(25)より、慣性楕円体の主軸半径は

$$ \rho_{x}=\frac{1}{\sqrt{I_{xx}^\prime}}, \quad \rho_{y}=\frac{1}{\sqrt{I_{yy}^\prime}}, \quad \rho_{z}=\frac{1}{\sqrt{I_{zz}^\prime}} \tag{26}$$

です。

一般に、楕円体の半径は主軸で極値を取りますから、式(23)(26)より、慣性モーメントも主軸周りで極値を取ります。３つの主慣性モーメントの内２つが、最大および最小の慣性モーメントとなり、残りの１つは最大、最小またはいわゆる鞍点となります。[2]

慣性テンソル

慣性テンソル（inertia tensor）という用語はしばしば慣性行列と同義で使われることがありますが、正確には、慣性テンソルを特定の座標系で表現したものが慣性行列です。一般に、テンソルという量は座標系に依りません。慣性テンソルを図示したものが慣性楕円体です。これは、ベクトルという量が矢印で図示され、ベクトルは座標系に依らないが、座標系を定めればベクトルを成分で表示することができることと似ています。[1]

質量分布に対称性がある場合

質量分布に対称性がある剛体の場合、重心の位置および重心周りの慣性テンソルに関して、いくつかのことがすぐに分かります。

１つの面について対称な場合

一つの面について対称な剛体では、重心は対称面内にあります。この場合、慣性楕円体もこの面について対称ですから、面内に２つの慣性主軸を含みます。従って、３つ目の慣性主軸は対称面に垂直になります。\(z\) 軸を対称面に垂直な軸とすれば、慣性乗積 \(I_{xz}\) と \(I_{yz}\) は \(0\) になります。

直交する２つの面について対称な場合

直交する２つの面について対称な剛体では、重心は交線上にあります。２つの慣性主軸は各面に垂直になります。従って、３つ目の慣性主軸は交線と一致します。

軸対称の場合

軸対称の剛体では、重心は対称軸上にあります。対称軸を交線とするどの２つの直交する平面も対称面となり得ますから、２つの慣性主軸の向きは一意には決まりません。３つ目の慣性主軸は対称軸と一致します。

薄板の直交軸定理

最後に、薄い平板状の剛体において成り立つ便利な定理を紹介します。

下図のように、厚さが無視できる薄い平板に対し、板の面内に \(x\) 軸と \(y\) 軸を取った座標系 \(O-xyz\) を考えます。

質点の座標の \(z\) 成分はすべて \(0\) ですから、座標系 \(O-xyz\) による平板の慣性行列は、式(6)で \(z_i=0\) と置いて、

$$
\begin{align}
\mathbf{I}
& =
\sum_{i} m_i
\begin{bmatrix}
y_i^2 & -x_i y_i & 0 \\
-x_i y_i & x_i^2 & 0 \\
0 & 0 & x_i^2+y_i^2
\end{bmatrix} \tag{27}\\
\end{align}
$$

となります。

慣性行列 \(\mathbf{I}\) を式(8)で表せば、式(27)より、次の関係式が成り立ちます。

$$ I_{zz} = I_{xx} + I_{yy} \tag{28}$$

式(28)は薄板の直交軸定理と呼ばれています。[5]

まとめ

この記事では、剛体の慣性モーメントと慣性行列（慣性テンソル）について詳しく解説しました。ご参考になれば幸いです。

参考文献

[1] 原島鮮.  力学（三訂版）, 裳華房, 1985.

[2] Greenwood, D.T.  Principles of Dynamics. 2nd edition, Prentice Hall, 1988.

[3] 日本機械学会編. マルチボディダイナミクス（1）基礎理論, コンピュータダイナミクスシリーズ3, コロナ社, 2006.

[4] Bretscher, O.  Linear Algebra with Applications, Prentice Hall, 1996.

[5] 日本機械学会編.  機械実用便覧 改訂第7版, 丸善, 2011.