マルチボディダイナミクス超入門

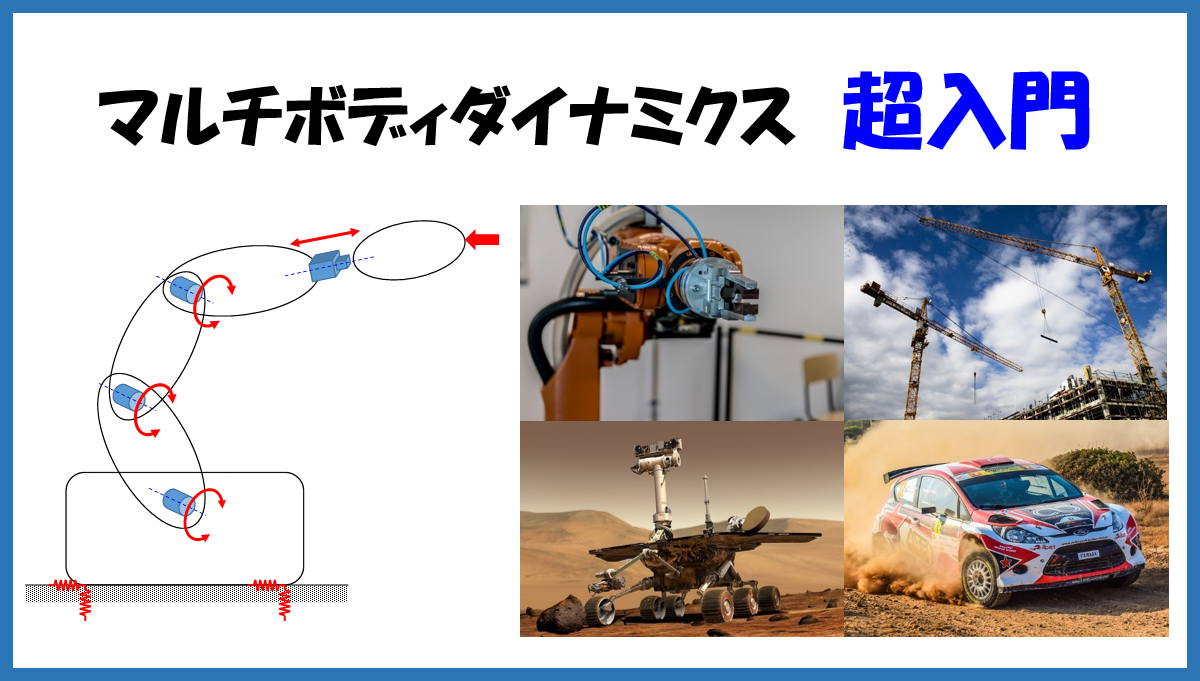
現在、機械システムの解析に広く活用されているマルチボディダイナミクスについて、その定式化と解法の要点を平面（2次元）の剛体マルチボディシステムを例として解説します。

マルチボディダイナミクスとは

マルチボディダイナミクス（多体動力学）とは、多数の物体や部品からなる構造物や機械の運動、振動、制御などを扱う学問です[1]。多数の物体や部品からなる系はマルチボディシステム（多体系）と呼ばれます。

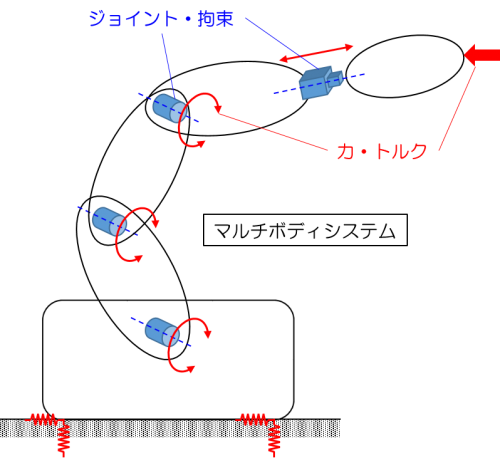
マルチボディダイナミクスの問題には次のような特徴があります。

• 各物体（部品）は大きな並進・回転変位を受ける
• 各物体（部品）の運動は各種ジョイントで拘束される

マルチボディシステムを構成する物体（部品）は剛体として考えることが多いですが、変形が無視できない場合には可変形体として扱うことも可能です。

マルチボディダイナミクスは、例えばロボットアーム、クレーン、宇宙機、自動車など、幅広い機械の運動、振動、制御の解析に応用できます。

この記事では、マルチボディダイナミクスの定式化と解法について、平面（2次元）の剛体マルチボディシステムを例として解説します。

基準枠と物体の座標

下図のような、平面内を運動する物体（剛体）を考えます。

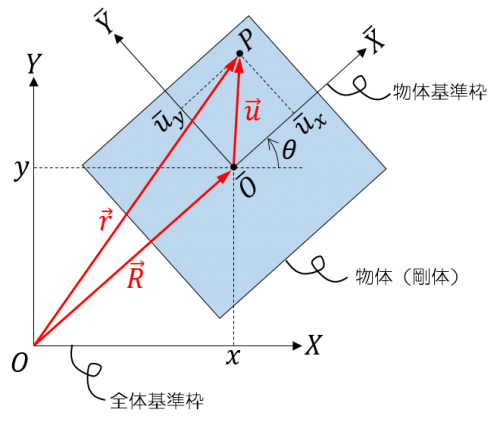
物体の運動を記述するためには、まず基準となる枠（座標系）を定める必要があります。マルチボディダイナミクスでは通常２種類の枠を導入します。一つは慣性系に固定された全体基準枠、もう一つは各物体に固定された物体基準枠です。

物体が剛体の場合には、物体基準枠に対する物体中の各点の位置は不変なので、ある時点における物体の配置は、全体基準枠に対する物体基準枠の位置 \(\mathbf{R}:=\begin{bmatrix}x&y\end{bmatrix}^T\) と回転角 \(\theta\) で完全に特定されます。

物体中の任意の点 \(P\) の物体基準枠による位置座標が \(\bar{\mathbf{u}}:=\begin{bmatrix}\bar{u}_x&\bar{u}_y\end{bmatrix}^T\) であるとき、\(\bar{\mathbf{u}}\) は不変で、点 \(P\) の全体基準枠による位置座標は次式で求められます。

$$
\mathbf{r} =
\mathbf{R}+\mathbf{A}\bar{\mathbf{u}} =
\begin{bmatrix}
x+\bar{u}_x\cos{\theta}-\bar{u}_y\sin{\theta} \\
y+\bar{u}_x\sin{\theta}+\bar{u}_y\cos{\theta}
\end{bmatrix}
\tag{1}
$$

ここで、\(\mathbf{A}\) は物体基準枠の回転行列で

$$
\mathbf{A}:=
\begin{bmatrix}
\cos{\theta} & -\sin{\theta} \\
\sin{\theta} & \cos{\theta}
\end{bmatrix}
\tag{2}
$$

で与えられます。

尚、一般にベクトル \(\vec{a}\) の全体基準枠による成分表示を \(\mathbf{a}\)、物体基準枠による成分表示を \(\bar{\mathbf{a}}\) とすると、

$$ \mathbf{a} = \mathbf{A}\bar{\mathbf{a}} \tag{3} $$

が成り立ちます。ベクトルの成分表示と座標変換については以下の記事で解説しています。

各物体の運動方程式

物体の重心に物体基準枠の原点をとり、物体の質量を \(m\)、重心回りの慣性モーメントを \(J\) とすれば、物体の運動方程式は次式で与えられます。

$$
\begin{cases}
m\ddot{x} = F_x \\
m\ddot{y} = F_y \\
J\ddot{\theta} = T
\end{cases}
\tag{4}
$$

ここで、\( F_x, F_y \) はそれぞれ物体に働く合力の \(X\) 方向成分と \(Y\) 方向成分、\( T \) は物体に働く重心周りのトルクの和です。式(4)は次式のような行列形式で書くことができます。

$$ \mathbf{M}\ddot{\mathbf{q}}=\mathbf{Q} \tag{5} $$

ここで、

$$
\mathbf{M}:=
\begin{bmatrix}
m & 0 & 0 \\
0 & m & 0 \\
0 & 0 & J
\end{bmatrix}, \quad
\mathbf{q}:=\begin{bmatrix} x \\ y \\ \theta \end{bmatrix}, \quad
\mathbf{Q}:=\begin{bmatrix} F_x \\ F_y \\ T \end{bmatrix}
$$

はそれぞれ物体の質量行列、一般化座標ベクトル、一般化力ベクトルと呼ばれます。

ジョイントによる運動学的拘束

マルチボディシステムが \(n_b\) 個の物体で構成されているとき、各物体の一般化座標ベクトルを \(\mathbf{q}^i, i=1,2,\ldots, n_b\) とすれば、マルチボディシステムの一般化座標ベクトルは

$$ \mathbf{q} := \begin{bmatrix} \mathbf{q}^1 \\ \mathbf{q}^2 \\ \vdots \\ \mathbf{q}^{n_b} \end{bmatrix} $$

と書けます。

物体間の各種ジョイントは、物体に対する運動学的な拘束として座標 \(\mathbf{q}\) やその時間微分 \(\dot{\mathbf{q}}\) に関する拘束式で定義されます。特に、座標と時間のみに依存する拘束は、位置拘束または幾何拘束と呼ばれ、

$$ C_j(\mathbf{q}, t) = 0, \quad j = 1, 2, \ldots, n_c \tag{6} $$

の形式で書くことができます。ここで \(n_c\) は拘束式の数です。この記事では位置拘束のみを考え、全拘束式をまとめて

$$
\mathbf{C}(\mathbf{q}, t) :=
\begin{bmatrix} C_1(\mathbf{q}, t) \\ C_2(\mathbf{q}, t) \\ \vdots \\ C_{n_c}(\mathbf{q}, t) \end{bmatrix}
= \mathbf{0} \tag{7}
$$

と書きます。

ジョイントの例

例として2つの代表的なジョイントの拘束式を示します。

回転ジョイント

平面マルチボディシステムにおける回転ジョイントは、2つの物体が1点を共有し、一方の物体が他方の物体に対して共有点周りの回転のみを許される拘束条件です。

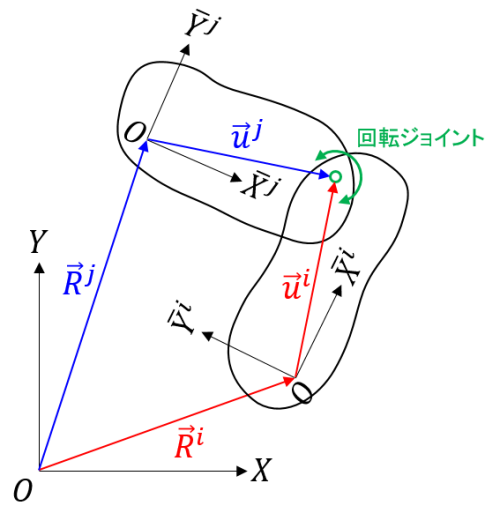
物体 \(i\) と物体 \(j\) を接続する回転ジョイントは、以下のパラメータで特定されます。

• 物体 \(i\) に固定された接続点の位置 \(\bar{\mathbf{u}}^i\)
• 物体 \(j\) に固定された接続点の位置 \(\bar{\mathbf{u}}^j\)

拘束式は式(1)を用いて

$$ (\mathbf{R}^i+\mathbf{A}^i\bar{\mathbf{u}}^i) – (\mathbf{R}^j+\mathbf{A}^j\bar{\mathbf{u}}^j) = \mathbf{0} \tag{8} $$

と書けます。拘束式の数を数える際には、式(8)が2つの独立な式で構成されていることに注意してください。

直動ジョイント

平面マルチボディシステムにおける直動ジョイントは、2つの物体が一つの軸を共有し、一方の物体が他方の物体に対して共通軸方向の並進運動のみを許される拘束条件です。

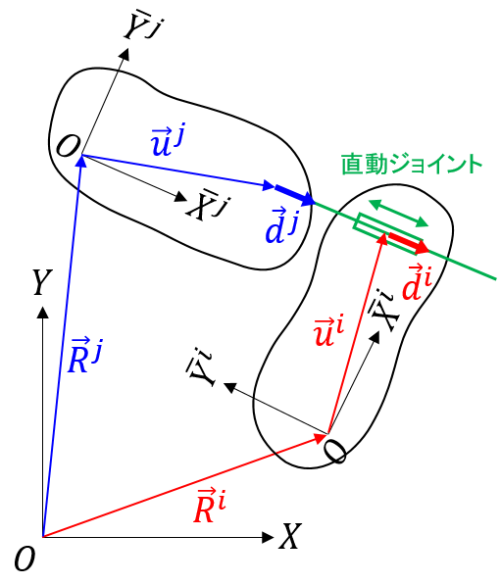
物体 \(i\) と物体 \(j\) を接続する直動ジョイントは、以下のパラメータで特定されます。

• 物体 \(i\) に固定された接続軸上の点の位置 \(\bar{\mathbf{u}}^i\) と軸方向ベクトル \(\bar{\mathbf{d}}^i\)
• 物体 \(j\) に固定された接続軸上の点の位置 \(\bar{\mathbf{u}}^j\) と軸方向ベクトル \(\bar{\mathbf{d}}^j\)

拘束条件を図中の幾何ベクトルで表すと

$$
\begin{cases}
\vec{d}^i \parallel \vec{d}^j \\
(\vec{R}^i+\vec{u}^i) – (\vec{R}^j+\vec{u}^j) \parallel \vec{d}^j
\end{cases}
$$

です。ここで、\(\parallel\) は平行を意味します。上記条件と式(1)と(3)より、拘束式は

$$
\begin{cases}
(\mathbf{A}^i\bar{\mathbf{d}}^i)\times(\mathbf{A}^j\bar{\mathbf{d}}^j) = 0 \\
\{ (\mathbf{R}^i+\mathbf{A}^i\bar{\mathbf{u}}^i) – (\mathbf{R}^j+\mathbf{A}^j\bar{\mathbf{u}}^j) \} \times (\mathbf{A}^j\bar{\mathbf{d}}^j) = 0
\end{cases}
\tag{9}
$$

と書けます。ただし、\(\times\) は外積演算子で、2次元代数ベクトルに対して次のように作用するものとします。

$$ \begin{bmatrix} a_x \\ a_y \end{bmatrix} \times \begin{bmatrix} b_x \\ b_y \end{bmatrix} = a_x b_y – a_y b_x $$

また、式(9)の導出においては、零ベクトルでないベクトル \(\mathbf{a}\) と \(\mathbf{b}\) が平行であることの必要十分条件が \(\mathbf{a}\times\mathbf{b}=0\) であることを利用しています。

ジョイントと自由度

マルチボディシステムの自由度とは、システムに含まれるすべての物体の配置を特定するために必要な、独立な座標の数のことです。一つの平面剛体の自由度は \(3\) ですから、拘束の無い \(n_b\) 個の剛体で構成される平面マルチボディシステムの自由度は \(3n_b\) となります。位置拘束を課すジョイントは独立な座標の数を減らし、従ってシステムの自由度を減らします。一般に、\(n_b\) 個の剛体と \(n_c\) 個の独立な拘束式で構成される平面マルチボディシステムの自由度は

$$ n = 3n_b-n_c $$

となります。

上述の回転ジョイントと直動ジョイントは、それぞれ2個の拘束式で与えられるので、システムにそれらのジョイントを1つ追加するごとに、システムの自由度は \(2\) ずつ減ります。例えば、2個の剛体と2個の独立な回転ジョイントで構成されるマルチボディシステムの自由度は

$$ n = 3\times 2 – (2\times 2) = 2 $$

となります。（本記事最後の例題を参照）

マルチボディシステムの運動方程式

位置拘束を含むマルチボディシステムの運動方程式は、次の微分代数方程式で与えられます。

$$
\begin{cases}
\mathbf{M}\ddot{\mathbf{q}}+\mathbf{C}_{\mathbf{q}}^T\boldsymbol{\lambda} = \mathbf{Q} \\
\mathbf{C}(\mathbf{q}, t) = \mathbf{0}
\end{cases}\tag{10}
$$

ここで、

$$
\mathbf{M}:=
\begin{bmatrix}
\mathbf{M}^1 &  &  & \mathbf{0} \\
& \mathbf{M}^2 &  & \\
&  & \ddots & \\
\mathbf{0} &  &  & \mathbf{M}^{n_b}
\end{bmatrix}, \quad
\mathbf{Q}:=\begin{bmatrix} \mathbf{Q}^1 \\ \mathbf{Q}^2 \\ \vdots \\ \mathbf{Q}^{n_b} \end{bmatrix}
$$

はそれぞれシステムの質量行列と一般化力ベクトルで、\(\mathbf{M}^i\) は各物体の質量行列、\(\mathbf{Q}^i\) は各物体に働く一般化力（拘束力を除く）です。また、

$$
\mathbf{C}_{\mathbf{q}} :=
\begin{bmatrix} \mathbf{C}_{\mathbf{q}^1} & \mathbf{C}_{\mathbf{q}^2} & \cdots & \mathbf{C}_{\mathbf{q}^{n_b}} \end{bmatrix}, \quad
\mathbf{C}_{\mathbf{q}^i} := \frac{\partial\mathbf{C}}{\partial\mathbf{q}^i} =
\begin{bmatrix}
\frac{\partial C_1}{\partial x^i} & \frac{\partial C_1}{\partial y^i} & \frac{\partial C_1}{\partial \theta^i} \\
\frac{\partial C_2}{\partial x^i} & \frac{\partial C_2}{\partial y^i} & \frac{\partial C_2}{\partial \theta^i} \\
\vdots & \vdots & \vdots \\
\frac{\partial C_{n_c}}{\partial x^i} & \frac{\partial C_{n_c}}{\partial y^i} & \frac{\partial C_{n_c}}{\partial \theta^i}
\end{bmatrix}
$$

は拘束ヤコビアン、\(\boldsymbol{\lambda}:=\begin{bmatrix}\lambda_1&\lambda_2&\ldots&\lambda_{n_c}\end{bmatrix}^T\) はラグランジュの未定乗数で、項 \( \mathbf{C}_{\mathbf{q}}^T\boldsymbol{\lambda} \) が拘束力の一般化力に相当します。

数値解析

マルチボディシステムの運動や特性は、式(10)を解析することによって調べることができます。しかし、式(10)を代数的に解くことは通常難しく、多くの場合、コンピュータによる数値解析に頼ることになります。

動力学解析

動力学解析では、所与の初期条件のもとで式(10)を時間積分し、各時点における座標 \(\mathbf{q}(t)\) と速度 \(\dot{\mathbf{q}}(t)\) を求めます。式(10)の微分代数方程式を直接積分する数値計算法も存在しますが、位置拘束式を時間で2回微分して加速度拘束式に変換し、常微分方程式の数値計算法を用いて解くことがよく行われます。そこで、後者の方法を以下で説明します。

拘束式の微分

位置拘束式(7)を時間微分すると、次の速度拘束式を得ます。

$$ \dot{\mathbf{C}} \equiv \mathbf{C}_{\mathbf{q}}\dot{\mathbf{q}} + \mathbf{C}_t = \mathbf{0} \tag{11}$$

速度拘束式(11)をさらに時間微分すると、次の加速度拘束式を得ます。

$$ \ddot{\mathbf{C}} \equiv \mathbf{C}_{\mathbf{q}}\ddot{\mathbf{q}} + \dot{\mathbf{C}}_{\mathbf{q}}\dot{\mathbf{q}} + \dot{\mathbf{C}}_t = \mathbf{0} \tag{12}$$

また式(12)の右側の等式を変形すれば、次式が得られます。

$$
\mathbf{C}_{\mathbf{q}}\ddot{\mathbf{q}} = \boldsymbol{\gamma}, \quad
\boldsymbol{\gamma} := -\dot{\mathbf{C}}_{\mathbf{q}}\dot{\mathbf{q}} – \dot{\mathbf{C}}_t
\tag{13}
$$

式(10)において、位置拘束式を(13)の加速度拘束式で置き換えれば、マルチボディシステムの動力学解析方程式として次式が得られます。

$$
\begin{bmatrix}
\mathbf{M} & \mathbf{C}_{\mathbf{q}}^T \\
\mathbf{C}_{\mathbf{q}} & \mathbf{0}
\end{bmatrix}
\begin{bmatrix} \ddot{\mathbf{q}} \\ \boldsymbol{\lambda} \end{bmatrix} =
\begin{bmatrix} \mathbf{Q} \\ \boldsymbol{\gamma} \end{bmatrix}
\tag{14}
$$

ただし、式(12)または(13)の加速度拘束は位置拘束を保証しない上に動的に不安定であるため、初期状態において位置拘束条件が満たされていたとしても、数値誤差に起因して位置拘束条件が許容差を超えて満たされなくなってしまうことがあります。そこで、式(14)を用いて動力学解析を行う場合には、位置拘束および速度拘束が破綻しないように、次に挙げるような技法がしばしば用いられます。

• 安定化法[3]
• 座標分割法[2]
• 投影法[4]

これらの技法の内、バウムガルテ[3]によって提案された安定化法を簡単に説明します。

バウムガルテ安定化法

上で述べたように、式(12)の加速度拘束式は動的に不安定なので、これを動的に安定な次式で置き換えるのがバウムガルテ安定化法です。

$$ \ddot{\mathbf{C}}+2\alpha\dot{\mathbf{C}}+\beta^2\mathbf{C}=\mathbf{0}, \quad \alpha>0, \beta>0 \tag{15}$$

ここで、\(\alpha, \beta\) は解析対象のマルチボディシステムモデルや常微分方程式の数値計算法の特性に応じて解析者が適宜設定するパラメータです。式(15)に式(12)の左側の等式を代入すれば、

$$ \mathbf{C}_{\mathbf{q}}\ddot{\mathbf{q}} = \boldsymbol{\gamma}-2\alpha\dot{\mathbf{C}}-\beta^2\mathbf{C} \tag{16}$$

を得ます。式(10)において、位置拘束式を式(16)で置き換えれば、マルチボディシステムの動力学解析方程式として式(14)の代わりに次式を得ます。

$$
\begin{bmatrix}
\mathbf{M} & \mathbf{C}_{\mathbf{q}}^T \\
\mathbf{C}_{\mathbf{q}} & \mathbf{0}
\end{bmatrix}
\begin{bmatrix} \ddot{\mathbf{q}} \\ \boldsymbol{\lambda} \end{bmatrix} =
\begin{bmatrix} \mathbf{Q} \\ \boldsymbol{\gamma}-2\alpha\dot{\mathbf{C}}-\beta^2\mathbf{C} \end{bmatrix}
\tag{17}
$$

常微分方程式の数値計算法の適用

一般に、常微分方程式の数値計算法は、次のような形式の初期値問題を解くように設計されています。

$$
\begin{cases}
\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x},t) \\
\mathbf{x}(t_0)=\mathbf{x}_0
\end{cases}
$$

式(17)の動力学解析方程式を解く場合、下の流れ図に示すような常微分方程式関数をプログラムすることにより、上記の初期値問題の形式と合致し、常微分方程式の数値計算法を用いてこれを解くことが可能になります。

静力学解析

静力学解析では、式(10)において速度と加速度をゼロとし、また時間への依存を除去した次式を座標 \(\mathbf{q}\) について解き、マルチボディシステムの静的平衡位置を求めます。

$$
\begin{cases}
\mathbf{C}_{\mathbf{q}}^T\boldsymbol{\lambda} = \mathbf{Q}(\mathbf{q}) \\
\mathbf{C}(\mathbf{q}) = \mathbf{0}
\end{cases}\tag{18}
$$

通常、ニュートン・ラフソン法などの求根アルゴリズムで数値的に(18)の解を求めます。

解析例

例として、下図のようなマルチボディシステムを考えます。

辺の長さが \(2a\)、質量が \(m\) の均質な正方形の剛体が2つ、図のように2つの回転ジョイントと1本のバネダンパで接続され、各物体には負のY方向に重力加速度 \(g\) の重力が働くものとします。

このマルチボディシステムの動力学解析に必要な各物体の質量行列、一般化力ベクトル、拘束式、拘束ヤコビアン、および拘束ヤコビアンの時間微分は以下のように求められます。

物体1の質量行列と一般化力：

$$
\mathbf{M}^1 =
\begin{bmatrix}
m & 0 & 0 \\
0 & m & 0 \\
0 & 0 & \frac{2}{3}m(a)^2
\end{bmatrix}, \quad
\mathbf{Q}^1 = \begin{bmatrix} 0 \\ -mg \\ 0 \end{bmatrix}
$$

物体2の質量行列と一般化力：

$$
\mathbf{M}^2 =
\begin{bmatrix}
m & 0 & 0 \\
0 & m & 0 \\
0 & 0 & \frac{2}{3}m(a)^2
\end{bmatrix}, \quad
\mathbf{Q}^2 = \begin{bmatrix} F_x^{sp} \\ F_y^{sp}-mg \\ T^{sp} \end{bmatrix}
$$

バネダンパの相対変位：

$$
\boldsymbol{\Delta}^{sp} =
\mathbf{R}^2+\mathbf{A}^2\begin{bmatrix}a\\-a\end{bmatrix} – \begin{bmatrix}4a\\0\end{bmatrix} =
\begin{bmatrix}
x^2+a\cos{\theta^2}+a\sin{\theta^2}-4a \\
y^2+a\sin{\theta^2}-a\cos{\theta^2}
\end{bmatrix}
$$

バネダンパの相対速度：

$$
\dot{\boldsymbol{\Delta}}^{sp} =
\begin{bmatrix}
\dot{x}^2-a\dot{\theta^2}(\sin{\theta^2}-\cos{\theta^2}) \\
\dot{y}^2+a\dot{\theta^2}(\cos{\theta^2}+\sin{\theta^2})
\end{bmatrix}
$$

物体2に働くバネダンパの力：

$$
\begin{bmatrix}F_x^{sp}\\F_y^{sp}\end{bmatrix} =
\begin{cases}
-k\boldsymbol{\Delta}^{sp}
-c\left(\frac{\boldsymbol{\Delta}^{sp}}{\left|\boldsymbol{\Delta}^{sp}\right|}\cdot\dot{\boldsymbol{\Delta}}^{sp}\right)
\frac{\boldsymbol{\Delta}^{sp}}{\left|\boldsymbol{\Delta}^{sp}\right|}, \quad \left|\boldsymbol{\Delta}^{sp}\right| \neq 0 \\
-c\dot{\boldsymbol{\Delta}}^{sp}, \quad \left|\boldsymbol{\Delta}^{sp}\right| = 0
\end{cases}
$$

物体2の重心周りに働くバネダンパによるトルク：

$$
T^{sp} =
\left(\mathbf{A}^2\begin{bmatrix}a\\-a\end{bmatrix}\right)
\times
\begin{bmatrix}F_x^{sp}\\F_y^{sp}\end{bmatrix}
= a\{(\cos{\theta^2}+\sin{\theta^2})F_y^{sp}-(\sin{\theta^2}-\cos{\theta^2})F_x^{sp}\}
$$

拘束式：

$$
\begin{align}
\mathbf{C}
&=
\begin{bmatrix}
\mathbf{R}^1+\mathbf{A}^1\begin{bmatrix}-a\\-a\end{bmatrix} \\
\mathbf{R}^1+\mathbf{A}^1\begin{bmatrix}a\\a\end{bmatrix} – \left(\mathbf{R}^2+\mathbf{A}^2\begin{bmatrix}-a\\a\end{bmatrix}\right)
\end{bmatrix} \\
&=
\begin{bmatrix}
x^1-a\cos{\theta^1}+a\sin{\theta^1} \\
y^1-a\sin{\theta^1}-a\cos{\theta^1} \\
x^1+a\cos{\theta^1}-a\sin{\theta^1} – (x^2-a\cos{\theta^2}-a\sin{\theta^2}) \\
y^1+a\sin{\theta^1}+a\cos{\theta^1} – (y^2-a\sin{\theta^2}+a\cos{\theta^2})
\end{bmatrix}
\end{align}
$$

拘束ヤコビアンとその時間微分：

$$
\mathbf{C}_{\mathbf{q}} =
\begin{bmatrix}
1 & 0 & a(\sin{\theta^1}+\cos{\theta^1}) & 0 & 0 & 0 \\
0 & 1 & a(\sin{\theta^1}-\cos{\theta^1}) & 0 & 0 & 0 \\
1 & 0 & -a(\sin{\theta^1}+\cos{\theta^1}) & -1 & 0 & -a(\sin{\theta^2}-\cos{\theta^2}) \\
0 & 1 & -a(\sin{\theta^1}-\cos{\theta^1}) & 0 & -1 & a(\sin{\theta^2}+\cos{\theta^2})
\end{bmatrix}
$$

$$ \mathbf{C}_t =\begin{bmatrix}0 \\ 0 \\ 0 \\ 0\end{bmatrix} $$

$$
\dot{\mathbf{C}}_{\mathbf{q}} =
\begin{bmatrix}
0 & 0 & -a\dot{\theta^1}(\sin{\theta^1}-\cos{\theta^1}) & 0 & 0 & 0 \\
0 & 0 & a\dot{\theta^1}(\sin{\theta^1}+\cos{\theta^1}) & 0 & 0 & 0 \\
0 & 0 & a\dot{\theta^1}(\sin{\theta^1}-\cos{\theta^1}) & 0 & 0 & -a\dot{\theta^2}(\sin{\theta^2}+\cos{\theta^2}) \\
0 & 0 & -a\dot{\theta^1}(\sin{\theta^1}+\cos{\theta^1}) & 0 & 0 & -a\dot{\theta^2}(\sin{\theta^2}-\cos{\theta^2})
\end{bmatrix}
$$

$$ \dot{\mathbf{C}}_t =\begin{bmatrix}0 \\ 0 \\ 0 \\ 0\end{bmatrix} $$

パラメータ値と初期条件を次のように設定して動力学解析を行ってみます。

パラメータ：

$$ \begin{cases} g = 9.81 [m/s^2] \\ m = 5 [kg] \\ a = 1 [m] \\ k = 10 [N/m] \\ c = 1 [Ns/m] \end{cases} $$

初期条件：

$$ \begin{bmatrix} x^1(0) \\ y^1(0) \\ \theta^1(0) \end{bmatrix} = \begin{bmatrix} a \\ a \\ 0 \end{bmatrix}, \quad \begin{bmatrix} \dot{x}^1(0) \\ \dot{y}^1(0) \\ \dot{\theta}^1(0) \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix} $$

$$ \begin{bmatrix} x^2(0) \\ y^2(0) \\ \theta^2(0) \end{bmatrix} = \begin{bmatrix} 3a \\ a \\ 0 \end{bmatrix}, \quad \begin{bmatrix} \dot{x}^2(0) \\ \dot{y}^2(0) \\ \dot{\theta}^2(0) \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix} $$

下図は動力学解析結果のアニメーションです。

まとめ

この記事では、マルチボディダイナミクスの定式化と解法について、平面（2次元）の剛体マルチボディシステムを例として解説しました。現在、マルチボディダイナミクスの解析を手軽に行えるソフトウェアが多数存在します。それらのソフトウェアを利用する場合に、背後にある理論や解法をある程度理解しておくことは、正しく効果的な解析を行うために重要ではないかと思います。また、理論や解法を理解すれば、解析プログラムを自作することも可能です。マルチボディダイナミクスの理論についてさらに知識を深めたい方は、参考文献[1]や[2]をあたってみてください。マルチボディダイナミクスの応用に興味のある方は、参考文献[5]などが参考になると思います。

参考文献

[1] 日本機械学会編. マルチボディダイナミクス（1）基礎理論, コンピュータダイナミクスシリーズ3, コロナ社, 2006.

[2] Shabana, A. A. Dynamics of Multibody Systems. 4th edition, Cambridge, 2013.

[3] Baumgarte, J. “Stabilization of Constraints and Integrals of Motion in Dynamical Systems,” Computer Methods in Applied Mechanics and Engineering 1 (1972), 1-16.

[4] Ascher, U. M.; Chin, H.; Petzold, L. R.; Reich, S. “Stabilization of Constrained Mechanical Systems with DAEs and Invariant Manifolds,” Mechanics Based Design of Structures and Machines 23 (1995), 2, p.135-157.

[5] Blundell, M.; Harty, D. “The Multibody Systems Approach to Vehicle Dynamics,” Elsevier, 2004.