オイラーの運動方程式は、剛体の角速度ベクトルの時間変化を記述する常微分方程式で、剛体の回転運動を支配しています。並進運動を司るニュートンの運動方程式と組み合わせて、剛体の運動を解析する際によく用いられます。この記事では、一般的な質点系の回転運動方程式からオイラーの運動方程式を、行列形式の簡潔な式を用いて導出する方法を解説します。導出の過程では、剛体の慣性行列やその座標変換などの概念も説明します。
予備知識
この記事では、以下の関連記事で解説した概念や結果を利用しています。必要に応じて参照してください。
回転する剛体と参照枠の定義
下図のように、慣性系に固定された枠(慣性枠)に対して回転運動する剛体を考えます。剛体中の慣性系に固定された点または剛体の重心を \(O\) とし、慣性枠に平行な枠 \(O-xyz\) と、剛体に固定された枠(剛体枠)\(O-x^\prime y^\prime z^\prime\) を考えます。
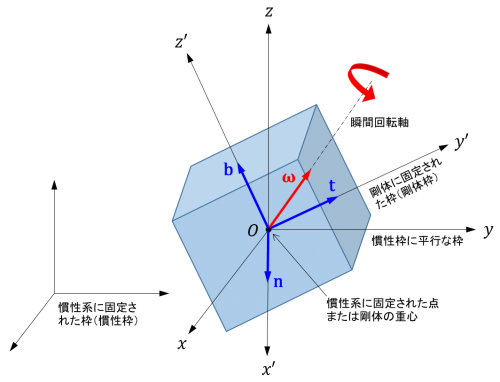
この記事では、すべてのベクトルを成分表示の代数ベクトルで表し、ある幾何ベクトル \(\vec{a}\) の慣性枠(または慣性枠に平行な枠 \(O-xyz\))による成分表示を \(\mathbf{a}\)、剛体枠 \(O-x^\prime y^\prime z^\prime\) による成分表示を \(\mathbf{a}^\prime\) と書きます。
慣性枠に対する剛体枠の回転行列を \(\mathbf{R}\equiv\begin{bmatrix} \mathbf{n} & \mathbf{t} & \mathbf{b}\end{bmatrix}\)、剛体の角速度ベクトルを \(\boldsymbol{\omega}\) とします。(\(\mathbf{n}\)、\(\mathbf{t}\)、\(\mathbf{b}\) はそれぞれ \(x^\prime\)、\(y^\prime\)、\(z^\prime\) 軸方向の単位ベクトルです。)
質点系の回転運動方程式
剛体は質点系の特殊な場合ですから、質点系の運動方程式が適用できます。点 \(O\) 周りの角運動量を \(\mathbf{H}\)、力のモーメントを \(\mathbf{M}\) とすると、質点系の回転運動方程式は
$$
\dot{\mathbf{H}} = \mathbf{M} \tag{1}
$$
で与えられます。ドット記号は時間微分を表します(\(\dot{\mathbf{a}}\equiv\frac{d}{dt}\mathbf{a}\))。
角運動量 \(\mathbf{H}\) は各質点の点 \(O\) 周りの角運動量の総和として定義されます。
$$
\begin{align}
\mathbf{H}
& \equiv \sum_{i} \boldsymbol{\rho}_i \times m_i\dot{\boldsymbol{\rho}}_i \\
& = \sum_{i} m_i\tilde{\boldsymbol{\rho}}_i\dot{\boldsymbol{\rho}}_i \tag{2} \\
\end{align}
$$
ここで、\(m_i\) は質点 \(i\) の質量、\(\boldsymbol{\rho}_i\) は質点 \(i\) の点 \(O\) に対する位置ベクトルです。また、\(\tilde{\boldsymbol{\rho}}_i\) は \(\boldsymbol{\rho}_i\) のチルダ行列を表します。
剛体の角運動量
質点 \(i\) の位置ベクトル \(\boldsymbol{\rho}_i\) の 剛体枠による成分表示を \(\boldsymbol{\rho}_i^\prime\) とすると、
$$ \boldsymbol{\rho}_i = \mathbf{R}\boldsymbol{\rho}_i^\prime \tag{3}$$
の関係があります。剛体の場合、\(\boldsymbol{\rho}_i^\prime\) は一定です。式(3)を時間微分して、回転行列の時間微分の公式
$$ \dot{\mathbf{R}}=\tilde{\boldsymbol{\omega}}\mathbf{R} \tag{4}$$
を適用すれば、
$$
\begin{align}
\dot{\boldsymbol{\rho}}_i
& = \dot{\mathbf{R}}\boldsymbol{\rho}_i^\prime \\
& = \tilde{\boldsymbol{\omega}}\mathbf{R}\boldsymbol{\rho}_i^\prime \\
& = \tilde{\boldsymbol{\omega}}\boldsymbol{\rho}_i \\
& = \boldsymbol{\omega}\times\boldsymbol{\rho}_i \\
& = -\boldsymbol{\rho}_i\times\boldsymbol{\omega} \\
& = -\tilde{\boldsymbol{\rho}}_i\boldsymbol{\omega} \tag{5}\\
\end{align}
$$
を得ます。
式(5)を式(2)へ代入すると、
$$
\mathbf{H} =
\left[-\sum_{i} m_i \tilde{\boldsymbol{\rho}}_i \tilde{\boldsymbol{\rho}}_i \right]\boldsymbol{\omega} \tag{6} \\
$$
となり、ここで、
$$
\mathbf{I} \equiv -\sum_{i} m_i \tilde{\boldsymbol{\rho}}_i \tilde{\boldsymbol{\rho}}_i \tag{7}
$$
と置けば、式(6)より、剛体の角運動量を
$$
\mathbf{H}=\mathbf{I}\boldsymbol{\omega} \tag{8} \\
$$
と表すことができます。行列 \(\mathbf{I}\) は剛体の慣性行列と呼ばれるものです。
剛体の慣性行列
離散的に質量が分布している場合
質点 \(i\) の位置ベクトルの成分を \(\boldsymbol{\rho}_i = [x_i, y_i, z_i]^T\) とすれば、慣性行列は次のように表せます。
$$
\begin{align}
\mathbf{I}
& \equiv
-\sum_{i} m_i \tilde{\boldsymbol{\rho}}_i \tilde{\boldsymbol{\rho}}_i \\
& =
-\sum_{i} m_i
\begin{bmatrix}
0 & -z_i & y_i \\
z_i & 0 & -x_i \\
-y_i & x_i & 0
\end{bmatrix}
\begin{bmatrix}
0 & -z_i & y_i \\
z_i & 0 & -x_i \\
-y_i & x_i & 0
\end{bmatrix} \\
& =
\sum_{i} m_i
\begin{bmatrix}
y_i^2+z_i^2 & -x_i y_i & -x_i z_i \\
-x_i y_i & x_i^2+z_i^2 & -y_i z_i \\
-x_i z_i & -y_i z_i & x_i^2+y_i^2
\end{bmatrix} \tag{9}\\
\end{align}
$$
式(9)から、慣性行列 \(\mathbf{I}\) は対称行列であることが分かります。
連続的に質量が分布している場合
連続的に質量が分布している剛体の場合、剛体の質量密度を \(\rho\) とすると、式(7)において、質点 \(m_i\) を質量 \(\rho dV\) の微小体積要素 \(dV\) に置き換え、和を剛体の体積全体についてとれば、慣性行列は次の体積積分になります。
$$
\begin{align}
\mathbf{I}
& =
-\int_{V} \rho\tilde{\boldsymbol{\rho}}\tilde{\boldsymbol{\rho}} \: dV \\
& =
-\int_{V} \rho
\begin{bmatrix}
0 & -z & y \\
z & 0 & -x \\
-y & x & 0
\end{bmatrix}
\begin{bmatrix}
0 & -z & y \\
z & 0 & -x \\
-y & x & 0
\end{bmatrix}
dV \\
& =
\int_{V} \rho
\begin{bmatrix}
y^2+z^2 & -xy & -xz \\
-xy & x^2+z^2 & -yz \\
-xz & -yz & x^2+y^2
\end{bmatrix}
dV \tag{10}\\
\end{align}
$$
慣性行列の座標変換
慣性行列は座標系に依存します。式(7)の慣性行列 \(\mathbf{I}\) は、慣性枠に平行な枠 \(O-xyz\) を基準としたものです。一方、剛体枠 \(O-x^\prime y^\prime z^\prime\) を基準とした慣性行列は次式で定義されます。
$$
\mathbf{I}^\prime \equiv -\sum_{i} m_i \tilde{\boldsymbol{\rho}_i^\prime} \tilde{\boldsymbol{\rho}_i^\prime} \tag{11}
$$
では、\(\mathbf{I}\) と \(\mathbf{I}^\prime\) の関係はどうなっているのでしょうか。
「ベクトルの成分表示と座標変換」の記事で示したように、式(3)の関係を持つ \(\boldsymbol{\rho}_i\) と \(\boldsymbol{\rho}_i^\prime\) のチルダ行列 \(\tilde{\boldsymbol{\rho}_i}\) と \(\tilde{\boldsymbol{\rho}_i^\prime}\) の間には次の関係があります。
$$
\tilde{\boldsymbol{\rho}_i} = \mathbf{R}\tilde{\boldsymbol{\rho}_i^\prime}\mathbf{R}^T \tag{12}
$$
式(7)に(12)を代入して、回転行列 \(\mathbf{R}\) が直交行列である(\(\mathbf{R}^{-1}=\mathbf{R}^T\) である)ことを考慮すれば、
$$
\begin{align}
\mathbf{I}
& =
-\sum_{i} m_i\tilde{\boldsymbol{\rho}}_i\tilde{\boldsymbol{\rho}}_i \\
& =
-\sum_{i} m_i
(\mathbf{R}\tilde{\boldsymbol{\rho}_i^\prime}\mathbf{R}^T)
(\mathbf{R}\tilde{\boldsymbol{\rho}_i^\prime}\mathbf{R}^T) \\
& =
\mathbf{R}
\left[-\sum_{i} m_i\tilde{\boldsymbol{\rho}_i^\prime}\tilde{\boldsymbol{\rho}_i^\prime} \right]
\mathbf{R}^T \\
\end{align}
$$
となりますから、これに式(11)を代入して
$$ \mathbf{I}=\mathbf{R} \mathbf{I}^\prime \mathbf{R}^T \tag{13}$$
を得ます。これは慣性行列の座標変換の式です。また、式(13)の両辺に左から \(\mathbf{R}^T\)、右から \(\mathbf{R}\) を乗ずれば、逆変換の式
$$ \mathbf{I}^\prime=\mathbf{R}^T \mathbf{I} \mathbf{R} \tag{14}$$
が得られます。
慣性行列の時間微分
枠 \(O-xyz\) に対して剛体は回転運動しているので、質点の位置ベクトル \(\boldsymbol{\rho}_i\) は時間によって変化します。従って、式(3)で定義される枠 \(O-xyz\) による慣性行列 \(\mathbf{I}\) は時間によって変化します。
一方、剛体枠 \(O-x^\prime y^\prime z^\prime\) による質点の位置ベクトルの成分表示 \(\boldsymbol{\rho}_i^\prime\) は一定ですから、式(11)で定義される剛体枠による慣性行列 \(\mathbf{I}^\prime\) は一定で時間によって変化しません。
オイラーの方程式を導くための最後の準備として、慣性行列 \(\mathbf{I}\) の時間微分を求めましょう。
式(13)を時間微分して、式(4)の回転行列の時間微分の公式を用いれば、次の結果が得られます。
$$
\begin{align}
\dot{\mathbf{I}}
& =
\dot{\mathbf{R}}\mathbf{I}^\prime\mathbf{R}^T + \mathbf{R}\mathbf{I}^\prime\dot{\mathbf{R}}^T \\
& =
\tilde{\boldsymbol{\omega}}\mathbf{R}\mathbf{I}^\prime\mathbf{R}^T
+ \mathbf{R}\mathbf{I}^\prime\mathbf{R}^T\tilde{\boldsymbol{\omega}}^T \\
& =
\tilde{\boldsymbol{\omega}}\mathbf{I}+\mathbf{I}\tilde{\boldsymbol{\omega}}^T \\
& =
\tilde{\boldsymbol{\omega}}\mathbf{I}-\mathbf{I}\tilde{\boldsymbol{\omega}} \tag{15}\\
\end{align}
$$
ここで、最後の等号はチルダ行列が歪対称行列であることを用いました。(\(\tilde{\boldsymbol{\omega}}^T=-\tilde{\boldsymbol{\omega}}\))
オイラーの運動方程式(枠 \(O-xyz\) による表現)
では、いよいよオイラーの運動方程式を導きます。
式(8)を時間微分し、式(15)を用いれば、角運動量の時間微分は、
$$
\begin{align}
\dot{\mathbf{H}}
& =
\dot{\mathbf{I}}\boldsymbol{\omega}+\mathbf{I}\dot{\boldsymbol{\omega}} \\
& =
(\tilde{\boldsymbol{\omega}}\mathbf{I}-\mathbf{I}\tilde{\boldsymbol{\omega}})\boldsymbol{\omega}+\mathbf{I}\dot{\boldsymbol{\omega}} \\
& =
\tilde{\boldsymbol{\omega}}\mathbf{I}\boldsymbol{\omega}+\mathbf{I}\dot{\boldsymbol{\omega}} \tag{16}\\
\end{align}
$$
となります。ここで最後の等号は、自身の外積が零ベクトルであることを用いています。
$$
\tilde{\boldsymbol{\omega}}\boldsymbol{\omega} = \boldsymbol{\omega}\times\boldsymbol{\omega} = \mathbf{0}
$$
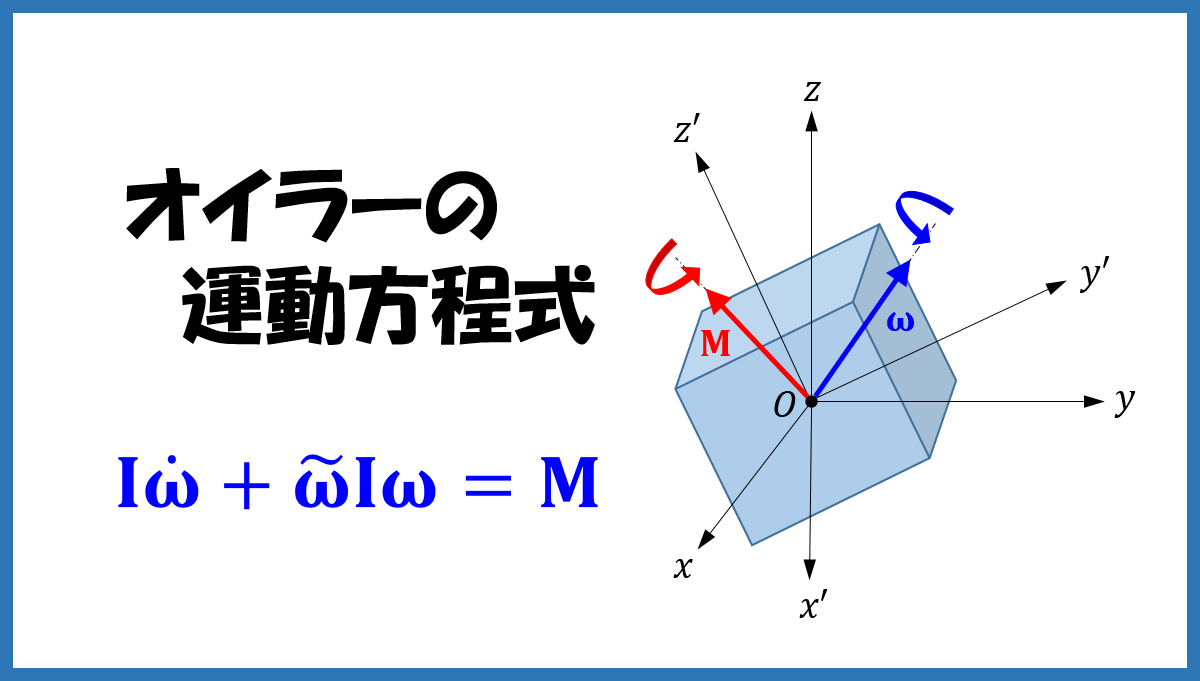
式(16)を式(1)へ代入すれば、以下の回転運動方程式が得られます。
$$
\mathbf{I}\dot{\boldsymbol{\omega}}+\tilde{\boldsymbol{\omega}}\mathbf{I}\boldsymbol{\omega}=\mathbf{M} \tag{17}
$$
式(17)は、枠 \(O-xyz\) によるオイラーの運動方程式の表現です。
オイラーの運動方程式(剛体枠による表現)
式(17)は、慣性行列 \(\mathbf{I}\) が時間によって変化するので使いにくい場合もあります。そこで、式(17)を座標変換して、剛体枠による表現を求めてみましょう。
一般の場合
角速度ベクトルとそのチルダ行列の座標変換は、それぞれ以下の式(18)と(19)で与えられます。
$$
\boldsymbol{\omega} = \mathbf{R}\boldsymbol{\omega}^\prime \tag{18}
$$
$$
\tilde{\boldsymbol{\omega}} = \mathbf{R}\tilde{\boldsymbol{\omega}^\prime}\mathbf{R}^T \tag{19}
$$
式(18)を時間微分すれば
$$
\begin{align}
\dot{\boldsymbol{\omega}}
& =
\dot{\mathbf{R}}\boldsymbol{\omega}^\prime+\mathbf{R}\dot{\boldsymbol{\omega}}^\prime \\
& =
\mathbf{R}\tilde{\boldsymbol{\omega}^\prime}\boldsymbol{\omega}^\prime+\mathbf{R}\dot{\boldsymbol{\omega}}^\prime \\
& =
\mathbf{R}\dot{\boldsymbol{\omega}}^\prime \tag{20} \\
\end{align}
$$
を得ます。式(17)に式(18)(19)(20)を代入すると
$$
\mathbf{I}(\mathbf{R}\dot{\boldsymbol{\omega}}^\prime)+(\mathbf{R}\tilde{\boldsymbol{\omega}^\prime}\mathbf{R}^T)\mathbf{I}(\mathbf{R}\boldsymbol{\omega}^\prime)=\mathbf{M}
$$
また、左から \(\mathbf{R}^T\) を掛けると
$$
(\mathbf{R}^T\mathbf{I}\mathbf{R})\dot{\boldsymbol{\omega}}^\prime+\tilde{\boldsymbol{\omega}^\prime}(\mathbf{R}^T\mathbf{I}\mathbf{R})\boldsymbol{\omega}^\prime=\mathbf{R}^T\mathbf{M}
$$
さらに、式(13)と \(\mathbf{R}^T\mathbf{M}=\mathbf{M}^\prime\) を代入すれば
$$
\mathbf{I}^\prime\dot{\boldsymbol{\omega}}^\prime
+ \tilde{\boldsymbol{\omega}^\prime}\mathbf{I}^\prime\boldsymbol{\omega}^\prime
= \mathbf{M}^\prime \tag{21}
$$
を得ます。式(21)は剛体枠 \(O-x^\prime y^\prime z^\prime\) によるオイラーの方程式の表現です。式(17)と式(21)は形は全く同じですが、式(21)の慣性行列 \(\mathbf{I}^\prime\) は一定です。
剛体枠を慣性主軸に一致させた場合
剛体枠 \(O-x^\prime y^\prime z^\prime\) の選び方によっては、剛体枠による慣性行列 \(\mathbf{I}^\prime\) が対角行列になります。慣性行列 \(\mathbf{I}^\prime\) が対角行列になるとき、\(x^\prime\)軸、\(y^\prime\)軸、および\(z^\prime\) 軸は慣性主軸と呼ばれる軸と一致しています。このとき、
$$
\mathbf{I}^\prime =
\begin{bmatrix}
I_{xx}^\prime & 0 & 0 \\
0 & I_{yy}^\prime & 0 \\
0 & 0 & I_{zz}^\prime \\
\end{bmatrix}, \quad
\boldsymbol{\omega}^\prime =
\begin{bmatrix}
\omega_x^\prime \\ \omega_y^\prime \\ \omega_z^\prime \\
\end{bmatrix}, \quad
\mathbf{M}^\prime =
\begin{bmatrix}
M_x^\prime \\ M_y^\prime \\ M_z^\prime \\
\end{bmatrix}
$$
と置けば、式(21)は
$$
\begin{align}
I_{xx}^{\prime}\dot{\omega}_x^\prime+(I_{zz}^\prime-I_{yy}^\prime)\omega_y^\prime\omega_z^\prime & = M_x^\prime \\
I_{yy}^{\prime}\dot{\omega}_y^\prime+(I_{xx}^\prime-I_{zz}^\prime)\omega_z^\prime\omega_x^\prime & = M_y^\prime \\
I_{zz}^{\prime}\dot{\omega}_z^\prime+(I_{yy}^\prime-I_{xx}^\prime)\omega_x^\prime\omega_y^\prime & = M_z^\prime \\
\end{align}
$$
と書けます。
まとめ
この記事では、一般的な質点系の回転運動方程式からオイラーの運動方程式を、行列形式の簡潔な式表現を用いて導出する方法を解説しました。また、剛体の慣性行列やその座標変換などの概念も合わせて説明しました。
オイラーの運動方程式を用いれば、剛体の回転運動をシミュレーションすることができます。下の関連記事では、オイラーの運動方程式を用いた独楽(こま)のシミュレーションの例題を扱っていますので、よろしければご覧ください。
最後まで読んでいただきありがとうございました。この記事がご参考になれば幸いです。






コメント
すみません。物理を理解したいのですが、理系音痴で私の間違った理解をここに書いてしまうかもしれません。
このコメントをお読みの一般の読者の方は、そのことをご了承下さい。
本題
本テーマで、はじめに基準座標系と平行な、剛体座標系と原点を共有する空間に固定された慣性座標系が設定されてるかと思います。
剛体は特定の固定軸周りではなく、任意の回転を基準座標系、ないし慣性座標系に対して行い、それが瞬間回転軸として与えられてるかと思います。
素朴な疑問なのですが、剛体は基準座標系に対してωで回転する訳ですから、剛体座標系の原点の基準座標系に対する位置ベクトルは時間とともに変化しますよね?
ということは、慣性座標系の原点も、剛体座標系の原点と一致するように取ると思うのですが(この理解を間違ってたらすみません。)この原点は基準座標系に対して時間とともに運動することになりますか?
つまり、はじめに与えられた図は、何かしらの瞬間に着目した関係であり、別の時刻の剛体座標系(並びに慣性座標系)の原点までの位置ベクトルはまた他の位置に来るのでしょうか?
また、剛体は基準座標系に対して回転運動だけを想定していますか?並進運動も同時に想定されてますか?
どうぞ、よろしくお願いします。
ご質問ありがとうございます。
座標系O-xyzは、慣性座標系に平行な(慣性系に対して回転しない)座標系であり、それ自体が慣性座標系である必要はありません。点Oを剛体の重心とし、剛体が任意の運動をする場合には、座標系O-xyzは剛体の重心とともに並進運動します。